集成正态云和动态扰动的哈里斯鹰优化算法(IHHO)

摘要： 针对基本哈里斯鹰算法收敛速度慢和易陷入局部寻优等问题，提出一种集成正态云模型和动态扰动策略的改进哈里斯鹰算法。在全局搜索阶段，利用正态云模型的随机性和模糊性和随机反向学习思想对哈里斯鹰位置进行更新，从而丰富种群多样性和提高算法全局搜索能力。在局部开发阶段，引入动态扰动策略更新不同捕食策略下的哈里斯鹰位置，改善算法局部开发能力。

1.哈里斯鹰优化算法

基础哈里斯鹰优化算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/108528147

2.改进哈里斯鹰优化算法

2.1 正态云模型

云模型由期望 $Ex、$ 、熵 $En$ 和超熵 $He$ 三个参数进行描述, 当 $En$ 增大时, 云滴分布范围随之变大, 当 $He$ 增 大时, 云滴的离散程度同步增大, 侧面反映云滴分布的随机 性和模糊性。正向正态云发生器是产生基本服从正态分布云 滴的一种算法, 通过设定的参数来产生云滴, 直到生成期望 的云滴数量。正态云滴生成过程可定义为如下所示 ${}^{[12]}$ :
$$\mathbf{X}\left[x_1,x_2,\cdots x_{Nd}\right]=\mathrm{Gnc}(Ex,En,He,Nd)\text{\hspace{1em}(12)}$$
其中: $Nd$ 为期望云滴个数。

本文引入正态云模型作为哈里斯鹰位置新的更新机制。 通过正态云模型的期望值 $Ex$ 对最优位置解进行开发, 通过 $En$ 调控其余位置解, 利用 $\mathrm{He}$ 调整哈里斯鹰位置离散程度, 公式如下所示 ${}^{[13]}$ :
$${\text{ Position }}^{\prime }=\mathrm{Gnc}({\text{ Position }}_{\text{best }},\text{ En, He, Nd) }\text{\hspace{1em}(13)}$$

$$En=\lambda \times {\left(\frac{T-t}{T}\right)}^{\tau }\text{\hspace{1em}(14)}$$

$$\begin{array}{c}He=En\times 10^{-\xi }\end{array}\text{\hspace{1em}(15)}$$

2.2 随机反向学习思想

反向学习思想自被提出以来, 就成为优化算法常用的一 种改进策略, 主要是通过对算法可行解进行反向学习, 通过 评估原始解和反向解, 选取更优解加入算法迭代。为此, 本 文引入随机反向学习思想对最差哈里斯鹰位置进行更新 ${}^{[14]}$, 公式如下所示:
$${\mathbf{X}}_{\text{worst },t+1}=u{b}_1+\mathrm{rand}\times \left(l{b}_1-{\mathbf{X}}_{worst,t}\right)\text{\hspace{1em}(16)}$$
其中: ${\mathbf{X}}_{worst}$ 表示最差哈里斯鹰位置, $u{b}_1$ 和 $l{b}_1$ 分别为 动态边界的上下界。
随着算法迭代, 通过式 (16) 对位置最差值进行更新, 得到反向随机解, 从而提高哈里斯鹰种群多样性和寻得全局 最优解几率。同时随机反向学习采用动态边界 $u{b}_1$ 和 $l{b}_1$, 降 低了传统的固定边界 $ub$ 和 $lb$ 易丢失搜索信息的问题, 也降低了改进算法的计算复杂度。

2.3 动态扰动策略

当猎物能量 $|E|<1$ 时, 算法进入开发阶段, 但无法保 证此时种群都接近全局最优, 可能会导致收玫太早以及陷入 局部寻优。因此, 在 4 种捕食策略 中引入了一种动态扰动策略, 在保证算法寻优精度的基础上 能迅速跳出局部寻优。
$$\psi =-\cos \left(\frac{\pi t}{2T}+\pi \right)\text{\hspace{1em}(17)}$$

$$\begin{array}{c}{\mathbf{X}}_{\psi ,\text{ rabbit }}=\psi \times {\mathbf{X}}_{\text{rabbit }}\end{array}\text{\hspace{1em}(18)}$$
其中: $\psi$ 为扰动系数; ${\mathbf{X}}_{\psi ,\text{ rabbit }}$ 为加入扰动后的猎物位置。

流程图如下：

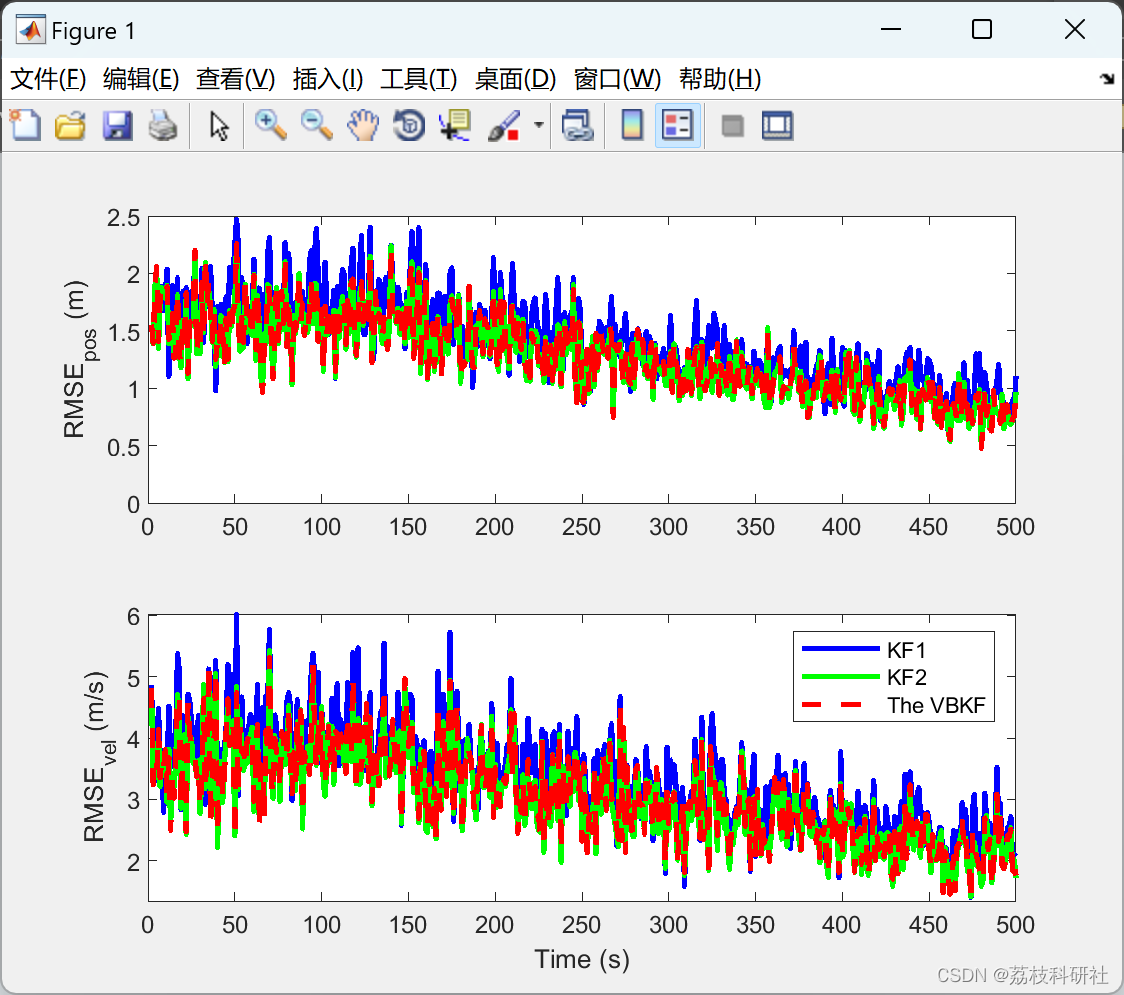
3.实验结果

4.参考文献

[1]张帅,王俊杰,李爱莲,全凌翔,崔桂梅.集成正态云和动态扰动的哈里斯鹰优化算法[J/OL].小型微型计算机系统:1-11[2023-06-06].DOI:10.20009/j.cnki.21-1106/TP.2021-0791.

5.Matlab代码

6.python代码