目录

1.算法描述

2.仿真效果预览

3.MATLAB核心程序

4.完整MATLAB

---

1.算法描述

        电力工业是当今世界各国经济的重要组成部分，随着世界经济的不断发展，电网的建设和中长期规划和经济发展之间的矛盾变得越来越突出，对电力系统的需求也变得越来越大。在实际的电网建设过程中，合理的中长期的电网规划对整个区域的经济发展起到至关重要的作用。而不合理的规划不仅会增加建设成本，而且会影响整个电网运行的稳定性和可靠性。 介绍了常见的优化算法，包括线性规划，粒子群优化算法以及遗传优化算法，并提出了一种基于自适应交叉变异的遗传优化算法，使得选择的精英个体数量和参与变异的个体数量之间的比例达到最优。通过这种改进遗传优化算法可以有效解决传统优化算法所存在的局部优化问题。然后提出了一种投资费用和网络损耗费用最小化的电网规划数学模型，并将直流潮流，支路容量，决策变量取值范围以及电压降作为约束条件。最后将优化算法应用到电网规划中，通过 IEEE-6节点系统为例并通过MATLAB进行仿真计算和分析，从而证明算法在电网规划应用中的可行性。

        遗传算法 (Genetic Algorithm，GA) 是一种基于规律进化的随机优化搜索算法，该算法最早是由Holland在1975年提出的。遗传算法的主要优势是通过对目标对象进行优化操作，并通过基于概率的搜索方法，获得相应的搜索空间，因此GA算法具有较强的全局搜索能力。由于遗传算法特有的全局搜索能力，其被广泛使用在各个领域，包括信号处理，机器学习以及控制域等。遗传优化的主要算法流程图如下图所示：

        在一个中长期电网规划中，需要考虑的目标函数可以认为是新建电网线路的投资年费用和电网系统的运行费用之和的最小值，满足这目标值最小且符合电网运行的约束要求即是求解问题的最优解。根据这个原理，首先给出任意一年的目标函数为：

        遗传优化算法是一种基于全局最优解搜索算法，而电网规划的优化是一个较为复杂的优化设计过程。因此，采用遗传算法对电网规划进行优化设计是一个较好的解决方案。遗传优化算法主要步骤包括编码、选择、交叉以及变异等步骤，下面将基于遗传优化算法的基本实现过程对电网规划的优化设计进行实现。

        第一，编码实现。在遗传优化算法中，需要通过二进制编码实现对染色体的编码，对于电网规划问题，编码方式是通过1和0分别表示待选线路是否加入到电网系统中，假设某一电网系统中有8条待选线路，其染色体编码结果为{01100010}，则说明编号为2，3，7的待选线路将加入到电网系统中。

        第二、遗传算法的初始种群规模的确定。遗传算法中的种群规模对算法的最优解计算能力有着较大的影响，当遗传算法的种群规模较大的时候，种群中的每一个个体可能具有的个体多样性概率越高，那么算法就越有可能找到实际的最优解，但这是以增加计算量为代价的。而当种群规模较小的时候，那么种群中每一个个体可能具有的个体多样性概率就月底，那么就会导致算法陷入局部优化的困境。因此，需要通过不断的仿真验证来获得最优的初始种群规模。

        第四、选择算子的确立。遗传优化算法的选择操作，其主要功能是根据个体适应度值来选择当前个体在后代中得到繁衍的机会。通过选择操作不仅可以保证种群的多样性，还反应了遗传算法的适者生存的原则。这里根据公式2.10的公式，采取基于排序选择的方法进行选择性操作。

        第五、交叉算子的确立。对于遗传算法的交叉方式的确定，主要涉及到遗传优化过程的全局最优解搜索能力。种群中的每一个个体通过交叉操作，使得染色体产生两个新的个体，其反应了两种新的不同的电网规划优化设计方案。其中，个体交叉操作是以一定的概率进行操作的，即交叉概率。交叉概率对交叉操作有着较大的影响，当交叉概率较大的时候，有利于遗传算法对新的搜索区域进行搜索，但是过多的交叉操作，会使得优秀的基因被破坏，从而降低全局搜索能力。当交叉概率较小的时候，表面大量的父代信息直接遗传给子代，使得部分子代个体出现早熟的问题。因此，在本课题中，遗传算法的交叉概率通过自适应调整的方式来进行交叉操作。

        第六、变异算子的确立。在完成交叉处理之后，进行变异操作，变异的含义是生成与两个父代个体特性相接近的新的子代个体，即产生了两个新的电网规划方案，此时，将两个新的电网规划方案和旧方案进行比较，将其中性能较好的方案进行保留。特别是在遗传算法迭代后期，由于通过大量的交叉操作之后，种群的的各个个体之间存在较大的相似性，丧失了多样式，使得遗传优化停滞不前，因此需要通过变异操作，增加个体的多样性。从而使算法具有全局最优性，进一步增强了GA的能力。

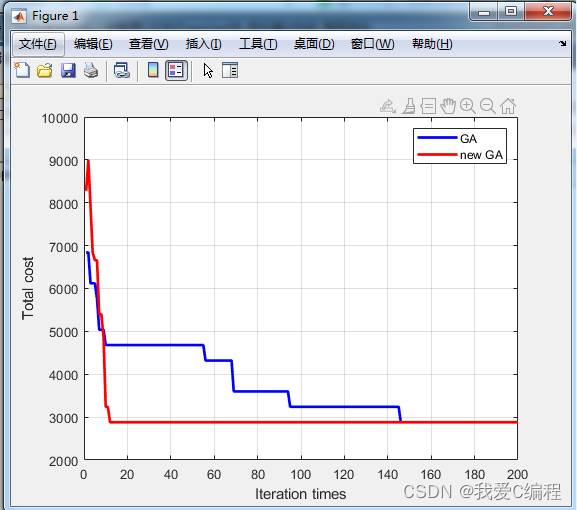
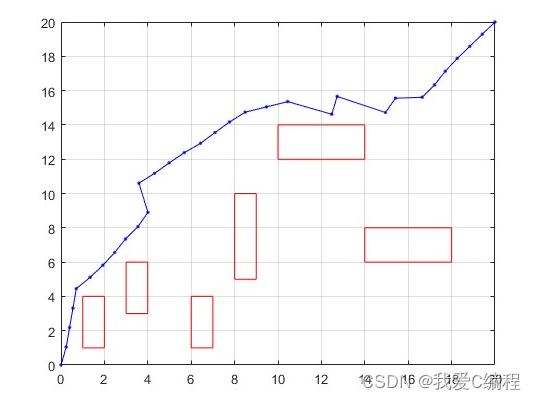
2.仿真效果预览

matlab2022a仿真如下：

 

3.MATLAB核心程序

%编号
NO    = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]';
%线路首端号
START = [1,1,1,1,1,2,2,2,2,3,3,3,4,4,5]';
%线路末端号
ENDS  = [2,3,4,5,6,3,4,5,6,4,5,6,5,6,6]';
%支路电抗
ZDK   = [40,50,60,20,10,20,20,40,20,20,30,48,30,20,10]';
%容量限制
Vmax  = [100,100,80,100,70,100,100,100,100,82,100,100,75,100,78]';
%线路长度
Len   = [40,38,60,20,68,20,40,31,30,59,20,48,63,30,61]';
%电抗
DZ    = [0.1,0.09,0.15,0.05,0.17,0.05,0.1,0.08,0.08,0.15,0.05,0.12,0.16,0.08,0.15]';
%电抗
DK    = [0.4,0.38,0.6,0.2,0.68,0.2,0.4,0.31,0.3,0.59,0.2,0.48,0.63,0.3,0.61]';

tmps  =[NO,START,ENDS,ZDK,Vmax,Len,DZ,DK]; 
%整理
IEEE6 =[tmps([1,3,4,6,7,11],:);tmps([9,11,14],:)]; 

%初始线路
Nline =[1,1,1,1,1,1,0,0,0];   


%初始邻接矩阵
Connect=[0 1 0 1 1 0;
         1 0 1 1 0 0;
         0 1 0 0 1 0;
         1 1 0 0 0 0;
         1 0 1 0 0 0;
         0 0 0 0 0 0];
%各节点注入功率
P = [-30,-240,125,-160,-240]';             
%节点数 
N = 6;     

tic;
%定义遗传算法参数
%种群规模
NIND   = 1000;                                                                
%迭代次数
MAXGEN = 200;                                                                                                             
Price  = zeros(MAXGEN,1);          
%基向量 
BaseV  = 5*ones(1,length(Nline));
Chrom  = crtbp(20,BaseV); 
gen    = 0;   
%初始种群函数值
ObjV   = func_obj(Chrom,IEEE6,Nline,Connect,P,N); 
df     = 1000;
while gen< MAXGEN
      gen
      if gen == 0
         Pe = 0.92; 
      else
         Pe = 1/(1+exp(-df/10));  
      end
      gen   = gen+1;
      FitnV = ranking(ObjV);           
      %选择
      SelCh = select('sus',Chrom,FitnV);                              
      SelCh = recombin('xovmp',SelCh,Pe);  
      %重组
      f     = [zeros(1,length(Nline));5*ones(1,length(Nline))];      
      %变异
      SelCh        = mutbga(SelCh,f);                                               
      SelCh        = fix(SelCh);   
      ObjV2        = func_obj(SelCh,IEEE6,Nline,Connect,P,N);                                      
      [Chrom,ObjV] = reins(Chrom,SelCh,1,1,ObjV,ObjV2); 
      indx         = find(isnan(ObjV) == 1);
      ObjV3        = ObjV;
      ObjV3(indx)  = [];
      Price(gen)   = min(ObjV3);  
      if gen > 1
         df        = abs(Price(gen) - Price(gen-1));
      end
end

[Y,I]   = min(ObjV);                        
%规划
Net_new = Chrom(I,:);
Net_new
Y   
figure;
plot(Price,'b','linewidth',2);
grid on    
xlabel('Iteration times');
ylabel('Total cost');
toc; 
save R2.mat Price
02_048m

4.完整MATLAB

V