目录
1、运算电路基本认识
2、反向比例、同相比例运算电路
3、电压跟随器(同相比例的特例)
4、差分比例运算电路(减法运算电路)
5、积分、微分运算电路
1、运算电路基本认识
(集成运放工作在线性区)
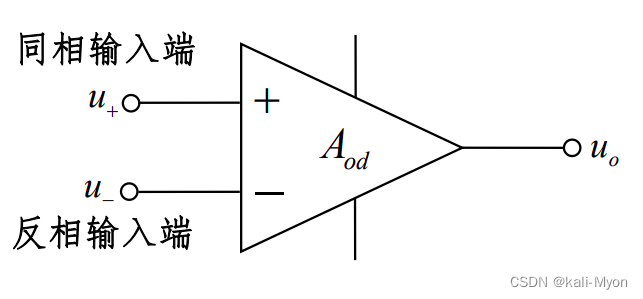
两个输入端:同相输入端u+、反相输入端u-
一个输出端:uo
开环差模放大倍数: Aod
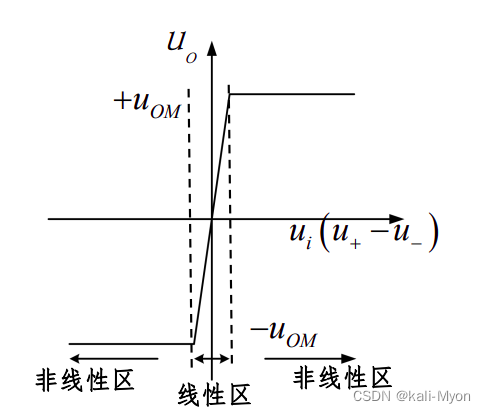
运放工作的两个区域:
(1)线性区:uo = Aod (u+-u- ) ,输出电压随输入电压线性变化
(2)非线性区:输出只有两种可能,+uOM、-uOM

工作在线性区的有:集成运算电路,滤波电路
工作在非线性区的有:电压比较器

2、反向比例、同相比例运算电路
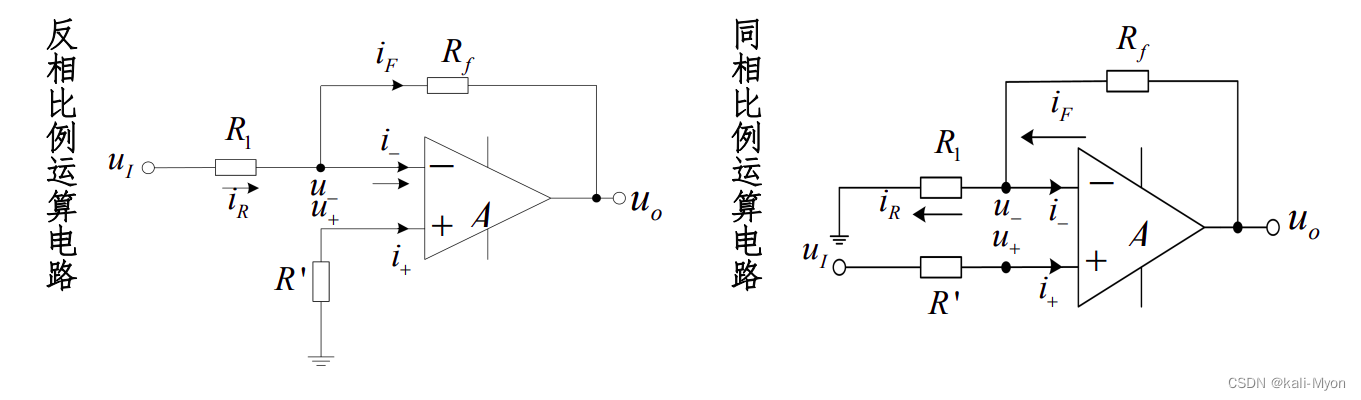
我们这里先讲的是运放的线性应用,所以是线性工作区,引入负反馈
从上面两个图我们可以看出,反馈都是接在了反向端(即接的 - )
如何区分是反向比例还是同相比例:
看输入端,从-输入,则为反向比例运算电路;从+输入,即为同相比例运算电路。
并且一端接输入电压,另一端则接地。
反向比例、同相比例中uo与ui的关系:
对于反向比例,有:
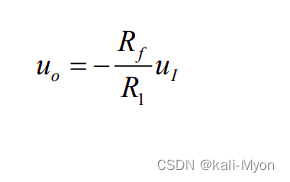
对于同相比例,有:
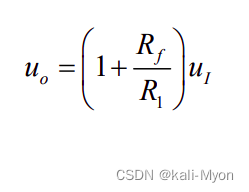
3、电压跟随器(同相比例的特例)

三种情况都可以使uo=ui,即输出电压等于输入电压。
电压跟随器具有输入阻抗高、输出阻抗低的特点,可以起到阻抗匹配的作用, 能够使得后一级的放大电路更好的工作;另外一个作用就是隔离,把电路置于前级和功放之间,可以切断后一级的反电 动势对前级的干扰作用。
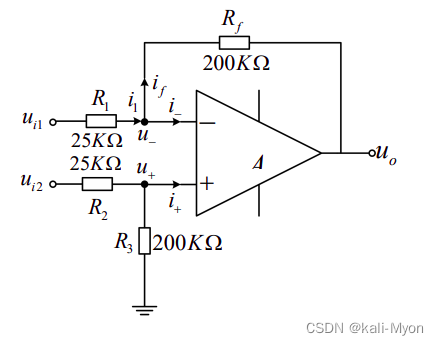
4、差分比例运算电路(减法运算电路)
当ui1和ui2都有输入时,就构成了差分比例运算电路,处理这类电路我们使用叠加定理:
使两个输入端分别单独作用,另一端接地,最后将作用效果叠加。
eg:求输出电压与输入电压的运算关系式

5、积分、微分运算电路
电容上的电压、电流:
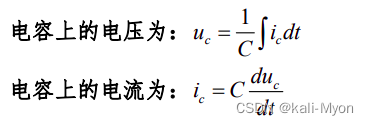
如何判断是积分电路还是微分电路?
理论上来说我们是可以通过计算出输出电压和输入电压的关系来判断
这里我们使用简单方法:看电容的位置
如图:
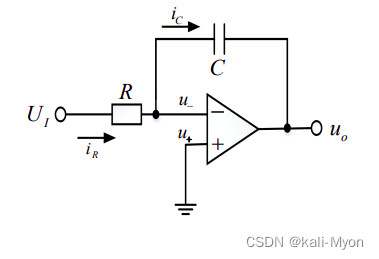
反馈上接了个电容,这就是积分电路。
对于积分电路,它可以将方波变为三角波,将正弦信号变为余弦信号(移相)。
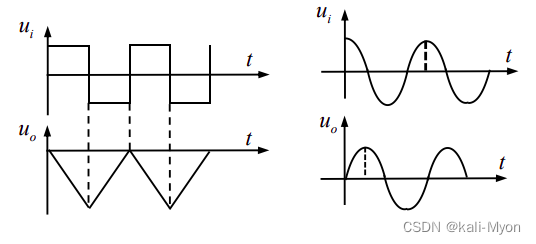
积分电路中:
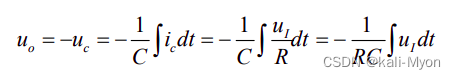
再看另一个:
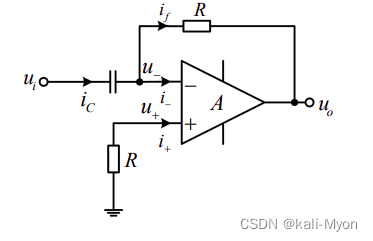
输入端ui上接了个电容,这就是微分电路。
微分电路中:
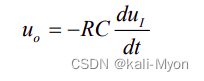

![QtXlsxWriter make报错:[Makefile:45:sub-xlsx-make_first] 错误](https://img-blog.csdnimg.cn/a9b417c058e34fcfb318e743ced3678a.png)