---

最长公共子序列

力扣连接：1143. 最长公共子序列（中等）

动态规划方法

2. 确定递推公式
   主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同（if），text1[i - 1] 与 text2[j - 1]不相同（else）

   • 如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以

     dp[i][j] = dp[i - 1][j - 1] + 1;
     

   • 如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。
     即：

     dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
     

图解步骤

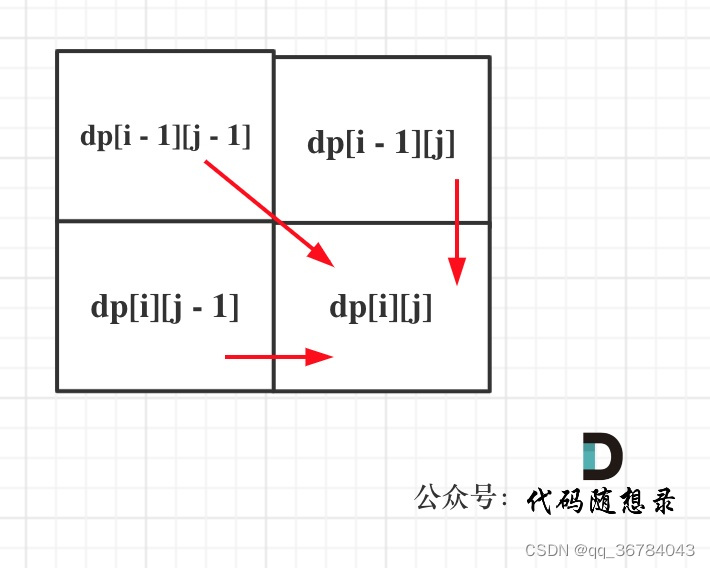
代码

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int len1 = text1.length();
        int len2 = text2.length();
        int[][] dp = new int[len1+1][len2+1];
        int max = 0;

        for(int i=1;i<=len1;i++){
            for(int j=1;j<=len2;j++){
                if(text1.charAt(i-1)==text2.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1]+1;
                }else{
                    dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
                }

                max = Math.max(max, dp[i][j]);
            }
        }

        return max;

    }
}

---

---

不相交的线

力扣连接：1035. 不相交的线（中等）

动态规划方法

和上一题一模一样。

---

---

最大子数组和

力扣连接：53. 最大子数组和（中等）

动态规划的解法，除此之外还有贪心的解法。

图解步骤

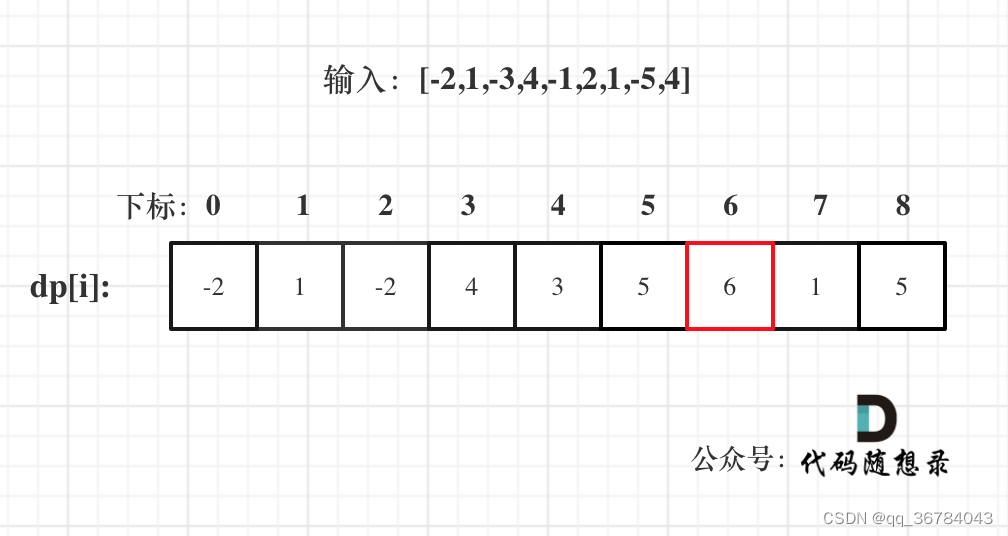
关键点：
关于dp[i]的赋值

• dp[i-1] 大于 0 时，dp[i-1] 与 nums[i] 相加。
• dp[i-1] 小于 0 时，不管它，直接赋值当前 nums[i]。

代码

class Solution {
    public int maxSubArray(int[] nums) {
        int len = nums.length;
        int[] dp = new int[len];
        dp[0] = nums[0];
        int max = dp[0];
        
        for(int i=1;i<len;i++){
            if(dp[i-1]>=0){
                dp[i] = dp[i-1] + nums[i];
            }else{
                dp[i] = nums[i];
            }

            max = Math.max(max, dp[i]);
        }

        return max;
    }
}

---

---