简介
一个质点从t=0出发,随着时间有不同的构形,运动的描述是运动学。
所以需要建立运动方程来表征连续体是如何演化及其性质(例如位移、速度、加速度、质量密度、温度等)如何随时间变化
初始构形 或者 参考构形: B 0 \mathcal{B}_0 B0
当前构形: B t \mathcal{B}_t Bt
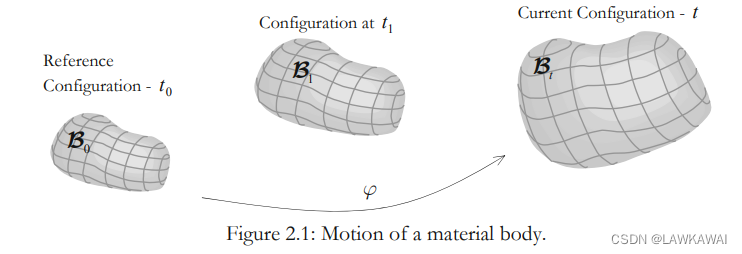
从描述单个质点的运动开始
研究在变形当中质点之间的相对距离
定义变形和应变张量,在这之前先定义连续性质
连续介质
任何介质都有质量
如果连续体在任何地方性质一致,被称为齐次的
考虑某个点P为中心的球作为初始构形:
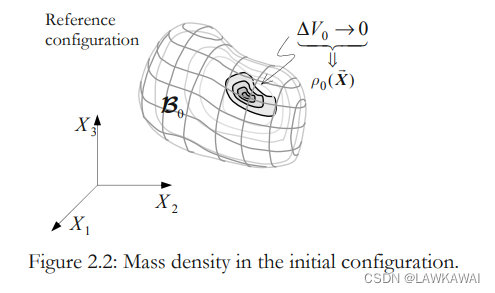
体积:
Δ
V
0
\Delta V_0
ΔV0
质量:
Δ
m
\Delta m
Δm
那么,质量密度:
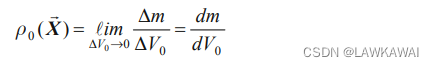
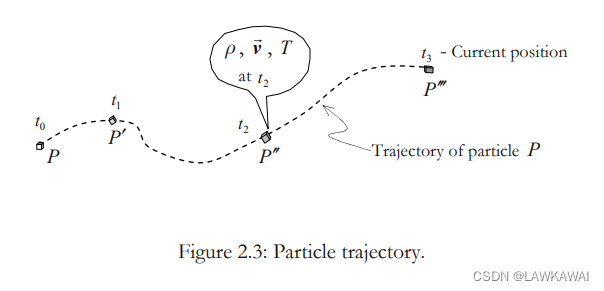
质点: 一个微小体积元,所具有的确定的性质,例如 质量密度、速度、温度等
点: 空间中的一个点
质点迹线: 单个质点运动过程中的轨迹
运动的类型
刚体运动:保持原来的构形,表征为质点之间的距离保持一致;可以分类为:位移和旋转
带变形的运动:表征为质点之间的距离会发生变化
刚体运动
建立运动方程,直角坐标系 O X 1 X 2 X 3 OX_1X_2X_3 OX1X2X3 在刚体上,所以任意质点的位置向量在运动过程中是不会发生改变的
另一个直角坐标系 o x 1 x 2 x 3 ox_1x_2x_3 ox1x2x3 表示正交基 ( e ^ 1 , e ^ 2 , e ^ 3 ) (\hat e_1, \hat e_2, \hat e_3) (e^1,e^2,e^3)
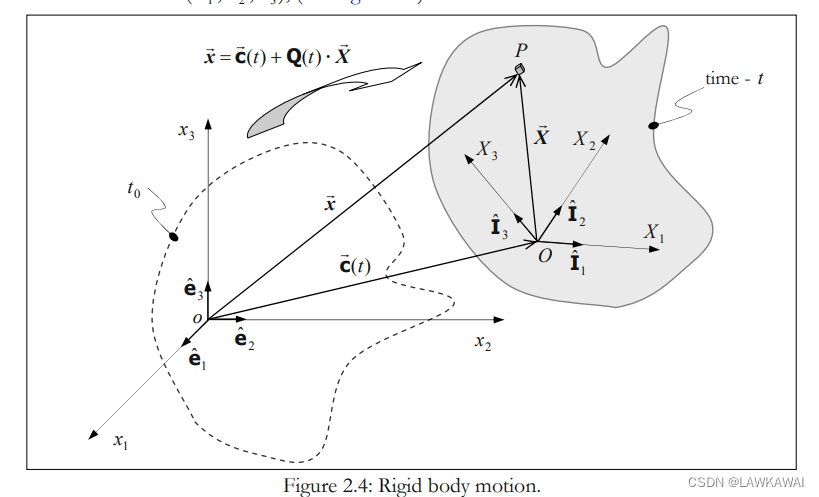
质点P在坐标系
e
^
i
\hat e_i
e^i 和
I
^
i
\hat I_i
I^i 的位置向量为
X
⃗
\vec X
X 和
x
⃗
\vec x
x
那么:
x
⃗
=
c
⃗
+
X
⃗
\vec x = \vec c + \vec X
x=c+X
其中
c
⃗
(
t
)
\vec c(t)
c(t) 与时间相关,描述的是坐标系
I
^
i
\hat I_i
I^i 的位移运动
下标表示:
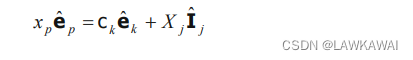
在
o
x
1
x
2
x
3
ox_1x_2x_3
ox1x2x3的分量 可以点乘
e
^
i
\hat e_i
e^i 得到:
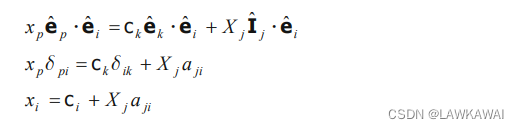
其中
I
^
j
⋅
e
^
i
=
a
j
i
\hat I_j \cdot \hat e_i = a_{ji}
I^j⋅e^i=aji 表示从坐标系
I
^
i
\hat I_i
I^i 到坐标系
e
^
i
\hat e_i
e^i 的变换矩阵
并且 a i k a k j = δ i j a_{ik} a_{kj} = \delta_{ij} aikakj=δij , a j i a_{ji} aji 是一个正交矩阵
考虑
Q
i
j
=
a
j
i
Q_{ij} = a_{ji}
Qij=aji , 那么:
x
⃗
=
c
⃗
+
Q
⋅
X
⃗
刚体运动方程
\boxed{\vec x = \vec c + Q \cdot \vec X} 刚体运动方程
x=c+Q⋅X刚体运动方程
NOTE: 分量的变换定律和正交变换密切相关,但它们有着完全不同的含义
问题2.1 一个连续体是以b为边的正方形,受到一个刚体运动,这个刚体运动是以逆时针旋转30°的旋转运动,求出运动方程,并求出质点D的新的位置

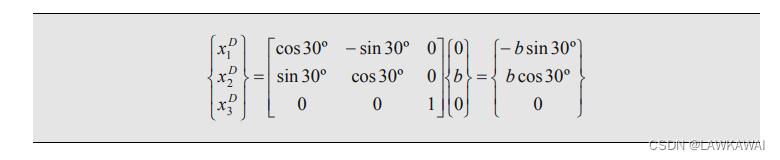
c
⃗
=
0
⃗
\vec c = \vec 0
c=0, 所以空间坐标系和质点坐标系重叠了

构形的类型
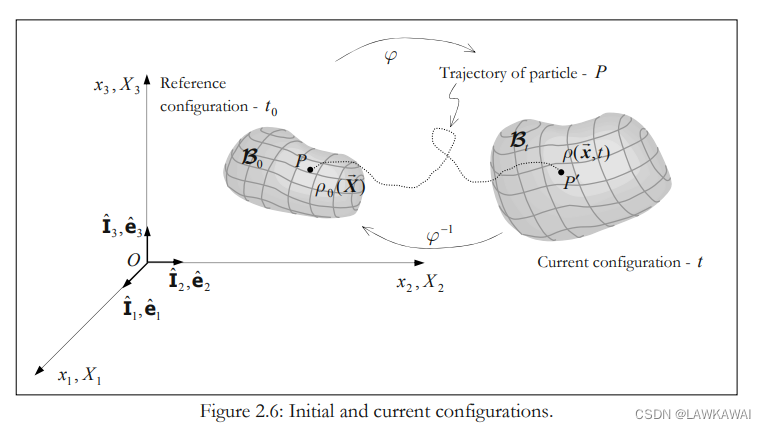
参考构形 或者 初始构形: 在时间 t ≡ t 0 t \equiv t_0 t≡t0, 即未变形之前的构形,质点P的位置向量为 X ⃗ P \vec X^P XP
当前构形 或者 变形构形: 在时间 t = t t = t t=t 的构形
运动可以表征为一个双射函数 φ \varphi φ ,这可以保证存在逆函数 φ − 1 \varphi ^{-1} φ−1
质量密度
当前构形的质量密度:
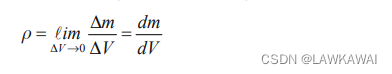
质量密度是一个标量场,是一个关于位置和时间的函数:
ρ
=
ρ
(
x
⃗
,
t
)
\rho=\rho(\vec x, t)
ρ=ρ(x,t)
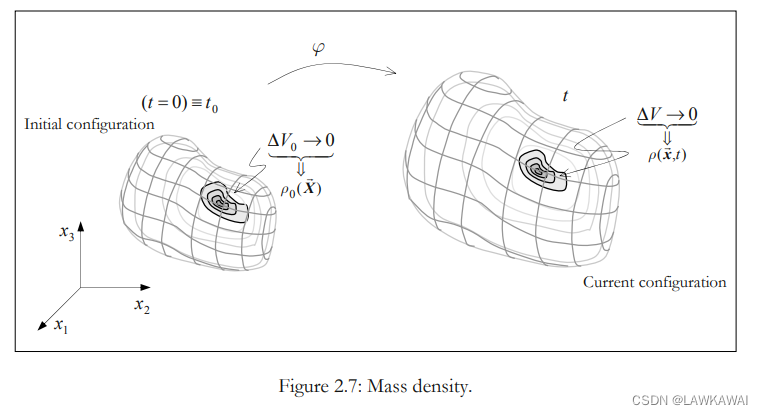
运动的描述
质点和空间坐标系
质量体 B 0 \mathcal B_0 B0 在初始构形
在任意时间,质量体会占据一个新的空间 B t \mathcal B_t Bt ,考察质点P
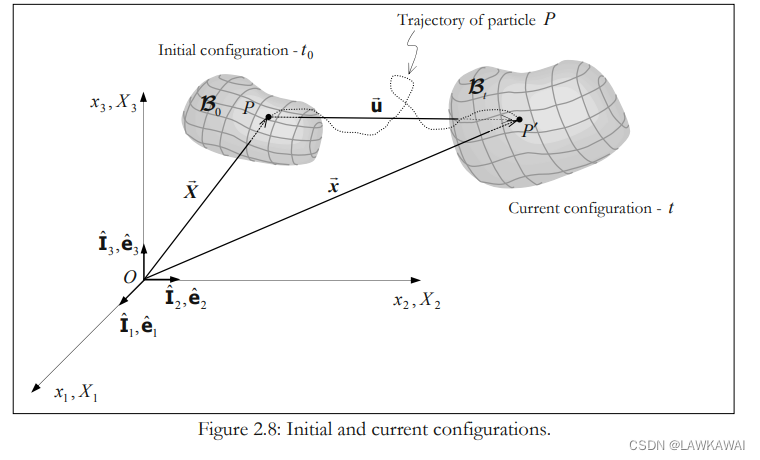
质点P在参考构形,时间t=0的位置向量为:
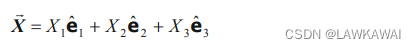
定义质点坐标系:

质点P在当前构形位于位置 P’, 位置向量为:

其中,定义了空间坐标系:

位移向量
位移向量定义为当前构形的位置向量
x
⃗
\vec x
x 和参考构形的位置向量
X
⃗
\vec X
X的差:
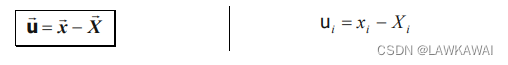
速度向量
定义为位置向量的变化率:
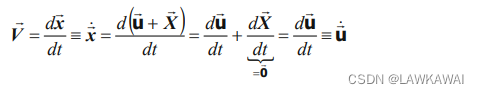
加速度向量
定义为速度向量的变化率:
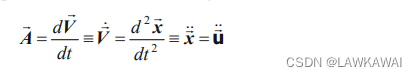
拉格朗日描述和欧拉描述
连续的性质:质量密度、温度、速度、加速度是质点固有的,这些性质可以随着时间变化,连续运动可以表征为一个双射的函数 φ \varphi φ 和逆函数 φ − 1 \varphi^{-1} φ−1
这保证了我们可以联系当前构形和参考构形之间的连续性质
运动的拉格朗日描述
用质点坐标系
X
⃗
\vec X
X 表示的质点运动:
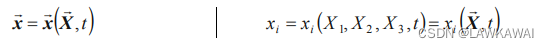
这个运动方程被称为拉格朗日运动描述
这个方程给出了在当前时刻 t 的位置 x ⃗ \vec x x, 其中质点在时刻 t = t 0 t = t_0 t=t0 占据着位置 X ⃗ \vec X X
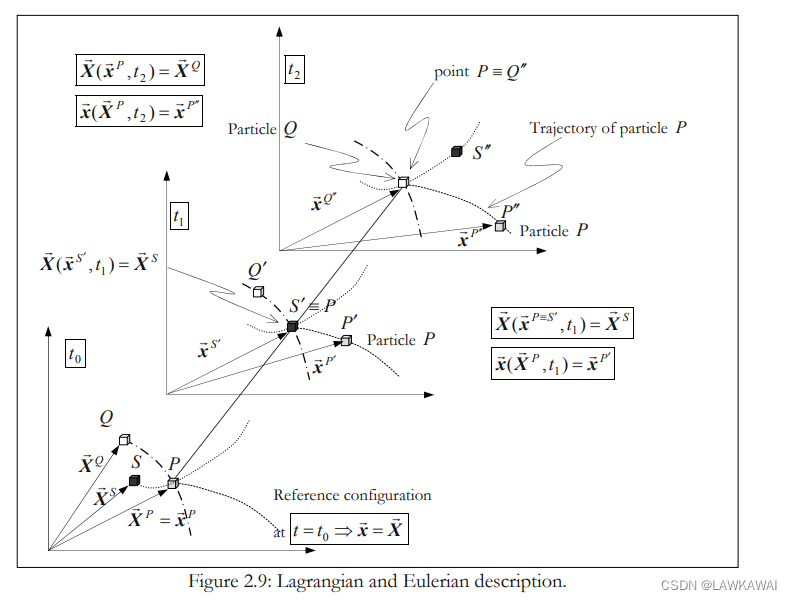
上面的方程如果应用于某个质点P, 则该方程描述的是这个质点的迹线
运动的欧拉描述
用空间坐标系
x
⃗
\vec x
x表示的质点运动:
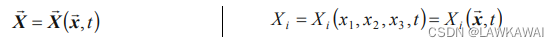
这个方程给出了在初始时刻
t
0
t_0
t0 的初始位置
X
⃗
\vec X
X, 该质点在当前时刻
t
t
t 具有坐标
(
x
1
,
x
2
,
x
3
)
(x_1, x_2, x_3)
(x1,x2,x3)
在
t
=
0
t=0
t=0时刻有:
x
⃗
P
(
X
⃗
,
t
=
0
)
=
X
⃗
P
\vec x^P(\vec X, t=0)=\vec X^P
xP(X,t=0)=XP
质点P的迹线:
x
⃗
(
X
⃗
P
,
t
0
)
=
X
⃗
P
→
x
⃗
(
X
⃗
P
,
t
1
)
=
X
⃗
P
′
→
x
⃗
(
X
⃗
P
,
t
2
)
=
X
⃗
P
′
′
\vec x(\vec X^P,t_0)=\vec X^P \rightarrow \vec x(\vec X^P,t_1)=\vec X^{P'} \rightarrow \vec x(\vec X^P,t_2)=\vec X^{P''}
x(XP,t0)=XP→x(XP,t1)=XP′→x(XP,t2)=XP′′
不同时刻在点P的质点:
X
⃗
(
x
⃗
P
,
t
0
)
=
X
⃗
P
→
X
⃗
(
x
⃗
S
′
,
t
1
)
=
X
⃗
S
→
X
⃗
(
x
⃗
Q
′
′
,
t
2
)
=
X
⃗
Q
\vec X(\vec x^P,t_0)=\vec X^P \rightarrow \vec X(\vec x^{S'},t_1)=\vec X^{S} \rightarrow \vec X(\vec x^{Q''},t_2)=\vec X^Q
X(xP,t0)=XP→X(xS′,t1)=XS→X(xQ′′,t2)=XQ
其中 X ⃗ ( x ⃗ S ′ , t 1 ) = X ⃗ S \vec X(\vec x^{S'},t_1)=\vec X^{S} X(xS′,t1)=XS 表示 在时刻 t 1 t_1 t1 位于点 P = S ‘ P=S‘ P=S‘的质点为S,其初始位置为 X ⃗ S \vec X^S XS
存在逆的充分必要条件是:雅可比行列式不为0

**不可穿透性公理:**两个粒子不能同时占据同一位置。如后所述,当雅可比行列式为正时,这个条件是确定的
拉格朗日变量和欧拉变量
在连续体 B \mathcal B B 上的物理量 Z \mathcal Z Z 可以表达成:
拉格朗日形式 : ( Z ( X ⃗ , t ) ) (Z(\vec X, t)) (Z(X,t))
欧拉形式: z ( x ⃗ , t ) z(\vec x, t) z(x,t)
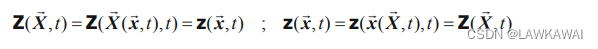
问题2.2 考虑以下拉格朗日描述的运动方程:


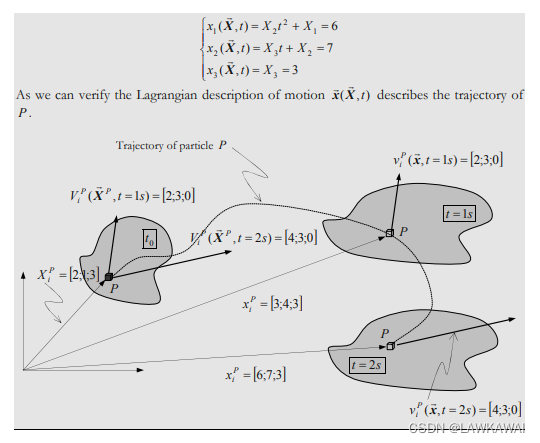
质点时间导数
随时间变化的导数: D D t \frac{D}{Dt} DtD
跟着质点P运动并且记录随着时间变化的温度

如果属性是由拉格朗日描述:
θ
=
θ
(
X
1
,
X
2
,
X
3
,
t
)
\theta = \theta(X_1, X_2, X_3, t)
θ=θ(X1,X2,X3,t)
这种情况下,质点的时间导数表示为:
θ ˙ ( X ⃗ , t ) ≡ D θ ( X ⃗ , t ) D t = d θ ( X ⃗ , t ) d t \boxed{\dot \theta (\vec X, t)\equiv\frac{D\theta(\vec X, t)}{Dt}=\frac{d\theta (\vec X, t)}{dt}} θ˙(X,t)≡DtDθ(X,t)=dtdθ(X,t)
这个属性是由质点坐标系描述的,意味着该属性与同一个质点运动过程相连接
如果属性是由欧拉描述:
θ
=
θ
(
x
1
,
x
2
,
x
3
,
t
)
\theta = \theta(x_1, x_2, x_3, t)
θ=θ(x1,x2,x3,t)
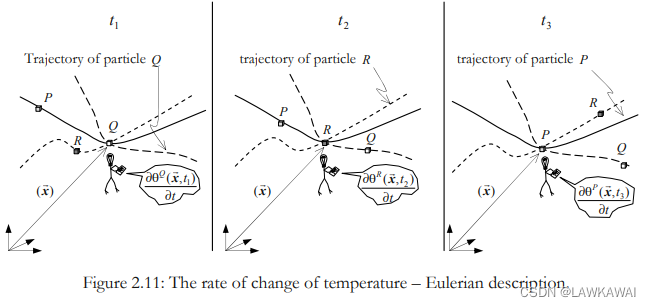
观察不再跟踪质点P,而是固定在某个点
(
x
1
,
x
2
,
x
3
)
(x_1, x_2, x_3)
(x1,x2,x3),观察经过的质点
在时刻
t
1
t_1
t1: 观测到质点Q的属性
在时刻
t
2
t_2
t2: 观测到质点R的属性
在时刻
t
3
t_3
t3: 观测到质点P的属性
需要强调的是质点的时间导数与质点的固有属性关于时间的导数有关,例如,这是关于同一个质点的
然而,一个固定在某个点的观察者,只能得到当地的变化率的信息
为了得到完整的信息,我们需要知道质点沿着迹线其属性是怎么变化的,而这个额外的信息被称为对流的变化率,这与质量输运有关
所以,为了得到质点的时间导数,必须考虑以下两项:
- 当地变化率
- 对流变化率
所以:

质点速度: v ⃗ ( X ⃗ , t ) = x ⃗ ˙ ( X ⃗ , t ) \vec v(\vec X, t)=\dot {\vec x}(\vec X, t) v(X,t)=x˙(X,t)
欧拉描述: v ⃗ ( X ⃗ ( x ⃗ , t ) , t ) = v ⃗ ( x ⃗ , t ) \vec v(\vec X(\vec x, t), t)=\vec v(\vec x, t) v(X(x,t),t)=v(x,t)
可以定义欧拉描述下的时间导数算子:
∗
(
x
⃗
,
t
)
*(\vec x, t)
∗(x,t)
D
∗
(
x
⃗
,
t
)
D
t
=
∂
∗
(
x
⃗
,
t
)
∂
t
+
∇
x
⃗
∗
(
x
⃗
,
t
)
⋅
v
⃗
(
x
⃗
,
t
)
欧拉描述的质点时间导数
\boxed{\frac{D * (\vec x, t)}{Dt}=\frac{\partial *(\vec x, t)}{\partial t}+\nabla_{\vec x}*(\vec x, t)\cdot \vec v(\vec x, t)}欧拉描述的质点时间导数
DtD∗(x,t)=∂t∂∗(x,t)+∇x∗(x,t)⋅v(x,t)欧拉描述的质点时间导数
下标形式:
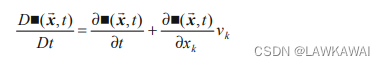
欧拉描述的速度和加速度
质点P的速度:
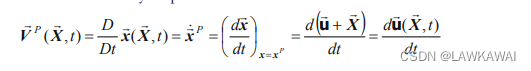
这是拉格朗日描述
为了得到欧拉描述,需要代入运动逆方程:
V
⃗
P
(
X
⃗
,
t
)
=
V
⃗
P
(
X
⃗
(
x
⃗
,
t
)
,
t
)
=
v
⃗
P
(
x
⃗
,
t
)
\vec V^P(\vec X, t)=\vec V^P(\vec X (\vec x, t), t)=\vec v^P(\vec x, t)
VP(X,t)=VP(X(x,t),t)=vP(x,t)
质点的加速度:
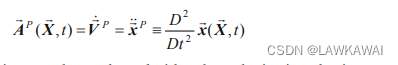
欧拉描述可以用逆方程代入得到或者通过应用欧拉描述的质点时间导数的定义:
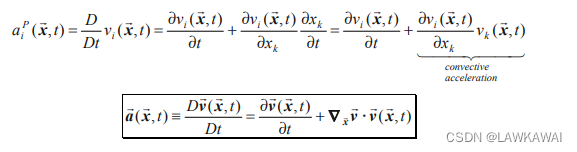
欧拉加速度的矩阵形式:
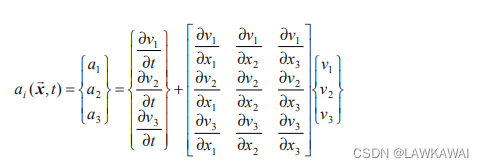
回到问题2.2
欧拉速度场:
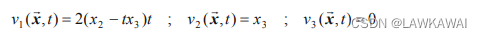
那么,欧拉加速度也可以用定义得到:
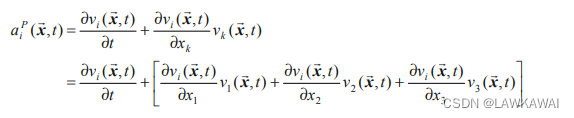
加速的各个分量如下:
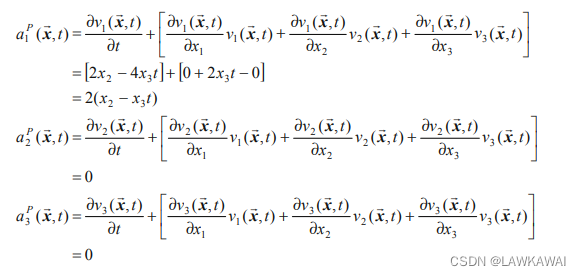
与问题2.2得到的结果一样
定常场
一个场
ϕ
(
x
⃗
,
t
)
\phi(\vec x, t)
ϕ(x,t) 是定常的,如果其当地变化率不随时间发生变化:
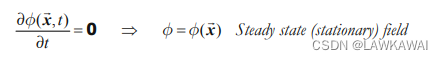
定常的速度场: 在时刻
t
1
t_1
t1 和时刻
t
2
t_2
t2 不发生改变

然而,这不意味着质点的速度在场当中不随时间变化
在固定的空间点
x
⃗
∗
\vec x^*
x∗:
质点Q在时刻
t
1
t_1
t1 以速度
v
⃗
∗
\vec v^*
v∗通过点Q, 此时另一个质点P的速度为
v
⃗
P
(
t
1
)
≠
v
⃗
∗
\vec v^P(t_1)\neq \vec v^*
vP(t1)=v∗
质点P在时刻
t
2
t_2
t2 通过点
x
⃗
∗
\vec x^*
x∗, 由于是定常场,所以
v
⃗
P
(
t
2
)
=
v
⃗
∗
\vec v^P(t_2)=\vec v^*
vP(t2)=v∗
所以,在定常场,质点的速度是可以发生改变的
那么,质点速度的时间导数为:
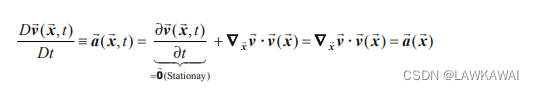
由于定常场,所以速度的变化率(加速度)为0, 如果是定常场
∂
v
⃗
(
x
⃗
,
t
)
∂
t
=
0
\frac{\partial \vec v(\vec x, t)}{\partial t}=0
∂t∂v(x,t)=0且均匀的(
∇
x
⃗
v
⃗
=
0
\nabla_{\vec x}\vec v =0
∇xv=0)
同样地,可以验证虽然空间速度与时间无关,但这不意味着物质速度也是,例如:
v
⃗
(
x
⃗
)
=
v
⃗
(
x
⃗
(
X
⃗
,
t
)
)
=
v
⃗
(
X
⃗
,
t
)
\vec v(\vec x)=\vec v(\vec x(\vec X, t))=\vec v(\vec X, t)
v(x)=v(x(X,t))=v(X,t)
流线
在时刻 t 给定一个空间速度场,可以定义流线为:每个点的切线与速度的方向相同所组成的曲线
一般情况下:流线和迹线并不重合,但在定常场下重合
问题2.3 加速度向量场定义如下

问题2.4: 考虑运动方程 x ⃗ ( X ⃗ , t ) \vec x(\vec X, t) x(X,t) 以及温度场 T ( x ⃗ , t ) T(\vec x, t) T(x,t)


参考教材:
Eduardo W.V. Chaves, Notes On Continuum Mechanics