本章重点：浮点数在内存中的存储

浮点数：数学中的小数

eg.123.45    12.345*10^1     1.2345*10^2

1E10：1.0*10^10

整型家族的类型，表示范围：limits.h

浮点数：float.h

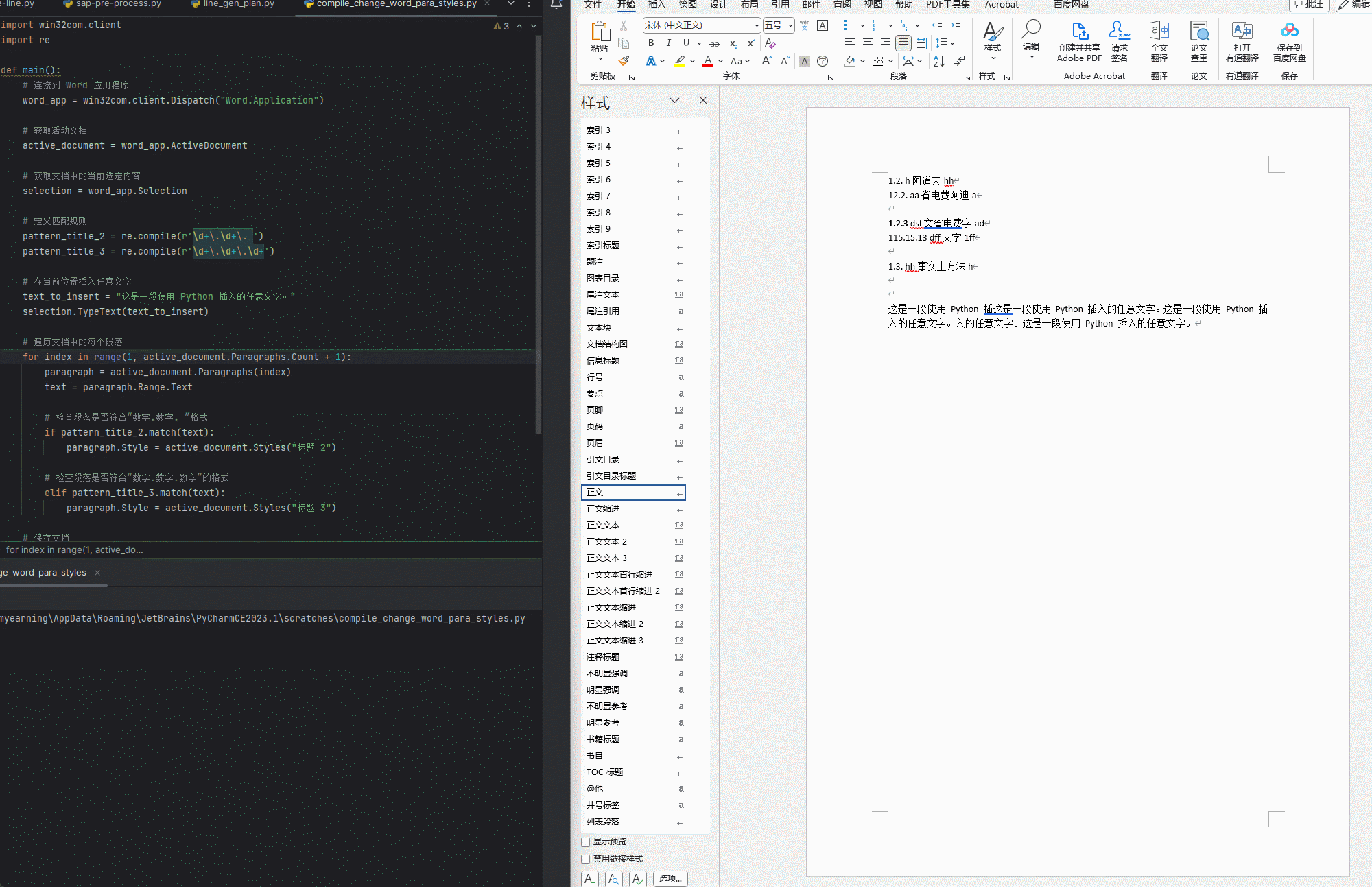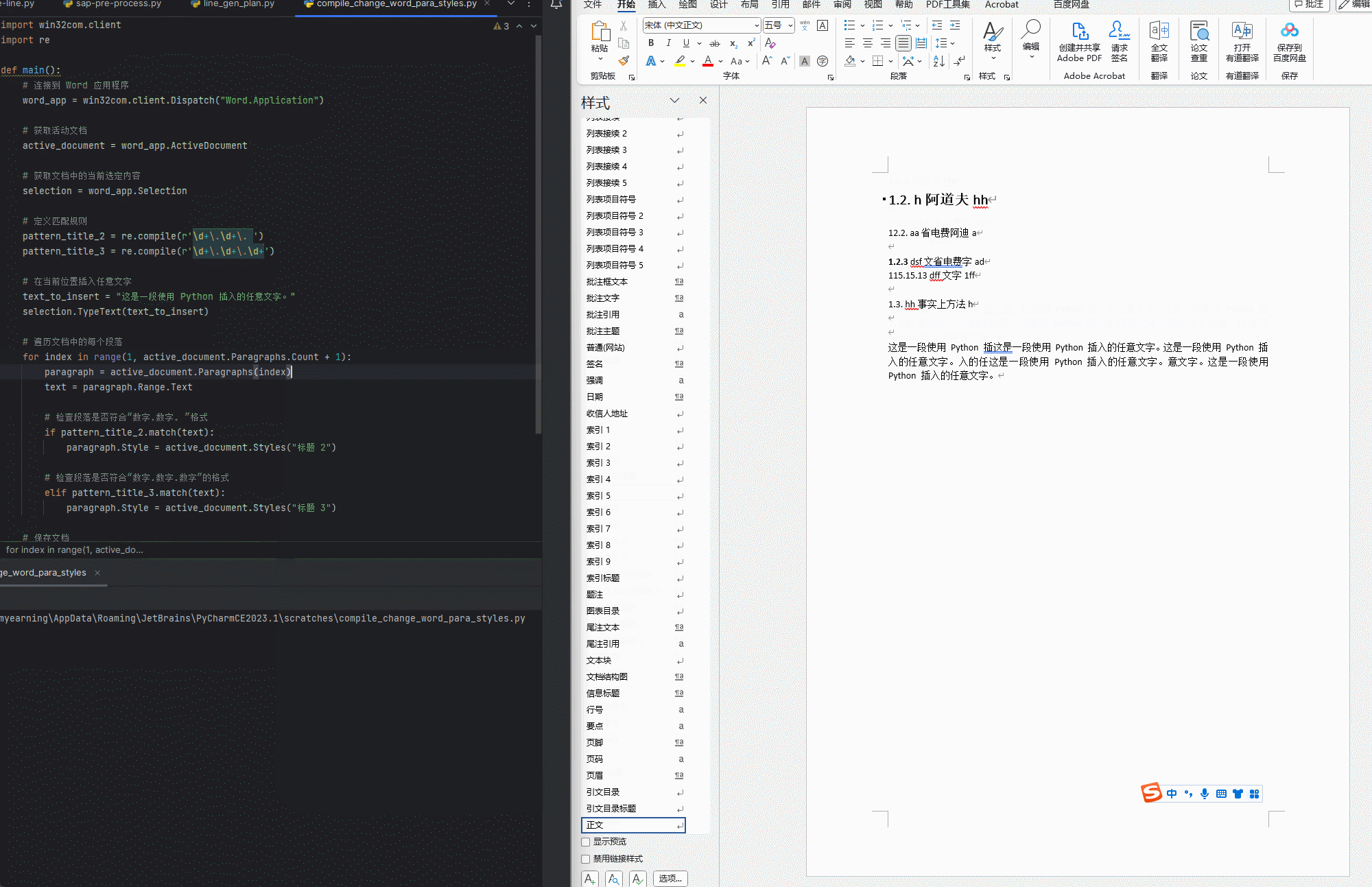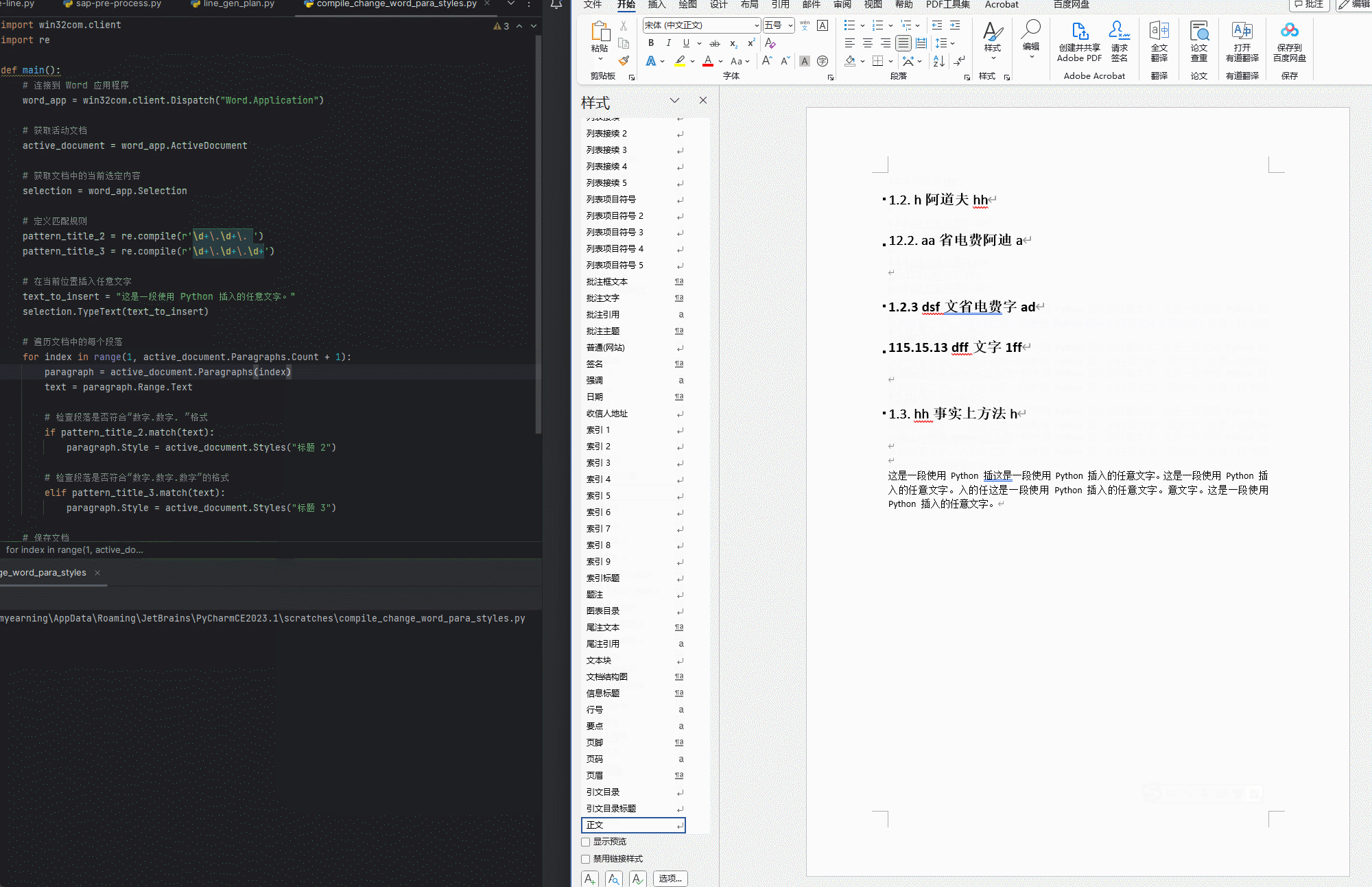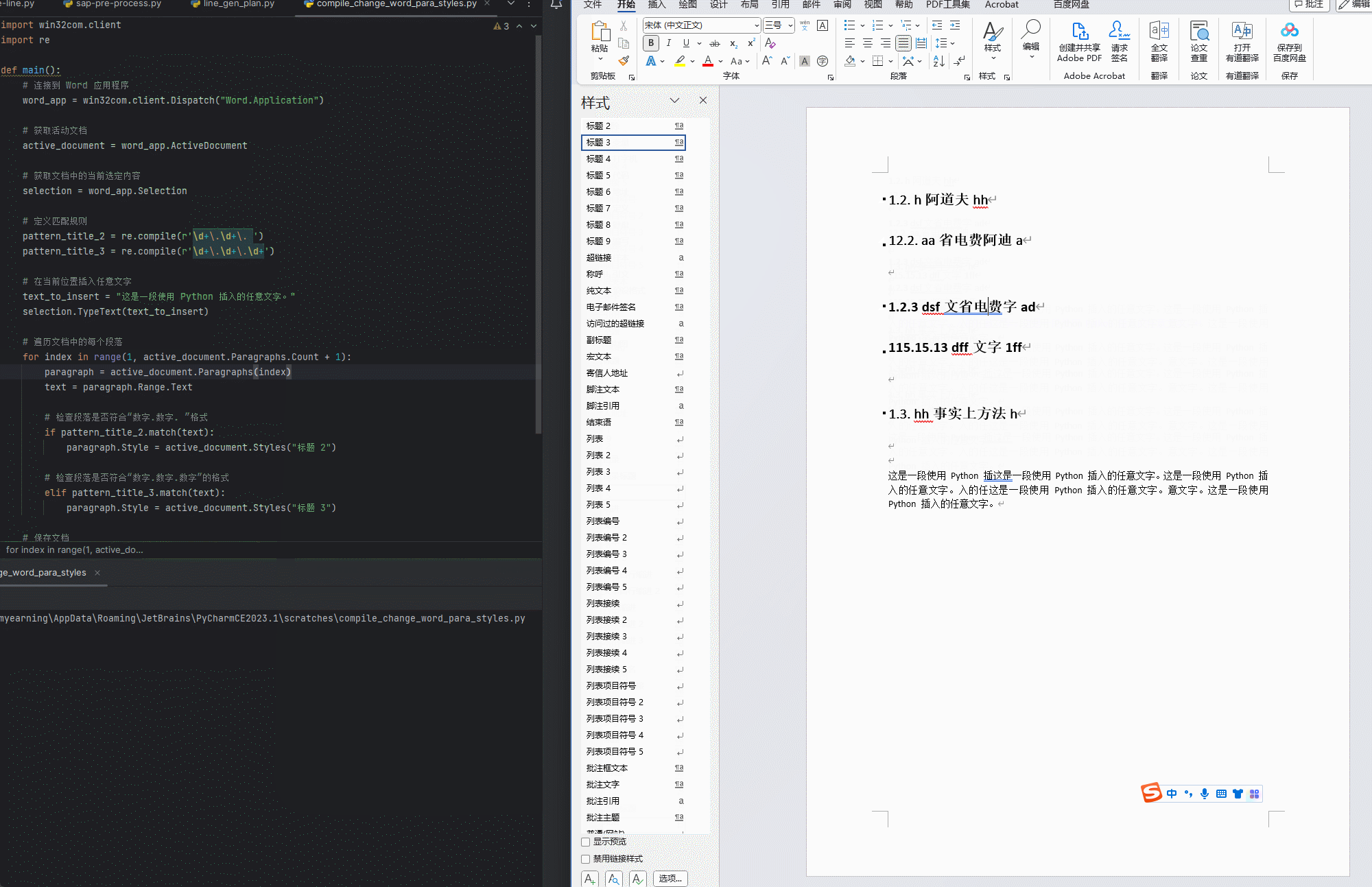
大家可以猜测一下打印的这四个数字是多少？？？

相信很多都只对了两个，大家可能会产生诱惑为什么是这个答案呢，下面给大家详细讲解

整型和浮点型在内存中的存储是有差异的

 E简单理解就是往后整数部分往后移了几位就是几，比如往后移了两位E就等于2

 给大家画个图举个例子，看下图

1.存储规则
任意一个二进制浮点数V可以表示成下面的形式：
(-1)^S * M * 2^E
(-1)^S表示符号位，当S=0，V为正数；当S=1，V为负数。
M表示有效数字，大于等于1，小于2。
2^E表示指数位。
举例来说：
十进制的10.0，写成二进制是 1010.0 ，相当于 1.01×2^3 。
那么，按照上面V的格式，可以得出S=0，M=1.01，E=3。
十进制的-10.0，写成二进制是 -1010.0 ，相当于 -1.01×2^3。那么，S=1，M=1.01，E=3。
这样应该能理解浮点数表示形式了吧！
让我们在看看这样的浮点数如何存储在内存中：
对于 32位 的浮点数，最高的1位是符号位S，接着的8位是指数E，剩下的23位为有效数字M。
对于 64位 的浮点数，最高的1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M。
对于有效数字M，还有一些特别规定：
前面说过， 1≤M<2 ，也就是说，M可以写成 1.xxxxxx 的形式，其中xxxxxx表示小数部分。
IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的，见下图

尝试着自己理解一下E不全为0或E不全为1的概念，我们讲解一下E为全0的概念       

见下图我们可以发现，这是一个非常非常小的数字，所以我们规定（见上图），当然，这种特殊情况我们以后遇见了再给大家详细讲解

特殊情况E为全1或E为全0我们先暂时不管，等到遇到特殊情况的时候我们再详细展开

现在我们会过头来看我们最开始写的那段代码，现在我给大家做一下解释，请大家看我代码旁的注释，希望大家能看懂，不怎么能看懂的可以在评论区提问或者私信我哈！！！

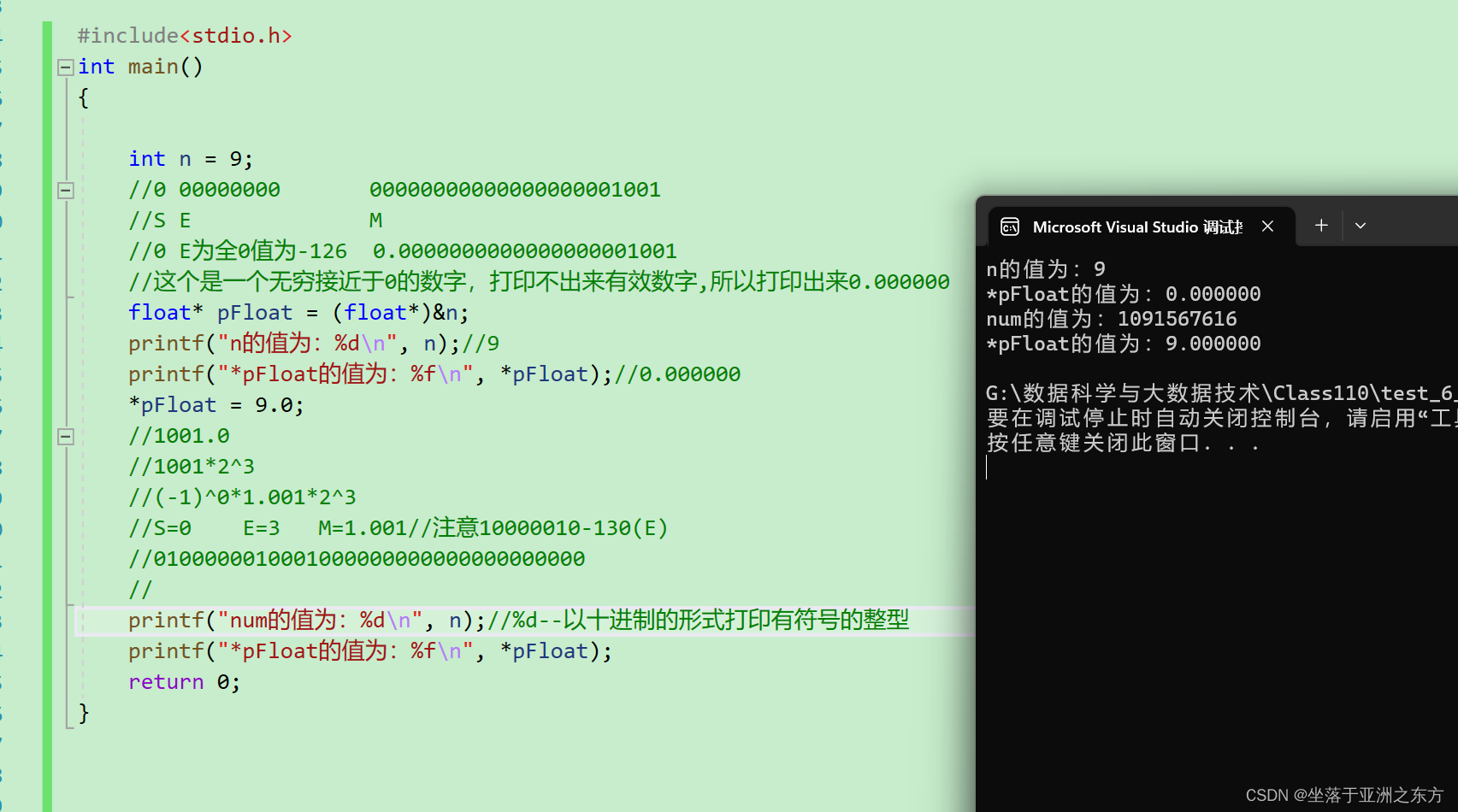
希望大家能够理解 

全章终，下一篇博客我们讲解函数初阶，大家多多支持，谢谢啦！