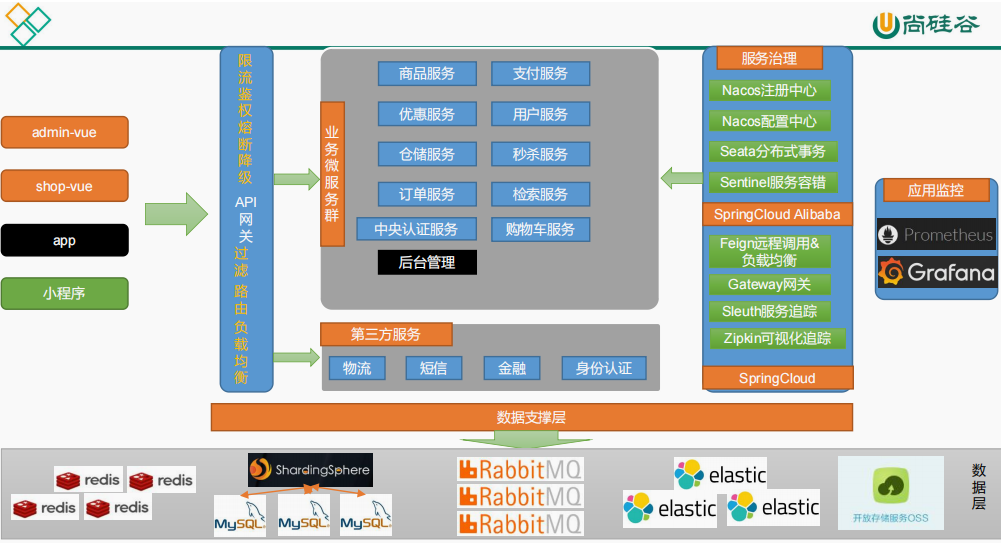
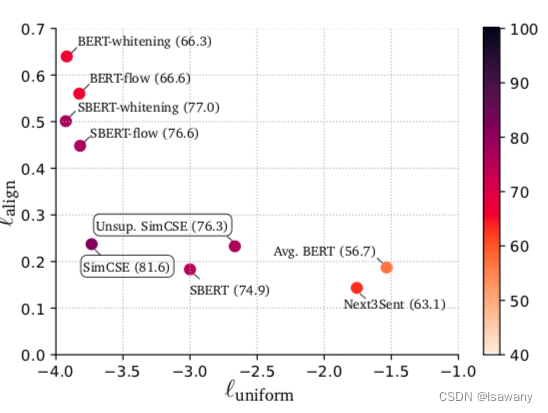
目录
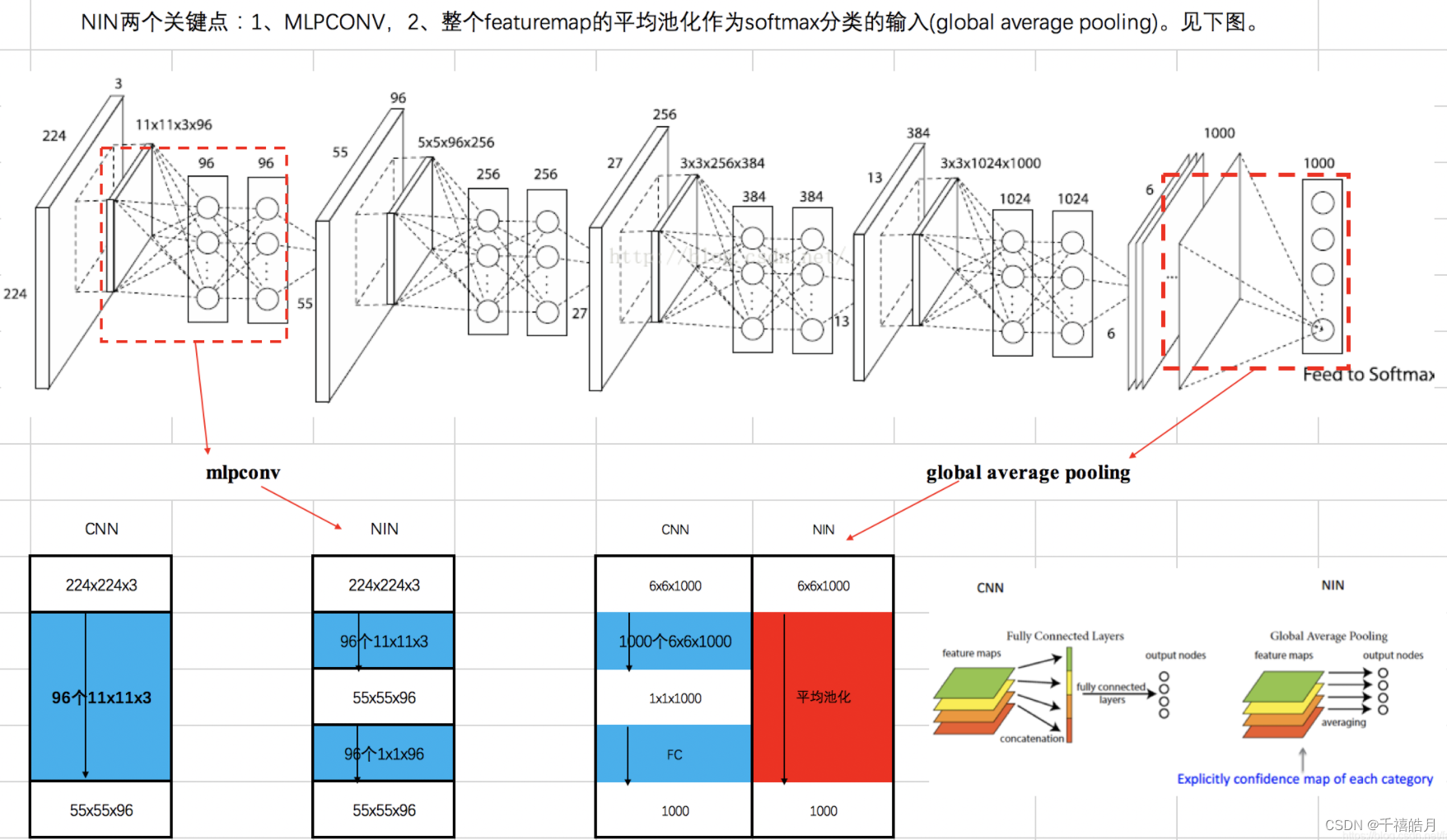
一、灰狼算法
二、改进策略
2.1 混沌初始化种群
2.2 非线性收敛因子
三、引入莱维飞行
四、运行结果
从改进运行结果来看,效果非常好,在、
、
等极易陷入局部最优的测试函数上都取到了最优值,收敛速度也得到极大提升。
一、灰狼算法
http://t.csdn.cn/nG9Xo

二、改进策略
2.1  混沌初始化种群
混沌初始化种群
初始种群位置均匀分布于搜索空间,有助于增强算法全局搜索能力,提高搜索效率。标准灰狼算法随机初始化种群,存在降低种群多样性的风险,而混沌映射生成的混沌序列,具有遍历性、非线性和不可预测性等特征,常用于替代随机序列初始化种群。本文采用映射初始化灰狼种群。作为混沌映射的典型形式,
映射具有参数简单,分布均匀等优点,其数学表达形式如下:
其中,
映射具有混沌行为。生成混沌序列
,用于初始化灰狼种群位置,如下式所示:
其中与
为搜索空间上界与下界。
2.2 非线性收敛因子
标准GWO算法通过收敛因子 a 调节参数 A ,从而平衡算法的全局搜索与局部搜索能力。复杂优化问题往往存在多个局部最优值,线性递减的更新策略决定了算法的全局搜索过程仅为全期过程的一半,算法跳出局部最优值的能力较弱。基于此,本文提出一种新的非线性收敛因子更新公式:

![]()
上述非线性收敛因子 a 的仿真如图1所示。由图1收敛曲线可以看出:与其他更新策略相比,在迭代的前期,a 取值较大且衰减速度较慢,全局搜索能力较强,促使种群在搜索空间内广泛搜索,有利于避免种群陷入局部最优值。在迭代后期,a 迅速衰减至较少的值,局部搜索能力较强,在小范围内精细搜索,有利于加速种群收敛。因此本文提出的非线性收敛因子更新策略可以更好地应用于非线性复杂优化问题的求解。

三、引入莱维飞行
标准GWO算法种群位置更新公式仅由三头精英狼主导,在搜索过程中,当精英狼陷入局部最优时,种群搜索将陷入停滞。但是算法跳出局部最优的能力较弱。布谷鸟算法中 Levy 飞行策略,可以增强算法的全局搜索能力,其特征是搜索范围远近交替地随机飞行。将 Levy 飞行引入粒子群优化(particle swarm optimization,PSO)算法,避免算法早熟收敛。引入Levy飞行策略帮助灰狼算法增大搜索范围,跳出局部最优,改进后的位置更新公式为:
其中,为采用Levy飞行策略更新后的灰狼个体位置;
为步长调节系数,将非线性调节策略应用于
的更新,
。在迭代前期,较大的
扩宽
飞行在解空间的搜索路径。在迭代后期,较小的
有利于提高算法的局部搜索能力,加速算法收敛。
为飞行步长,计算公式如下:

其中,通常取值于[0,2]之间,这里取值1.5。
四、运行结果
F5:


The best optimal value of the objective funciton found by GWO is : 26.1565
The best optimal value of the objective funciton found by LGWO is : 28.6354
The best optimal value of the objective funciton found by L1GWO is : 0
F6:


The best optimal value of the objective funciton found by GWO is : 0.24963
The best optimal value of the objective funciton found by LGWO is : 1.0624
The best optimal value of the objective funciton found by L1GWO is : 0
F8:
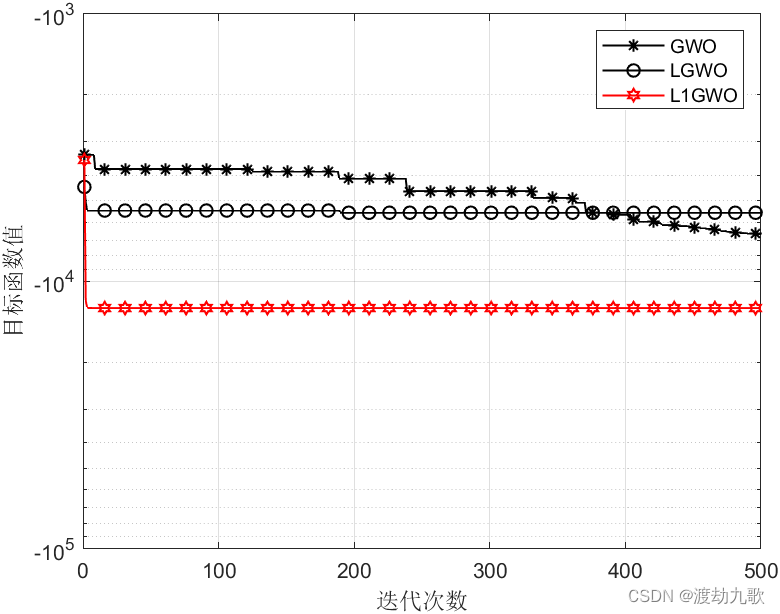
The best optimal value of the objective funciton found by GWO is : -6330.3164
The best optimal value of the objective funciton found by LGWO is : -5844.2913
The best optimal value of the objective funciton found by L1GWO is : -12569.4866