因为有个需求是判断线是否被视锥体裁切，因为NDC比较好判断是否裁切，所以研究了一下透视投影变换的函数图像。

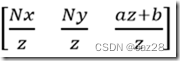
从透视投影矩阵可以看出，在同一个z上，x,y都是线性的，所以这里主要研究z的变换函数图像。
我用的是Vulkan，跟D3D的ndc一样，z是0~1的。
下面这个near=0.1,far = 2,横轴是点到相机的距离，纵轴是变换后的z坐标。

点是随机取的，从图像上看，这个函数不是线性的。
far=2这个太小了，我们看看不同的far的图像：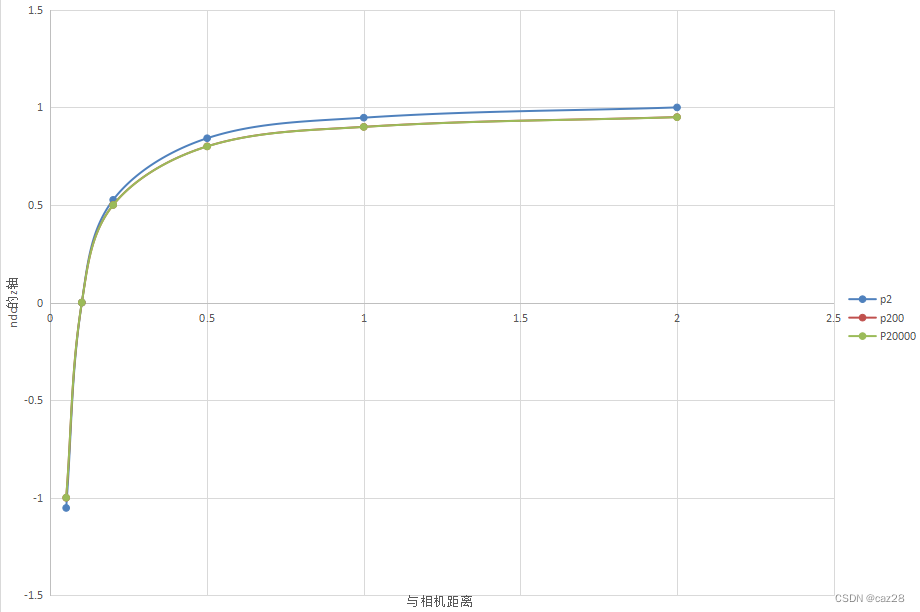

可以看到不同far差别不大，我们只显示了一部分，横轴2以后还有很长，far=20000，要到20000左右才纵轴才到1.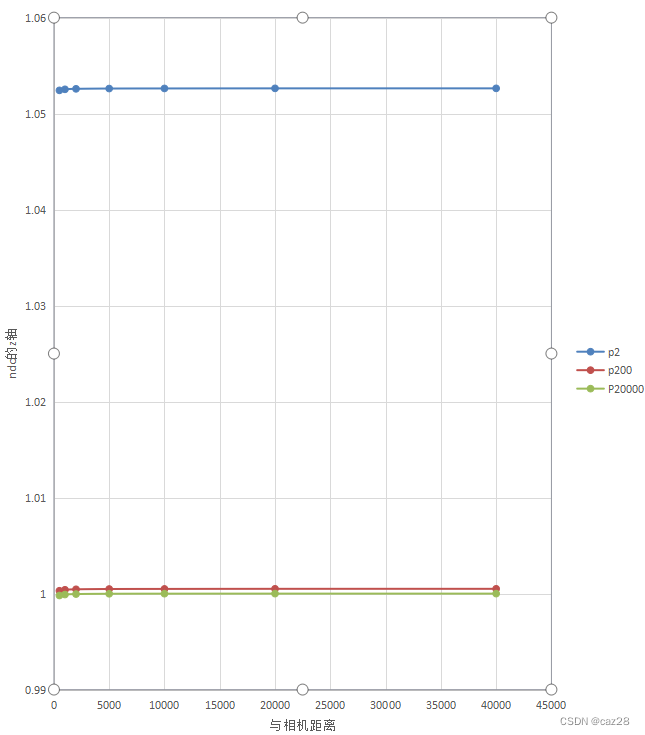

可以看到到20000左右，几乎都是水平线了。
从投影矩阵可以得到，不同near，far的曲线，在离相机无限远时，趋向far/(far-near).
然后看看不同的near的图像：

上面的是near=0.1，下面near=1，far都是20000，可以看到near变大，图像看上去更线性了，考虑到图像在near~far，高度0~1的一个矩形里，near靠近far，可以使这条近似直线不那么水平，避免变换的z大面积一样，出现Z-fighting现象。
但是near不能太大，否则近处的都被裁切了，看不到了。
前面只研究了横轴正方向，现在我们研究一下包含横轴负方向的。用于透视投影变换时，相机后面的一般都不考虑，如果判断裁切，点或线是可能在相机后面的。

可以看到横轴负方向跟正方向呈轴对称，靠近0，分别趋向正负无穷大，横轴正负无穷大时，都趋向far/(far-near)。
看个局部，比较清楚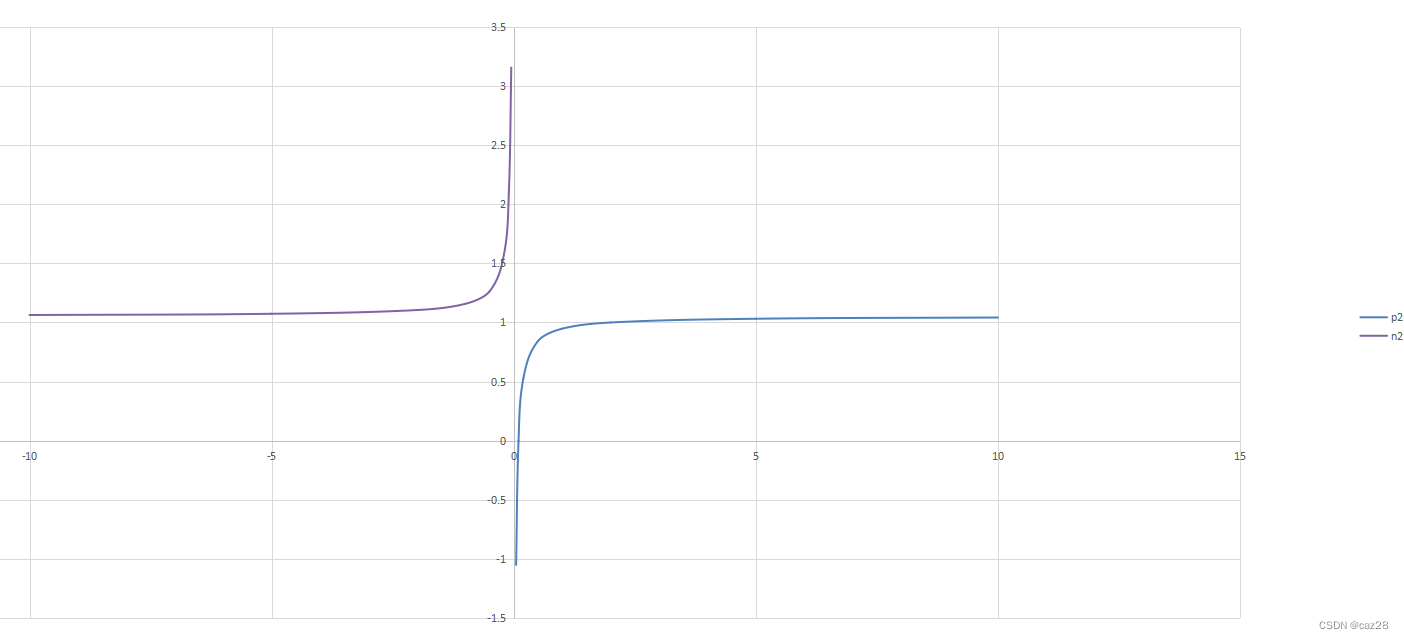

看整个函数图像，因为我们far=20000，所以线几乎是水平或垂直的直线，实际还是有一定斜率。

因为这个斜率很小，靠近1的浮点数也比较靠近0的地方浮点数少，所以出现多个不同z值变换后一样的问题，出现Z-fighting现象。
为了避免这个问题， Z reversed，也就是交换远近平面，NDC坐标中，近处是1，远处是0.
z反转后函数图像：

这个near=0.1，变换后是1，far=1，变换后是0。靠近0，分别趋向正负无穷大，横轴正负无穷大时，都趋向-near/(far-near)。
如果far比较大，下面是near=0.1，far=20000，整个看也比较还是那样，线比较平。

但far附近，转换后是0,0附近浮点数比较多，能弥补比较平这个问题。

参考：透视投影矩阵的一些概念 - BaoqingWu - 博客园