莱特飞行优化及其使用场景

一，莱特飞行

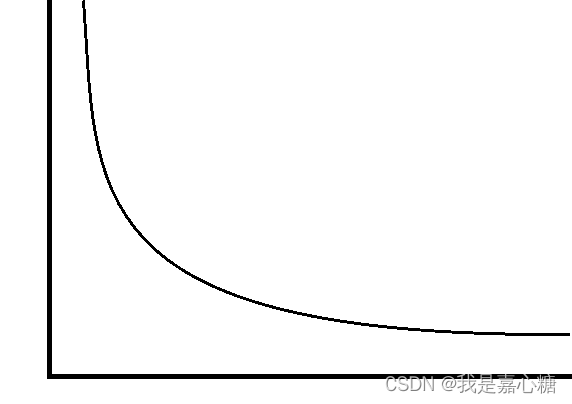
但是产生一个莱特飞行分布的随机数是比较难的，莱特只给出了一个积分，所以后面就有人提出了如何制造这样分布的随机数。

Mantegna
在1994年提出的一种用正态分布求解随机数的方法，有时也叫Mantegna方法，生成服从萊维分布的随机步长的方法如下：

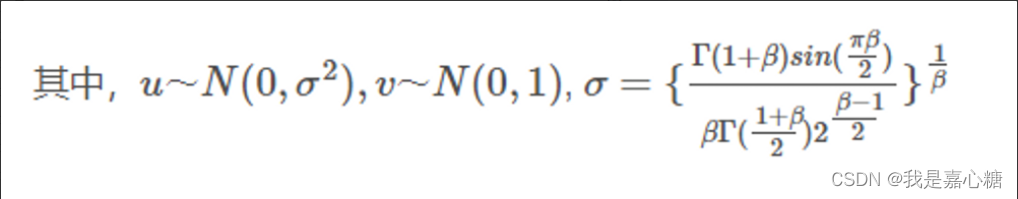
通常1≤β≤3，在实际应用中只用到s 作为一个随机数使用。

二，伽马函数

Γ（）函数则是伽马函数(gamma)

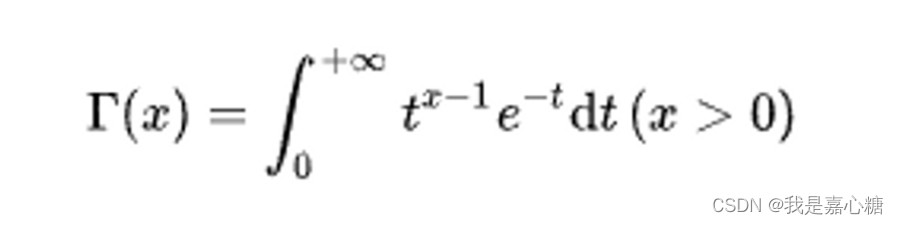
伽马函数的性质，第一第二还有第四点在考研数学里面也有使用到

伽马函数的代码实现

public static double gamma(double x, double setAbsRelaErr) {
        //setAbsRelaErr 相对误差绝对值
        //递归结束条件
        if(x < 0) {
            return gamma(x + 1, setAbsRelaErr) / x;
        }
        if(Math.abs(1.0 - x) < 0.00001) {
            return 1;
        }
        if(Math.abs(0.5 - x) < 0.00001) {
            return Math.sqrt(3.1415926);
        }

        if(x > 1.0) {
            return (x - 1) * gamma(x - 1, setAbsRelaErr);
        }
        double res = 0.0;
        double temp = 1.0;
        double check = 0.0;
        int i = 1;
        while(Math.abs((check - temp) / temp) > setAbsRelaErr){
            check = temp;
            temp *= i / (x - 1 + i);
            i++;
        }
        res = temp * Math.pow(i, x - 1);
        return res;
    }

三，莱特飞行应用于演化算法

莱特飞行应用于演化算法非常的简单，本质上就是获得一个随机数而已，在很多领域都有这种获得随机数的例子，常常直接使用均匀分布U(0，1)， 还有的使用高斯分布 N(0，1)，也有的直接使用混沌函数tent，来实现，这些用于演化算法的分布都是只有一个目的：保证种群的多样性！以及水论文！，首先使用的最出色的莱特飞行的算法就是布谷鸟算法（应该是开山鼻祖）

Cuckoo search for inverse problems and simulated-driven shape optimization ,Yang XS

然后后人继续发扬莱特飞行，将莱特飞行和容易收敛到局部最优的算法结合在一起，继续产生更多融合怪算法

• 刘紫阳,庞志华,陶佩,郑韩飞.记忆增强的莱维飞行引力搜索算法[J].计算机仿真,2022,39(01):312-317.
• 崔鸣,靳其兵.基于Levy飞行策略的灰狼优化算法[J].计算机与数字工程,2022,50(05):948-952+958.
• 丁瑞成,周玉成.引入莱维飞行与动态权重的改进灰狼算法[J/OL].计算机工程与应用:1-10[2022-12-05].http://kns.cnki.net/kcms/detail/11.2127.tp.20220916.1844.016.html
• 付华,许桐,邵靖宇.基于水波进化和动态莱维飞行的爬行动物搜素算法[J/OL].控制与决策:1-9[2022-12-05].DOI:10.13195/j.kzyjc.2022.0647.

随便在知网上面搜个levy就有一堆了，而且这也只是在国内演化算法领域的，还没算上实际使用这些算法的，所以说这个领域是个可以发论文的好地方，虽然在应用方面能发的论文等级不高，但是能毕业就很棒了。

这些融合怪算法使用levy飞行的时候常常是择劣，举个例子

杨晓倩,李琦,李豪欣,赵盟盟.基于改进正弦余弦算法的MIMO雷达相位编码信号集设计[J].电光与控制,2021,28(06):90-94.

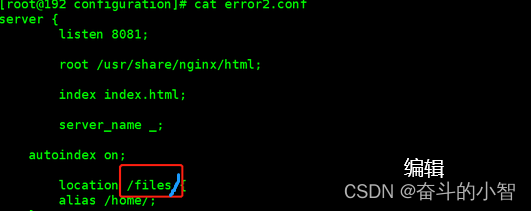
这篇文章用莱特飞行levy算法改进正弦余弦算法SCA

红色框框框住的地方就是莱特飞行改进的地方了，通过这种改进让容易收敛到局部最优的算法更好的探索

本人解答自己的疑惑：

为什么这些算法好像堆积木一样，这样有什么意义吗？拼两拼就是创新呢？

其实每个算法在不同问题的效果是不一样的。最近看了正弦余弦的文章。SCA: A Sine Cosine Algorithm for solving optimization problems里面有个说法就是

尽管最近在这个领域提出了大量的算法，但这里仍然存在一个基本问题，即我们是否需要以及为什么需要更多的优化技术。这个问题可以参考所谓的无免费午餐（NFL）定理来回答[60]。这个定理从逻辑上证明，没有人能提出一个解决所有优化问题的算法。这意味着，算法在解决一组特定问题时的成功并不能保证解决所有不同类型和性质的优化问题。换句话说，当考虑所有优化问题时，尽管在优化问题的子集上具有优异的性能，但所有优化技术的平均性能都相同。NFL定理允许研究人员提出新的优化算法或改进/修改现有算法，以解决不同领域的问题子集

所以说，我们现在对这些演化算法的改进其实也是有用的，拼接两下也确实可能会带来实验效果的提升，所以这也是创新的一种，虽然最后可能写出来的东西并不能应用落地，但是至少不是垃圾就是了。