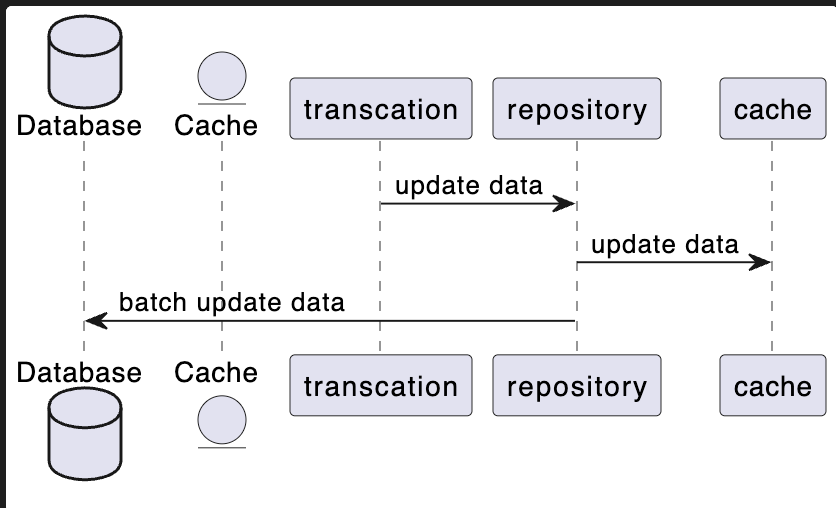
最小二乘问题:![]()
采用适当的方法可将约束优化问题转换为无约束优化问题;

无约束优化问题的最优性条件

需要说明的是,由于二阶梯度可以取0,我们由一元函数的知识可以知道,它是必要条件而非充分条件,当把等号去掉,就变为充分条件
证明:用反证法


充分条件
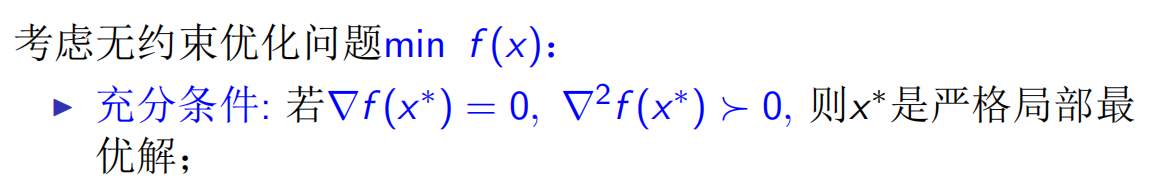

对于最优化问题的求解,其基本思路是,(1)首先找一个x_k,判断x_k是否为最优解;(2)如果x_k不是最优解,找下一个x_k


信赖域方法更像是线搜索方法反过来,即先确定步长的范围,再确定方向,比较复杂。
(基于线搜索的)下降算法基本思路

关键要素:终止条件、下降方向、步长



线搜索方法:
当f(x)为简单函数时,我们可以通过表示为a的函数,通过梯度为0,求出a
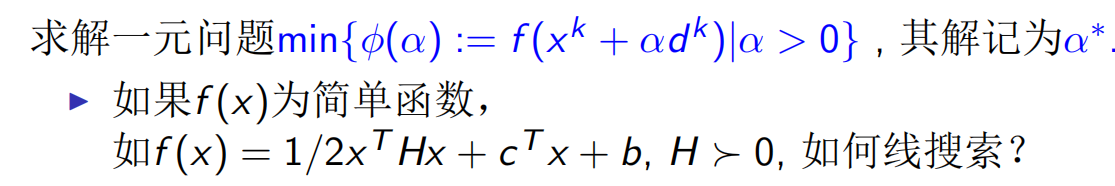
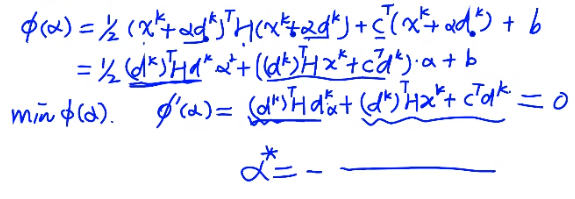
基于搜索区间的直接搜索法
当f是复杂函数时,可以采取基于搜索区间的直接搜索法。首先初始化一个区间,然后在区间中选取两个点,根据函数值的大小缩小区间。很显然,这种方法只适用于单谷。
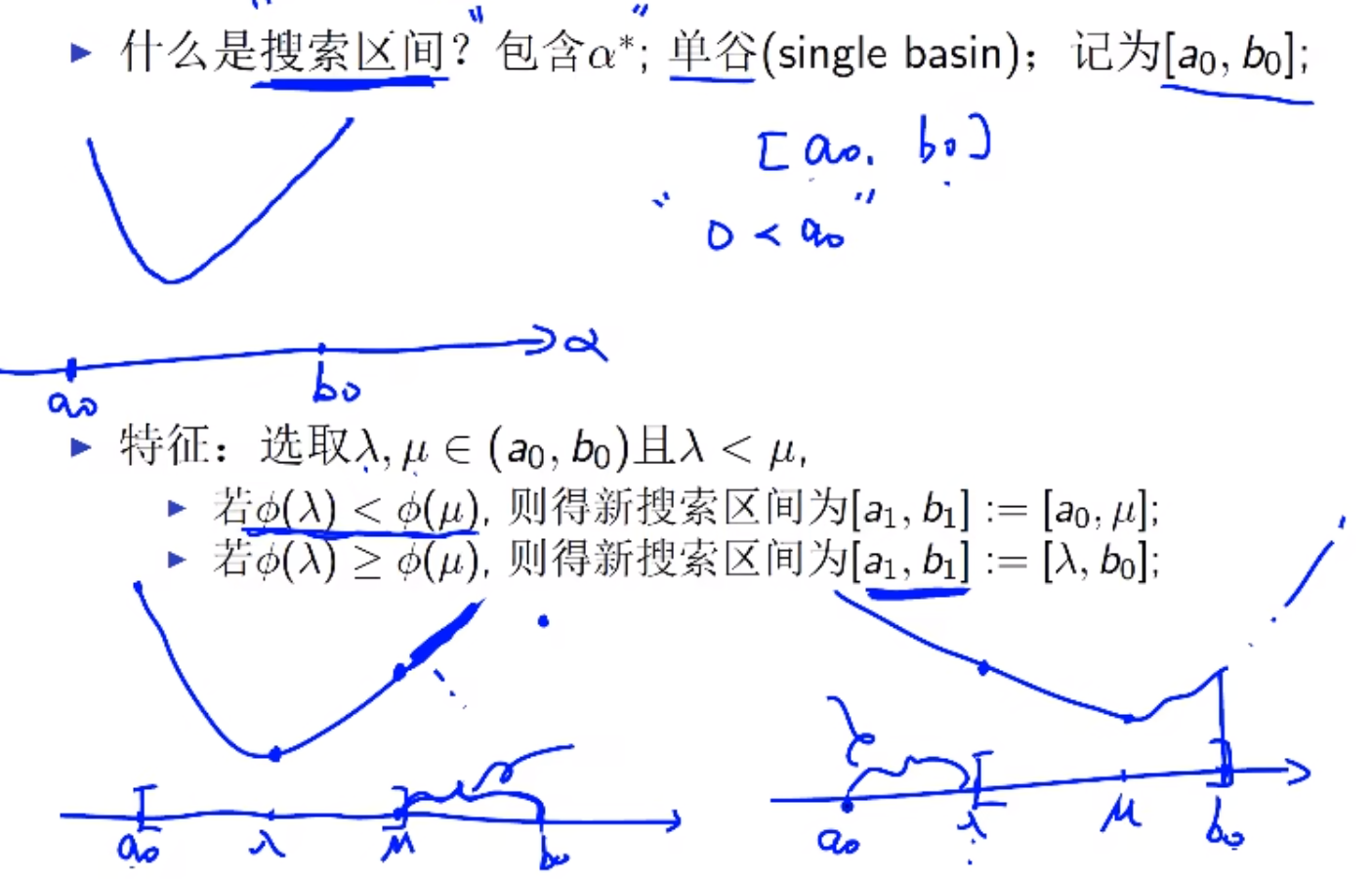
均匀搜索法:
通过计算N-1个函数点的值将区间缩小为原来的2/N

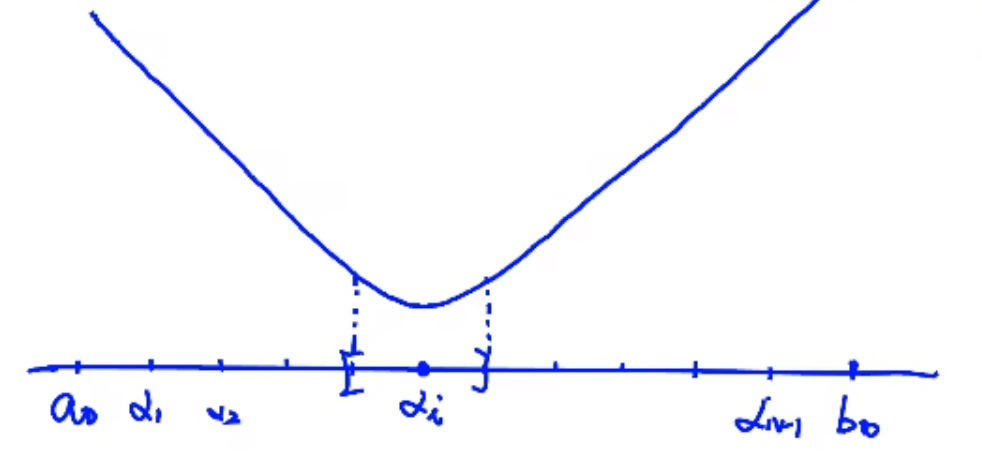
黄金区间法(0.618法):
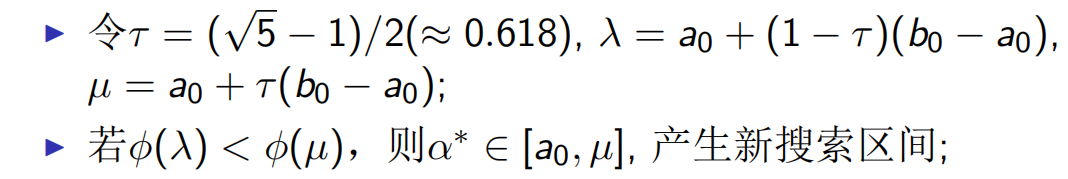
黄金分割法第一次需要计算2个点的函数值,而对于第二次,其中一个点在第一次已经计算过(1-0.618)/0.618=0.618(换成(根5-1)/2也满足) ,只需要计算一个点的函数值

基于导数信息的二分法:

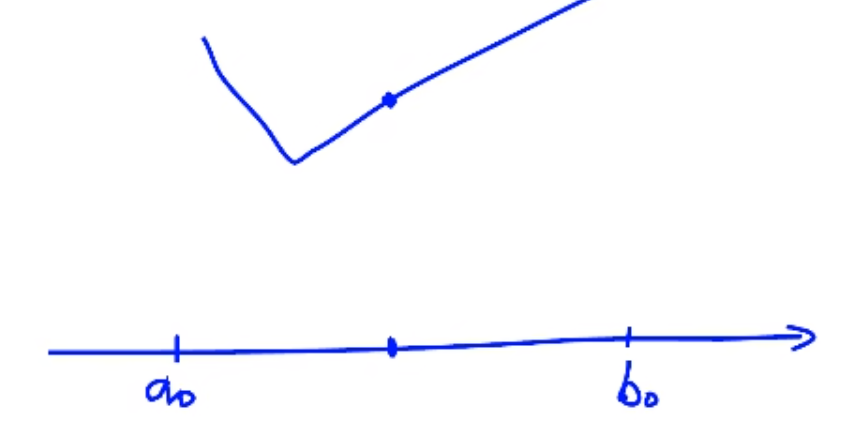
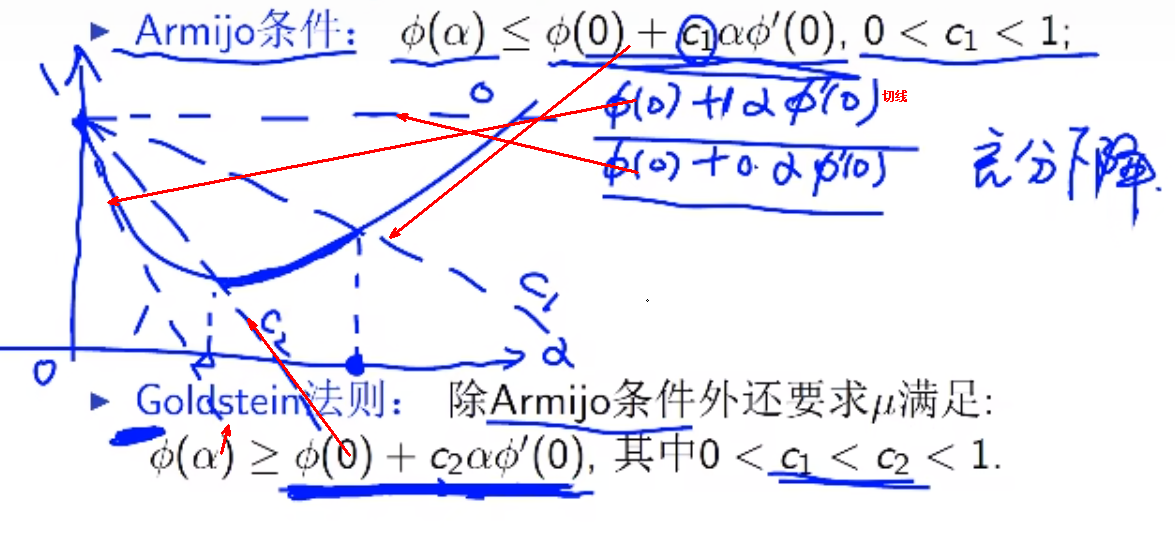
非精确线搜索Inexact linear search