1. 作者介绍
2. K近邻算法与决策树算法介绍
- 2.1 K近邻（KNN）简介
- 2.2 决策树算法简介
- 2.3 MNIST数据集简介：
3. K近邻算法和决策树算法在Mnist数据集分类实验对比
- 3.1 K近邻算法对Mnist数据集分类实验
- 3.2 K近邻代码实现
- 3.3 决策树算法实验
- 3.4 决策树代码实现
- 3.5 实验结果对比

1. 作者介绍

郝特吉，男，西安工程大学电子信息学院，2022级研究生
研究方向：机器视觉与人工智能
电子邮件：826844822@qq.com

路治东，男，西安工程大学电子信息学院，2022级研究生，张宏伟人工智能课题组
研究方向：机器视觉与人工智能
电子邮件：2063079527@qq.com

2. K近邻算法与决策树算法介绍

2.1 K近邻（KNN）简介

K近邻是一种经典且简单的监督学习方法，既能够用来解决分类问题，也能够解决回归问题。
原理：当对测试样本进行分类时，通过扫描训练样本集，找到与该测试样本最相似的个训练样本，根据这个样本的类别进行投票确定测试样本的类别。
基本要素：
1.分类决策规则
一般采用少数服从多数的投票制规则，但可以根据具体问题，实现分段距离加权的方式进行，本次KNN主要采用多数服从少数的投票制规则。

2.距离度量
Lp 距离：
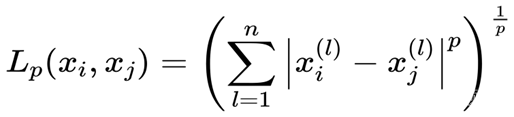
在这里插入图片描述

p = 1 ，为曼哈顿距离
p = 2，为欧氏距离
p = ∞ ，为各个坐标距离的最大值
本次实验采用欧氏距离
3.k 值的选择
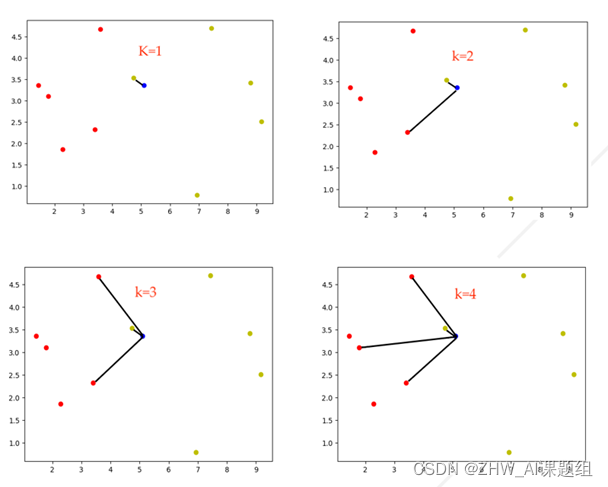
在这里插入图片描述
本次实验主要对k的值为15的准确率变化进行研究

2.2 决策树算法简介

决策树，是一个类似流程图的树形结构，树内部的每一个节点代表对一个特征的测试，树的分支代表该特征的每一个测试结果，而树的每一个叶子节点代表一个类别。树的最高层是就是根节点。
举个例子，以面试机器学习算法工程师为例，下图说明了如何利用决策树进行面试。
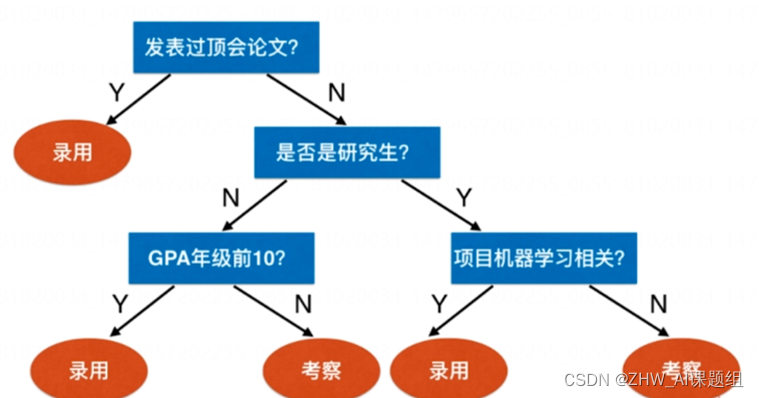
在这里插入图片描述
从中不难总结出决策树的主要问题就是：
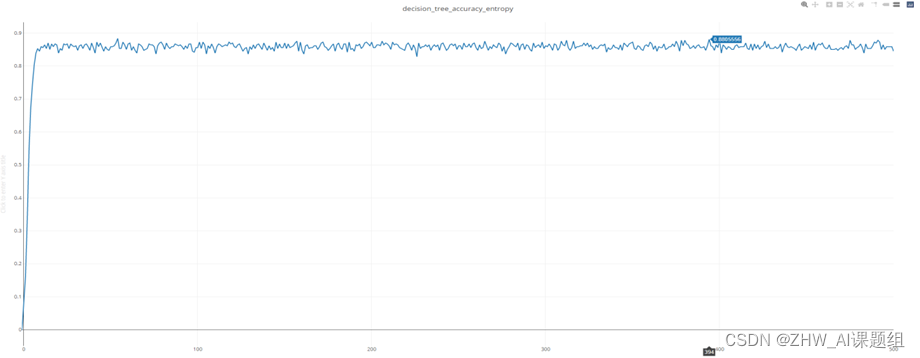
1.哪个维度划分？
2.该维度的哪个值划分？

决策树算法的策略
1. 信息熵：
代表随机变量不确定度，熵越大，数据不确定性越高。熵越小，数据不确定性越低。目的：希望在树节点划分后使信息熵降低。
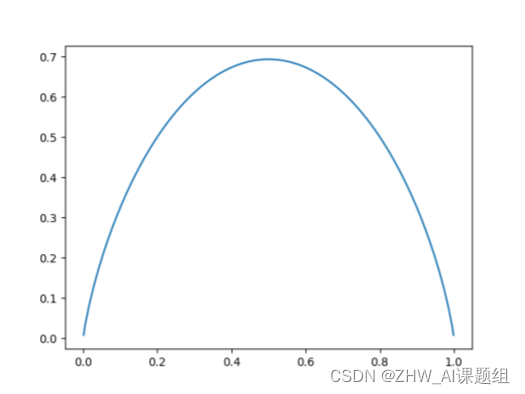
在这里插入图片描述

二分类信息熵曲线如上图所示。
**2.基尼指数（基尼不纯度）：**表示在样本集合中一个随机选中的样本被分错的概率。
目的：希望在划分后使得基尼指数降低。

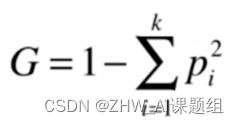
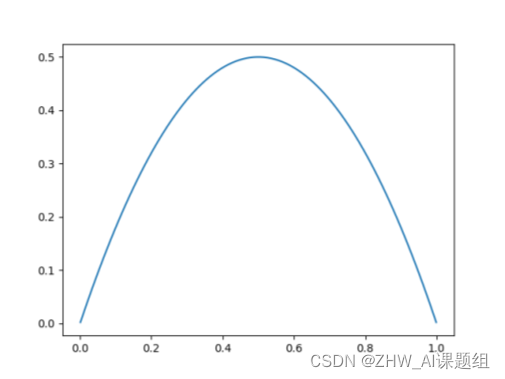
二分类基尼系数曲线如上图所示

2.3 MNIST数据集简介：

MNIST是一个手写体数字 0-9 的图片数据集，一共统计了来自250个不同的人手写数字图片，其中，每张图片为：28*28的灰度图片，对应标签采用 one-hot -vector 形式编码
Mnist数据集官网：http://yann.lecun.com/exdb/mnist/

MNIST数据集的下载内容：
在这里插入图片描述
使用后自动解压为：

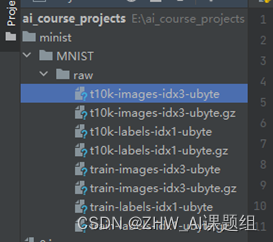
train_and_test 划分：
Train_datas:60000张
Test_datas:10000张
数据集划分
对数据集进行可视化，下图为Mnist数据集中的图和标签

下图为Mnist数据集在FDA降维下的分布

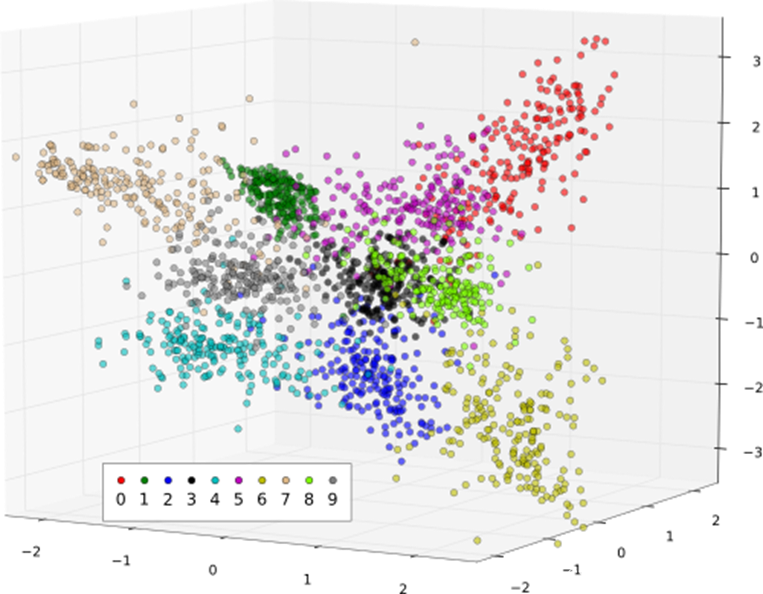
3. K近邻算法和决策树算法在Mnist数据集分类实验对比

3.1 K近邻算法对Mnist数据集分类实验

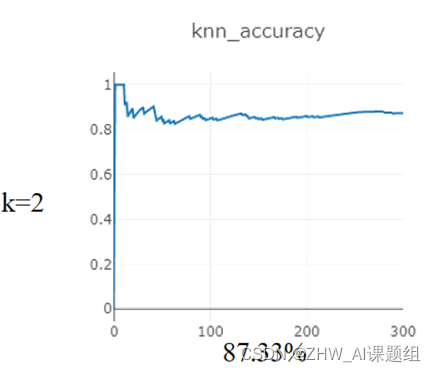
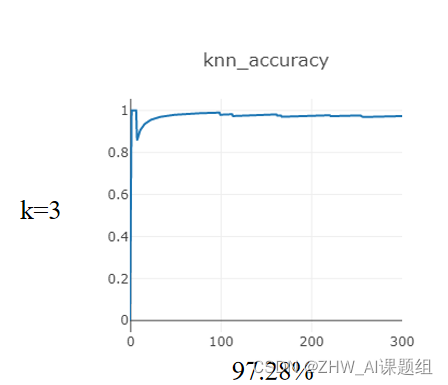
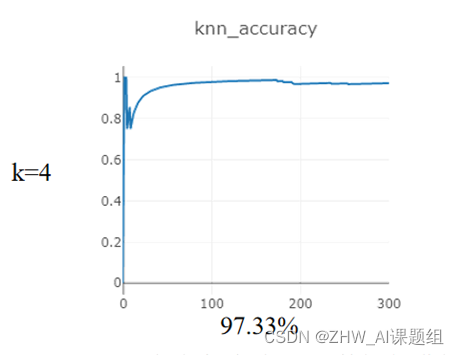
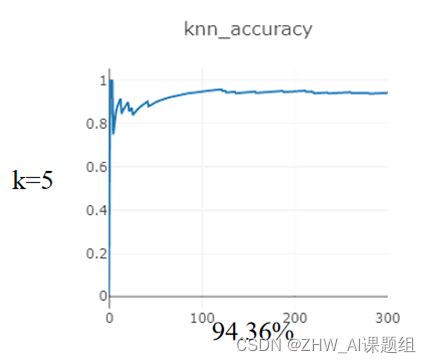
本次实验对Mnist数据集进行分类，在距离度量为：欧式距离，分类决策规则为：少数服从多数的基础上，研究：在使用KNN算法达到最高准确率的情况下，K在1-5之间的取值。
在测试集（10000）sample：300个样本
在训练集（60000）sample：10000个样本
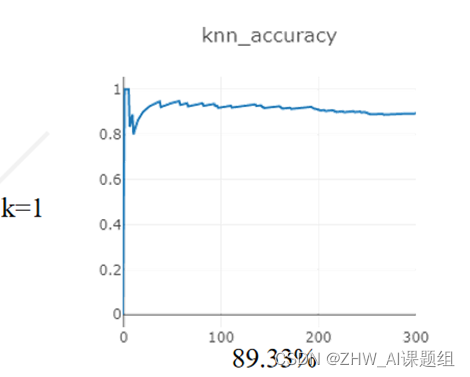
在这里插入图片描述

3.2 K近邻代码实现

import torch
import numpy as np
from torch.utils.data import DataLoader
from torch import nn, optim
from math import sqrt
from torchvision import transforms, datasets
import visdom
from collections import Counter

viz = visdom.Visdom()
batchsize_all = 10000
batchsize = 1

minist_train = datasets.MNIST('minist', True, transform=transforms.Compose([
    transforms.ToTensor()
]), download=True)
minist_train = DataLoader(minist_train, batch_size=batchsize_all, shuffle=True)

minist_test = datasets.MNIST('minist', True, transform=transforms.Compose([
    transforms.ToTensor()
]), download=True)
minist_test = DataLoader(minist_test, batch_size=batchsize, shuffle=True)

# X = []
# Y = []
# for batchidx, (X_train, Y_train) in enumerate(minist_train):
#     X.append(X_train)
#     Y.append(Y_train)
# print(len(Y))
#
# X1 = []
# Y1 = []
# for batchidx, (X_test, Y_test) in enumerate(minist_test):
#     X1.append(X_test)
#     Y1.append(Y_test)
# print(len(Y1))

# x, y = next(iter(minist_train))

# print('x:', x.shape)
# print(y.shape)
# print(y)
acc_sum = 0
sum = 0

viz.line([0], [-1], win='knn_accuracy', opts=dict(title='knn_accuracy'))


k = int(input('请输入选择最近邻的个数：'))
for _ in range(300):
    for batchidx, (X_train, Y_train) in enumerate(minist_train):
        #KNN
        distances = []
        x_test, y_test = next(iter(minist_test))
        viz.images(x_test, nrow=1, win='x', opts=dict(title='x'))
        # print(x_test.shape)
        # print()



        for x_train in X_train:
            x_train = x_train.unsqueeze(0)
            # print(x_train.shape)
            #k_nn
            pp = pow(x_train - x_test, 2).view(1, 28*28)
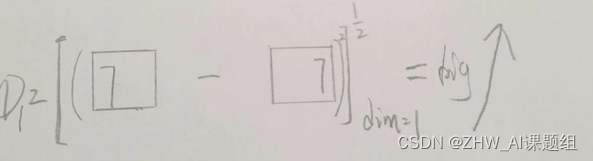
            D = sqrt(pp.sum(dim=1))
            # print(pp)
    #         D = sqrt(np.sum(((x_train - x_test)**2).view(28*28)))  #欧拉距离
            distances.append(D)
        nearest = np.argsort(distances)  #索引排序从近到远
        # print(nearest)
        k_top = [Y_train[i] for i in nearest[:k]]  #前K个标签值
        nears_value = [X_train[i] for i in k_top]
        votes = Counter(k_top)  #得到投票结果
        pre_label = votes.most_common(1)[0][0]  #预测最可能结果
        sum += 1
        if pre_label == y_test:   #计算分类准确率
            acc_sum += 1
        accuracy = acc_sum / sum
        print('准确率为：', accuracy)
        np_pre_label = pre_label.numpy()
        viz.line([accuracy], [sum], win='knn_accuracy', update='append')
        viz.text(str(np_pre_label), win='pre_label', opts=dict(title='prelabel'))
        break

    # print(pre_label)
    # print(y_test)

3.3 决策树算法实验

本次实验在scikit-learn中集成的决策树CART下进行：
发现：
1.信息熵计算相对较慢，
2.scikit-learn中默认为基尼系数
3.没有特别大的差距
决策树的局限性：严重的过拟合
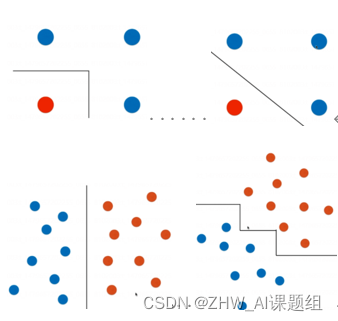
在这里插入图片描述
下图为1-500个不同深度gini分类准确率曲线

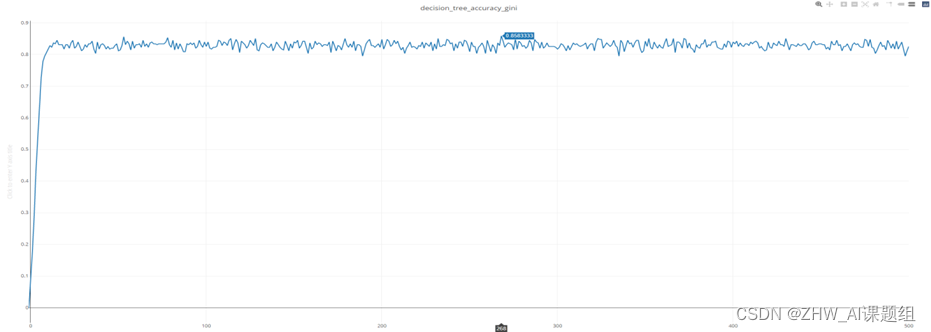
下图为1-500不同深度entropy分类准确率

3.4 决策树代码实现

from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
import visdom
import numpy as np

mnist = load_digits()
x, test_x, y, test_y = train_test_split(mnist.data, mnist.target, test_size=0.2, random_state=40)

viz = visdom.Visdom()
viz.line([0], [-1], win='decision_tree_accuracy_entropy', opts=dict(title='decision_tree_accuracy_entropy'))
# viz.line([0], [-1], win='decision_tree_accuracy_gini', opts=dict(title='decision_tree_accuracy_gini'))

for i in range(500):
    model = DecisionTreeClassifier(max_depth=i+1, criterion="entropy")
    # model = DecisionTreeClassifier(max_depth=i + 1, criterion="gini")
    model.fit(x, y)
    pre = model.predict(test_x)
    acc = np.sum(pre == test_y) / pre.size
    print('accuracy：', acc)
    viz.line([acc], [i+1], win='decision_tree_accuracy_entropy', update='append')
    # viz.line([acc], [i + 1], win='decision_tree_accuracy_gini', update='append')

3.5 实验结果对比

在本次针对Mnist数据集，分别采用KNN和决策树算法进行分类的对比实验中发现KNN的分类准确率优于决策树！
KNN_average_accuracy = 93.126% > 88.055% = decision_tree_max_accuracy
why？
分析：
Mnist数据集的样本的特殊之处：它是一个250多人手写的数字体，且在Mnist数据集官网上发布的是一个经过居中和裁边处理过的28*28的灰度图。

如果没有居中和裁边处理：
在这里插入图片描述
经过居中裁边处理：

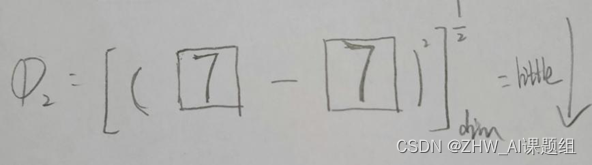
可以看出，经过裁边的mnist数据集非常适合运用KNN将其区分开来
而灰度图起作用在计算距离时，只考虑其图像的空间分布，没有将颜色通道干扰考虑在内，这样就更高效更有针对性的计算出分布之间的距离！
第二个原因则是，在是决策树本身的局限性和mnist数据集特性的共同作用：
我们可以从mnist的降维分布看出，总会有一些不同类的分布距离十分靠近：
在这里插入图片描述
观察准确率减少时发现分类错误的样本：

总结：
但是决策树在高维空间中对决策边界的划分，总是有一部分很难被完美区分，而KNN却可以根据K值的选择一定程度上将样本做出正确划分！这就是为什么KNN在MNIST数据集上的分类性能要优于决策树的主要原因！