242.有效的字母异位词

1.题目描述

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。

注意：若 s 和 t 中每个字符出现的次数都相同，则称 s 和 t 互为字母异位词。

示例：
输入: s = “anagram”, t = “nagaram”
输出: true

输入: s = “rat”, t = “car”
输出: false

详情leetcode链接

2.题解

先看思路哦！

class Solution {
    /**
     * 思路：需要一个额外的数组记录两个字符串每个字母出现的次数，一个次数增加，
     *       一个次数减少；若最后每个数组上每个数字都中和为0则为字母异位词。
     *     1.因为都是小写字母，所以需要定义一个数组record来记录每个字母出现的次数；
     *     2.因为字符a到字符z的ASCII也是26个连续的数，所以数组大小为 26，初始化为0；
     *     3.需要把字符映射到数组也就是哈希表的索引下标上：因为字符a到字符z的ASCII是
     *  26个连续的数值，所以字符a映射为下标0，相应的字符z映射为下标25。
     *     4.再遍历 字符串s的时候，只需要将 s[i] - ‘a’、‘b’等所在的元素做+1 操，同
     *  样在遍历字符串t的时候，对t中出现的字符映射哈希表索引上的数值再做-1的操作。 
     *     5.最后record数组如果有的元素不为零0，即字符串s和t一定是谁多了字符或者谁少
     *  了字符，return false。若record数组所有元素都为零0，说明字符串s和t是字母异位
     *  词，return true。
     * 时间复杂度：O(m+n),分别遍历了字符串s和t，长度设为 m 和 n（补充：因为数组长度与输入参数无关且为常量可看作O(1)可忽略不计,这里的m和n是和输入字符串长度有关，所以为m+n）
     * 空间复杂度：O(1)
     *     
     *
     */
    public boolean isAnagram(String s, String t) {
        int[] record = new int[26];
		//例如字符串s="aee"，字符串t="eae"
		//s.charAt(a)-'a'=0,即recored数组的第一个位置，刚好与a~z相映射
        for (int i = 0; i < s.length(); i++){
            record[s.charAt(i)-'a']++; //charAt()即返回指定索引处的字符，举例字符a返回97。并不需要记住字符a的ASCII，只要求出一个相对数值就可以了
        }

        for (int i = 0; i < t.length(); i++){
            record[t.charAt(i)-'a']--;
        }

        for (int count : record){
            if (count != 0){  // record数组如果有的元素不为零0，说明字符串s和t 一定是谁多了字符或者谁少了字符。
                return false;
            }
        }

        return true; // record数组所有元素都为零0，说明字符串s和t是字母异位词
    }
}

349.两个数组的交集

1.题目描述

给定两个数组 nums1 和 nums2 ，返回它们的交集。输出结果中的每个元素一定是唯一的。我们可以不考虑输出结果的顺序。

示例：
输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]
解释：[4,9] 也是可通过的

详情leetcode链接

2.题解

先看思路哦！

class Solution {

    /**
     * 思路：哈希set
     *      题目中提到输出结果中的每个元素一定是唯一的，即输出的结果的去重的， 同时可以不考虑输出结果的顺序，所以用哈希set做比较合适
     *      首先遍历数组nums1，将nums1映射到set1中。
     *      接着遍历数组2的过程中判断哈希表set1中是否存在该元素，若存在则放到reSet(用于返回的set)中，最后将结果集转为数组返回。
     * 注意：此题也可以使用数组来做哈希的题目，是因为题目都限制了数值的大小。如果本题没有限制数值的大小，就无法使用数组来做哈希表了。
     * 时间复杂度：O(m + n)：假设数组nums1长度为m，nums长度为n。分别遍历
     * 空间复杂度：O(m): 定义了两个set，其大小取决于nums的大小
     *
     */
    public int[] intersection(int[] nums1, int[] nums2) {
        if (nums1 == null || nums1.length == 0 || nums2 == null || nums2.length == 0) {
            return new int[0];
        }
        Set<Integer> set1 = new HashSet<>();
        Set<Integer> reSet = new HashSet<>();
        //遍历nums1映射到set1
        for (int i: nums1) {
            set1.add(i);
        }

        //遍历nums2过程中判断set1中是否存在该元素，存在放到reSetzh
        for (int i : nums2){
            if (set1.contains(i)){
                reSet.add(i);
            }
        }

        //将结果集转为数组返回
        return reSet.stream().mapToInt(x->x).toArray();

        // //方法2：将结果集转为数组返回
        // int[] array = new int[reSet.size()];
        // int j = 0;
        // for (int i : reSet){
        //     array[j++] = i;
        // }
        // return array;

    }
}

202.快乐数

1.题目描述

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1。
如果这个过程结果为 1，那么这个数就是快乐数。
如果 n 是快乐数就返回 true ；不是，则返回 false 。

示例 1：
输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

示例 2：
输入：n = 2
输出：false

详情leetcode链接

2.题解

思路(官方题解啊！看了好几遍真难)

根据题意确定边界：（1）最终会得到1；（2）最终会进入循环
举例1，例如7——>7²=49——>4²+9²=97…（不断循环此过程），如图直到1
举例2，从 116开始。通过反复通过平方和计算下一个数字，我们最终得到 58，再继续计算之后，我们又回到 58。由于我们回到了一个已经计算过的数字，可以知道有一个循环，因此不可能达到 1。
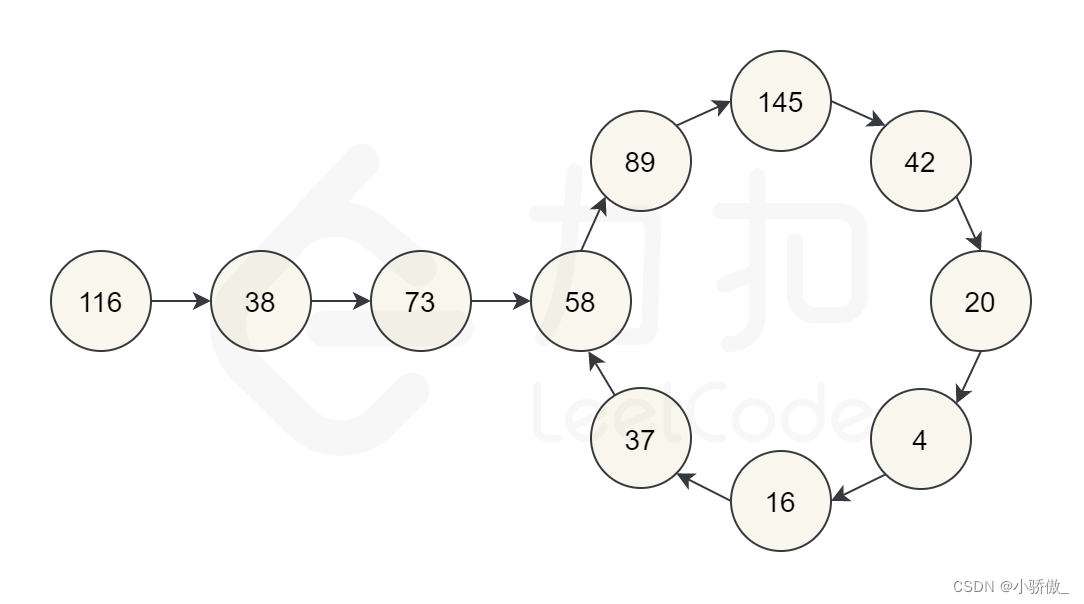
所以根据穷举，猜测会有以下三种可能。
最终会得到 11。
最终会进入循环。
值会越来越大，最后接近无穷大。
对于第三种情况的思考：我们怎么知道它会继续变大，而不是最终得到 1 呢？可以仔细想一想，每一位数的最大数字的下一位数是多少。
对于 3位数的数字，它不可能大于 243。这意味着它要么被困在 243以下的循环内，要么跌到 1。4 位或 4 位以上的数字在每一步都会丢失一位，直到降到 3 位为止。所以我们知道最坏的情况下，算法可能会在 243 以下的所有数字上循环，然后回到它已经到过的一个循环或者回到 1。但它不会无限期地进行下去，所以我们排除第三种选择。

算法

算法分为两部分，我们需要设计和编写代码。

给一个数字 n，它的下一个数字是什么？
按照一系列的数字来判断我们是否进入了一个循环。

第 1 部分我们按照题目的要求做数位分离，求平方和。

第 2 部分可以使用哈希集合完成。每次生成链中的下一个数字时，我们都会检查它是否已经在哈希集合中。
如果它不在哈希集合中，我们应该添加它。
如果它在哈希集合中，这意味着我们处于一个循环中，因此应该返回 false。

注意： 我们使用哈希集合而不是向量、列表或数组的原因是因为我们反复检查其中是否存在某数字。检查数字是否在哈希集合中需要 O(1)的时间，而对于其他数据结构，则需要 O(n)的时间。

代码实现

/**
 * 202.快乐数
 * 1）给定一个数n，获取下一个数是什么？
 * 2）按照一系列的数字来判断我们是否进入了一个循环
 * 时间复杂度：O(logn)
 * 空间复杂度：O(logn)
 */
class Solution {

    public static int getNext(int n){
        int totalSum = 0;
        while (n>0){
            int d = n % 10;//取余数获得个位上的数字
            n = n / 10;//取商获得十位上的数字
            totalSum += d*d;
        }
        return totalSum;
    }

    public static boolean isHappy(int n){
        Set<Integer> seen = new HashSet<>();//利用set判断重复
        while (n != 1 &&  !seen.contains(n)){
            seen.add(n);
            n = getNext(n);
        }
        return n==1;
    }
}