本专栏包含信息论与编码的核心知识，按知识点组织，可作为教学或学习的参考。markdown版本已归档至【Github仓库：https://github.com/timerring/information-theory 】或者公众号【AIShareLab】回复 信息论 获取。

文章目录

分集
- 分集的概念
- 分集的方法
- - 空间分集
  - 时间分集
  - 频率分集
  - 多径分集
- 路径合并方式
- - 选择式合并
  - 等增益合并
  - 最大比值合并
- Alamouti空时分组码(STBC)简介

分集

分集的概念

分集是一种抗衰落技术。原理是利用两个以上信号传送同一个信息，并且这些不同信号的衰落相互独立。在接收端以适当方式将这些信号合并利用，以降低合成信号电平起伏，减小各种衰落对接收信号的影响，进而恢复信息。

设同一信息经过两路信号传输, 包络为 $v_{1}(t)$ 和 $v_{2}(t)$ , 设 $u_{0}$ 为门限电平, 当小于门限电平时则产生错误, 令

$P[v_{1}(t) \lt u_{0}] = P[v_{1}(t) \lt u_{0}] = 10^{-3}$

若 $v_{1}(t)$ 和 $v_{2}(t)$ 独立, 则二者同时小于 $u_{0}$ 的概率为

$P[v_{1}(t) \lt u_{0}, v_{2}(t) \lt u_{0}]=10^{-3} \times 10^{-3}=10^{-6} \ll 10^{-3}$

此时若同时利用 $v_{1}(t)$ 和 $v_{2}(t)$ 来恢复信息，则可减少错

若 $v_{1}(t)$ 和 $v_{2}(t)$ 完全相关则 :
$P[v_{1}(t) \lt u_{0}, v_{2}(t) \lt u_{0}]=10^{-3}$
结论: 要达到抗多径效果, 要求 $v_{1}(t)$ 和 $v_{2}(t)$ 统计独立或不相关或弱相关.

分集的方法

获得不相关路径信号的方法:

空间分集

采用多天线接收同一信号, 相邻天线间距离大于载波波长 3 倍以上。（注：理论最小值为 $\lambda / 2$ ）。

CCIR建议为了获得满意的分集效果, 移动单元两天线间距大于 0.6 个波长, 即 $\mathrm{d}>0.6 \lambda$ , 并且最好选在 $\lambda / 4$ 的奇数倍附近。

分集天线数(分集重数)越多，性能改善越好。当分集重数多到一定数时，分集重数继续增多，性能改善量将逐步减小。

结论:分集重数在2~4重比较合适。

空间分集还有两类变化形式:

极化分集: 它利用在同一地点两个极化方向相互正交的天线发出的信号可以呈现不相关的衰落特性进行分集接收，即在收发端天线上安装水平、垂直极化天线，就可以把得到的两路衰落特性不相关的信号进行极化分集。
- 优点:结构紧凑、节省空间;
- 缺点:由于发射功率要分配到两副天线上，因此有3dB的损失。
角度分集: 由于地形、地貌、接收环境的不同，使得到达接收端的不同路径。

信号可能来自不同的方向，这样在接收端可以采用方向性天线,分别指向不同的到达方向。而每个方向性天线接收到的多径信号是不相关的。

时间分集

不同时刻发送相同信号，时间间隔大于移动信道的相干时间，有效抵抗快衰落的分集技术。

注意：时间分集对于静止状态的移动台是无效果的。一般和空间分集结合,大多应用于快速移动的场合。

频率分集

采用不同频率载波传送同一信息, 不同载波频率差大于信道相干带宽。

在移动通信中, 当工作频率在 900 MHz 频段, 典型的最大多径时延差为 $\mu s$ , 此时有
$\Delta f>B_{c}=\frac{1}{\Delta \tau_{m}}=\frac{1}{5 \times 10^{-6}}=200 \mathrm{kHZ}$

因此, 若在该系统中利用频率分集, 载波频率差大于 200 kHz 。

优点是在接收端可以减少接收天线及相应设备的数量，
缺点是要占用更多的频带资源，并且在发送端可能需要采用多个发射机。

多径分集

采用扩频信号传送消息，在接收端将不同时延的多径信号分离

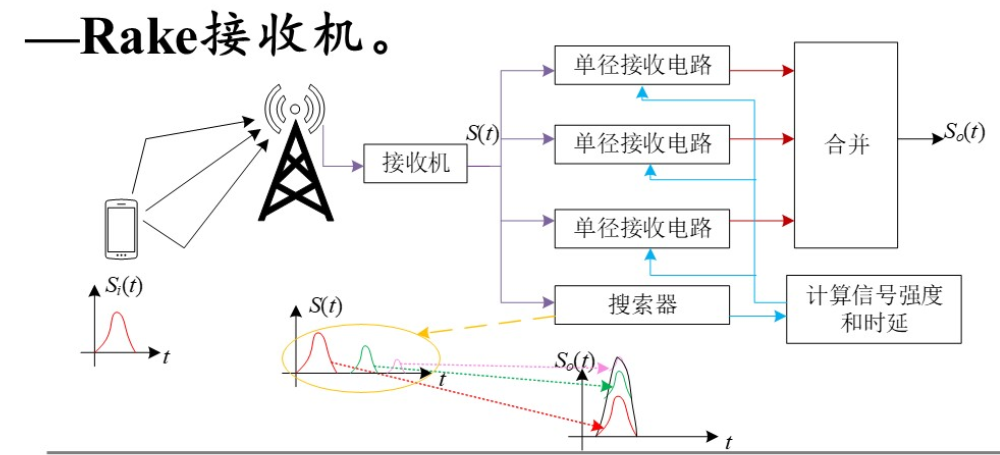
路径合并方式

分集接收包含有两重含义:

分散接收，使接收端能得到多个携带同一信息的、统计独立的衰落信号;
集中处理，即接收端把收到的多个统计独立的衰落信号进行适当的合并，从而降低衰落的影响，改善系统性能。

假设 N 个独立衰落信号分别为 $r_{1}(t), r_{2}(t), \ldots, r_{N}(t)$ , 则合并器输出为
$r(t)=a_{1} r_{1}(t)+a_{2} r_{2}(t) \cdots+a_{N} r_{N}(t)=\sum_{i=1}^{N} a_{i} r_{i}(t)$
式中, $a_{i}$ 为第 i 个信号的加权系数。选择不同的加权系数, 就可构成不同的合并方式。

常用的三种合并方式是：选择式合并、等增益合并和最大比值合并。表征合并性能的参数有平均输出信噪比、合并增益等。

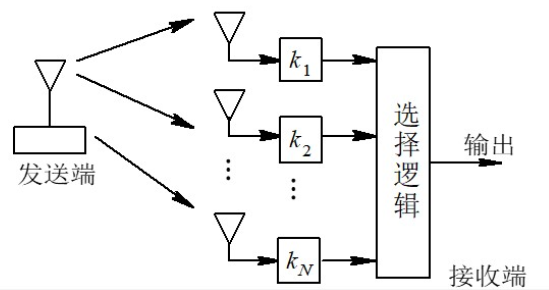
选择式合并

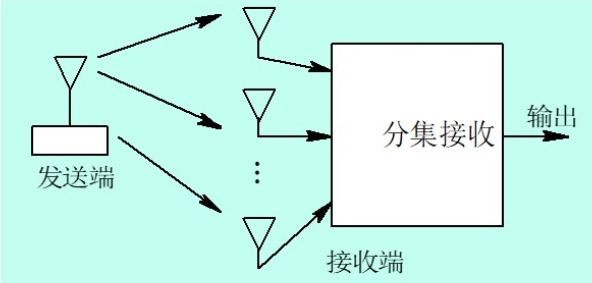
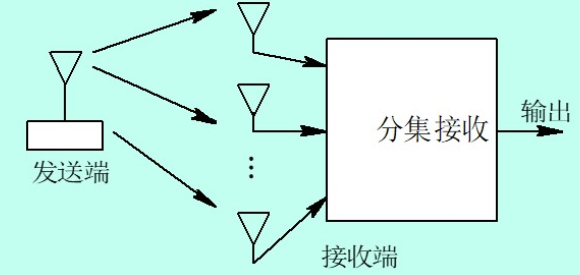
选择式合并是所有合并方式中最简单的一种。其原理是检测所有接收机输出信号的信噪比，选择其中信噪比最大的那一路信号作为合并器的输出，其原理图如图所示

选择式合并的平均输出信噪比为
$\overline{r_{M}}=\overline{r_{0}} \sum_{k=1}^{N} \frac{1}{k}$
合并增益为
$G_{M}=\frac{\overline{r_{m}}}{\overline{r_{0}}}=\sum_{k=1}^{N} \frac{1}{k}$
式中, $\overline{r_{M}}$ 为合并器平均输出信噪比, $\overline{r_{0}}$ 支路信号最大平均信噪比。可见, 对选择式分集, 每增加一条分集路径 , 对合并增益的贡献仅为总分集支路数的倒数倍。

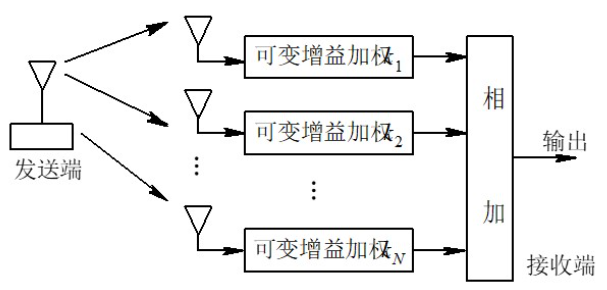
等增益合并

等增益合并原理如图所示。当加权系数 $\boldsymbol{k}_{1}=\boldsymbol{k}_{2}=\ldots=\boldsymbol{k}_{N}$ 时, 即为等增益合并。假设每条支路的平均噪声功率是相等的, 则等增益合并的平均输出信噪比为
$\overline{r_{M}}=\bar{r}[1+(N-1) \frac{\pi}{4}]$
合并增益为
$G_{M}=\frac{\overline{r_{M}}}{\bar{r}}=1+(N-1) \frac{\pi}{4}$
式中, $\bar{r}$ 为合并前每条支路的平均信噪比。

最大比值合并

最大比值合并方法最早是由Kahn提出的, 其原理可参见上图。最大比值合并原理是各条支路加权系数与该支路信噪比成正比。信噪比越大, 加权系数越大, 对合并后信号贡献也越大。若每条支路的平均噪声功率是相等的, 可以证明, 当各支路加权系数为
$\boldsymbol{k}_{\boldsymbol{i}}=\frac{A_{i}}{\sigma^{2}}$
时, 分集合并后的平均输出信噪比最大。式中, $\mathbf{A}_{\mathrm{i}}$ 为第 $\mathrm{i}$ 条支路信号幅度, $\boldsymbol{\sigma}^{2}$ 为每条支路噪声平均功率。

最大比值合并后的平均输出信橾比为
$\overline{r_{M}}=N \bar{r}$
合并增益为
$G_{M}=\frac{\overline{r_{M}}}{\bar{r}}=N$
可见, 合并增益与分集支路数 $\mathbf{N}$ 成正比。

分集接收信号的三种合并方式，下列哪种是按照性能由好到坏的排列? B

A. 最佳选择式、等增益合并、最大比合并

B. 最大比合并，等增益合并，最佳选择式

C. 等增益合并、最大比合并、最佳选择式

D. 最大比合并，最佳选择式、等增益合并

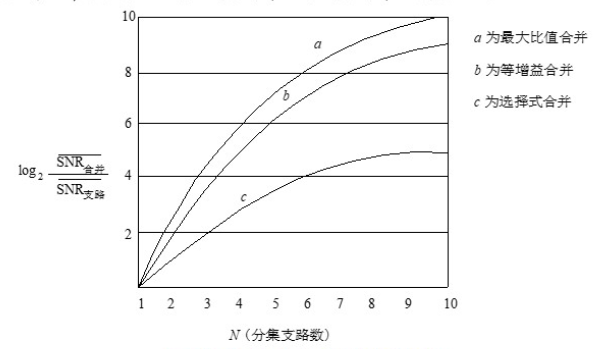
三种分集合并的性能如图所示。

可以看出，在这三种合并方式中，最大比值合并的性能最好，选择式合并的性能最差。比较增益表达式可以看出，当N较大时，等增益合并的合并增益接近于最大比值合并的合并增益。

$G_{M}=\frac{\overline{r_{m}}}{\overline{r_{0}}}=\sum_{k=1}^{N} \frac{1}{k} \\ 等增益合并： G_{M}=\frac{\overline{r_{M}}}{\bar{r}}=1+(N-1) \frac{\pi}{4} \\ 最大比合并: G_{M}=\frac{\overline{r_{M}}}{\bar{r}}=N$

Alamouti空时分组码(STBC)简介

Alamouti在1998年提出了一种采用两根发射天线的简单发射分集技术。Tarokh 等人在此基础上将其推厂到多根天线情况，并正式提出了STBC的概念。STBC的实质是一种空域和时域相结合的正交分组编码，利用正交设计的原理来分配多个发射天线的发射信号。由于STBC可以使接收机解码后获得完美的分集增益，且解码复杂度相对较低，因此，STBC在实际应用中是一类非常重要的空时编解码技术。

Alamouti方案是为发射天线数为 2 的系统提供完全发射分集增益的第一种空时分组码。

下图为Alamouti编码器原理图。

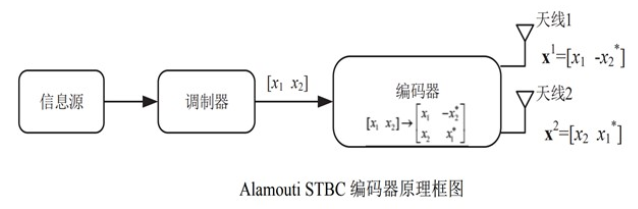
假设在Alamouti STBC方案中采用M进制调制。

首先将总的信息比特进行调制，得到调制符号;然后将调制符号分成两部分;最后根据Alamouti编码矩阵将两部分调制符号映射到两根发射天线上，其编码矩阵可以表示为

$[\begin{array}{cc} x_{1} & -x_{2}^{*} \\ x_{2} & x_{1}^{*} \end{array}]$

，其中 (·)*表示复共轭。

发射端通过两根发射天线在两个连续发射周期里发射调制符号。在第一个发射周期中, 天线 1 发射调制符号 $\boldsymbol{x}_{\mathbf{1}}$ , 天线 2 发射调制符号 $x_{2}$ ; 在第二个发射周期中, 天线 1 发射 $x_{2}^{*}$ , 天线 2 发射 $x_{1}^{*}$ 。可以看出, 第二个发射周期发射的调制符号和第一个发射周期的调制符号是相关的, 可以简单的认为第二个发射周期发射的调制符号是第一个发射周期发射的调制符号的副本。

在 Alamouti 方案中, 分别令

$\boldsymbol{X}^{\mathbf{1}}=[\begin{array}{ll} x_{1} & -x_{2}^{*} \end{array}] \text { 和 } \boldsymbol{X}^{2}=[\begin{array}{ll} x_{2} & x_{1}^{*} \end{array}]$

表示天线 1 和天线 2 的发射序列, 很显然 , 两根发射天线的发射序列是正交的, 即

$\boldsymbol{X}^{\mathbf{1}} \cdot(\mathbf{X}^{\mathbf{2}})^{*}=x_{1} x_{2}^{*}-x_{2}^{*} x_{1}=0$

此外, Alamouti 编码矩阵 $ \mathbf{X}$ 具有如下特性:

$\cdot X^{H}=[\begin{array}{cc} |x_{1}|^{2}+|x_{2}|^{2} & 0 \\ 0 & |x_{1}|^{2}+|x_{2}|^{2} \end{array}]$

其中 $(\cdot)^{\mathrm{H}}$ 表示矩阵的共轭转置。

下图为Alamouti的仿真结果。

其中MRRC表示最大比合并。Alamouti方案的检测采用ML，以最小欧式距离为测度。

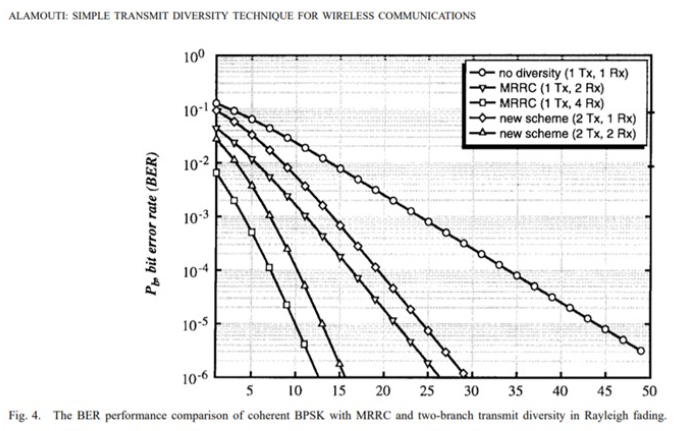
Alamouti空时分组码利用了空间分集和时间分集，发射天线数n=2，若接收天线数为m，则它的分集增益为2m。

优缺点:

结构简单，译码复杂度是线性的;
能够实现完全分集;
没有编码增益。

下图所示的分集是 (A)

A. 空间分集

B. 时间分集

C. 多径分集

D. 频率分集

参考文献：

Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
周炯槃. 通信原理（第3版）[M]. 北京：北京邮电大学出版社, 2008.
樊昌信, 曹丽娜. 通信原理（第7版） [M]. 北京：国防工业出版社, 2012.