目录
一. 关于堆排序
1. 堆的定义
二. 堆排序的实现
1. 堆排序的思路
2. 堆排序的问题分析
3. 堆排序的具体实施
4. 效率分析
三. 堆排序的代码实现
1. 堆排序
2. 调整堆(核心代码)
四. 代码展示
五. 数据测试
六. 总结
一. 关于堆排序
1. 堆的定义
n个关键字序列L[1...n]称为堆,当且仅当该序列满足:
①L(i)≥L(2i)且L(i)≥L(2i+1)或
②L(i)≤L(2i)且L(i)≤L(2i+1)————————(1≤i≤n/2)
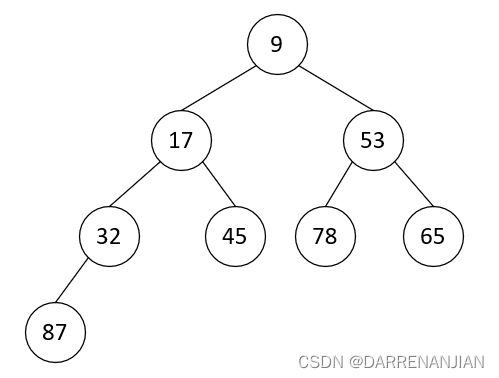
首先堆是一个完全二叉树(这是我们后面进行堆排序的前提条件),满足条件①的堆称为大根堆,大根堆的最大元素存放在根节点,且其任意一个非根节点的值小于或等于其双亲节点值。满足条件②的堆称为小根堆,小根堆的最小元素存放在根节点,且其任意一个非根节点的值大于或等于其双亲节点值,小根堆的定义恰好相反,根节点是最小元素。如下图所示大根堆,小根堆。

二. 堆排序的实现
1. 堆排序的思路
使用堆的元素下沉思想,即我先根据给定的数组序列构造一个堆,我每一次取根节点,并且将根节点删除(插入到最后一个位置),再对去掉根节点的数字序列构造一个堆;重复上述步骤即可得到最终的排序结果,除此之外这里没有递归调用,且使用的空间是常数,故在给定空间进行原地排序。具体步骤如下:
a、给定任意待排序的数组可以看作是是一颗完全二叉树(顺序存储完全二叉树的性质)。
b、然后将此二叉树转换为一个大顶堆。
c、最后依次将大顶堆的最大元素放在指定位置(去掉最大元素后,堆最后一个元素坐标的下一个坐标)。
2. 堆排序的问题分析
上面的思路写的其实很简单,a和c都很好理解,
现在我们的问题是:①最关键的b部,我们应该怎么样从无到有根据数字序列建立一个堆呢?②我们首次建立完成堆,并且再删除了根节点元素之后就破坏了原来的堆,我们又该如何重新建立堆呢?接下来我将叙述具体的实施过程。
3. 堆排序的具体实施
首先对于第一个问题:堆排序怎么样构建一个初始(大根)堆?
n个节点的完全二叉树,最后一个节点是第n/2个节点的孩子(完全二叉树的性质)。那么我们就从这个节点开始,对第n/2个节点为根的子树筛选(对于大根堆,若子树根节点的关键字小于左右还在中的关键字较大者,则交换根节点和左右孩子中的较大者),使以n/2节点为根的子树成为一个大根堆。接着我们继续向前一次对n/2-1——1为根的子树进行建堆,看每一个根节点是否都大于左右孩子中的较大者,若大于则不操作,若不大于则交换根节点和左右孩子中的较大者,并且注意,这里交换之后由于是在完全二叉树的上层,很有可能会破坏下层我们已经建立好的子树的大根堆,所以,我们还要对这个根节点进行筛查,若这个根节点仍然小于调整后的左右孩子节点的值,那么我们继续调整这个根节点,直到他满足大根堆的定义为止。最后我们反复利用上面的调整关系,使n/2号节点——1号节点的每一个节点都满足大根堆条件,故此建立初始堆完成。
接着我们考虑第二个问题:删除了根节点元素之后就破坏了原来的堆,我们又该如何重新建立(大根)堆?
其实对于这个问题,我们上面已经有了解答,由于是将排好序的大根堆的根节点和最后一个节点互换位置,那么我们可以得到只有根节点一个节点破坏了大根堆,那么我们只需调整根节点的位置即可,不需要再从n-1号节点一直筛选到1号节点了。根节点和它的第一个左右孩子节点比较,是否大于等于左右孩子中的较大者;若不满足则将根节点和左右孩子中的最大者交换位置,再判断这个时候根节点的位置是否满足大根堆,即是否大于等于左右孩子中的较大者;若大于等于则调整结束;若不满足则继续调整这个根节点的位置直到满足条件为止。接着我们又得到了一个排好序的大根堆,继续讲根节点和倒数第二个节点互换位置继续上层循环,直到序列只有一个节点为止。
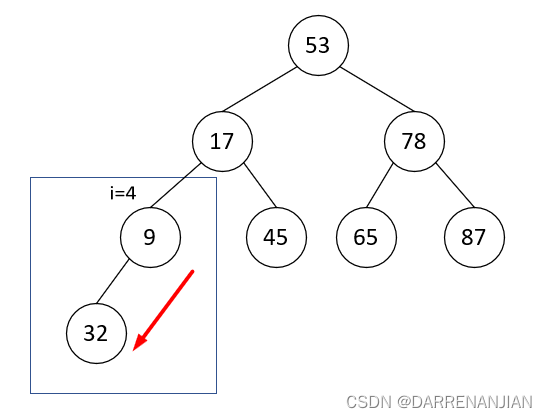
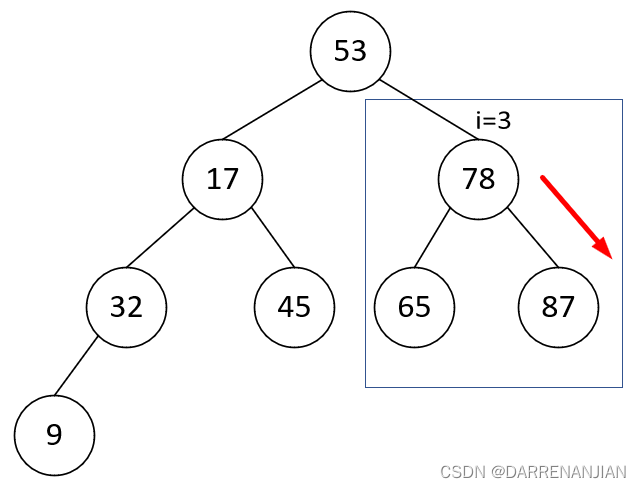
为了方便理解,下图是堆排序(大根堆)的过程:
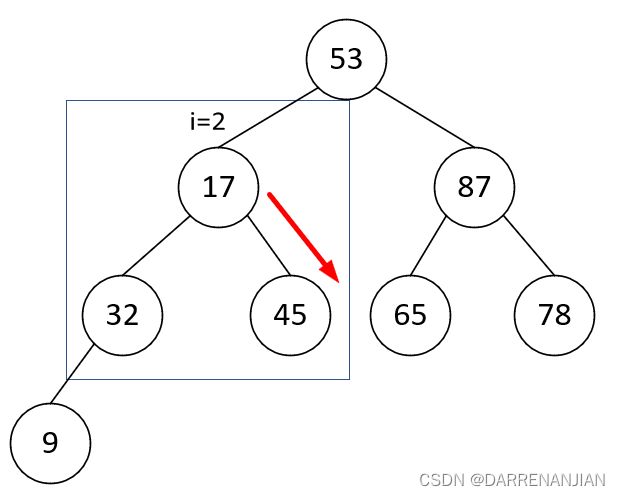
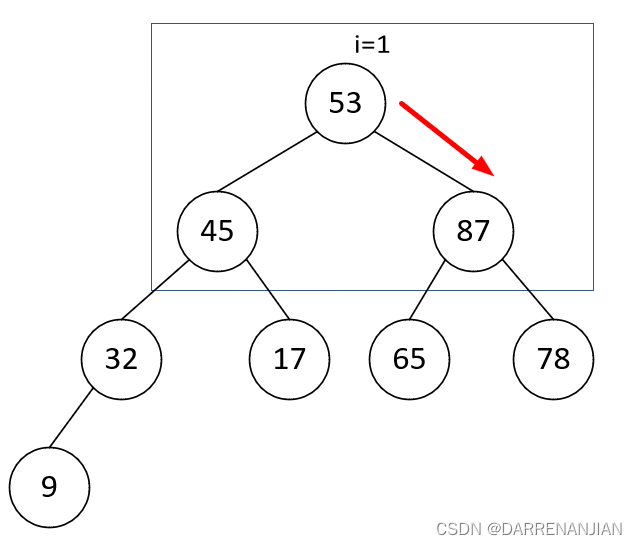
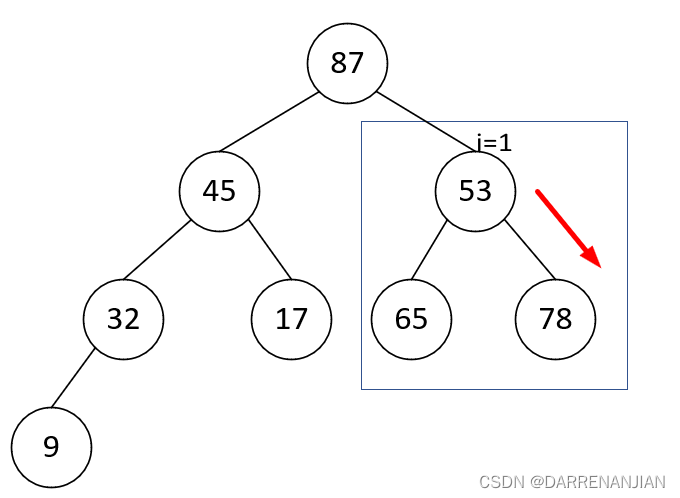
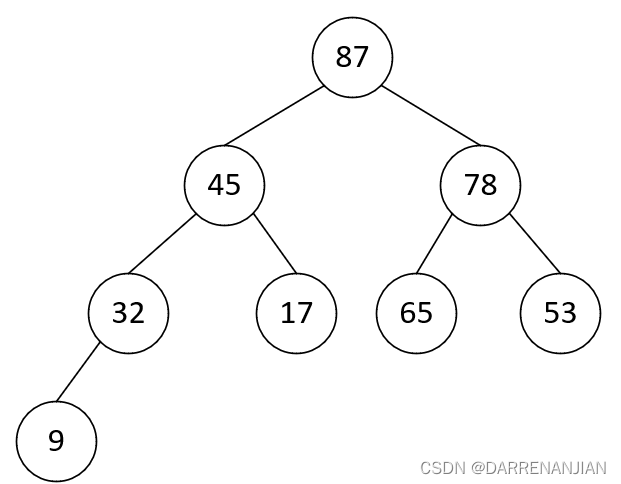
4. 效率分析
空间效率:仅使用了常数个辅助单元,空间复杂度为O(1)。
时间效率:建堆时间O(n),之后又n-1次向下调整操作,每次调整的时间复杂度为O(h),,故在最好,最坏和平均情况下,堆排序的时间复杂度为
稳定性:进行筛选时,有可能把后面相同 关键字的元素调整到前面,故是一种不稳定的算法。
三. 堆排序的代码实现
1. 堆排序
堆排序的总函数,非核心代码,相当于一个框架。
step1:给定调整大根堆函数;
step2:交换根节点和最后一个节点之后,破坏了大根堆,我们只需调整交换之后的根节点,使数字序列再次变为大根堆,继续step2的循环,直到最后一个节点结束。
/**
*********************
* Heap sort. Maybe the most difficult sorting algorithm.
*********************
*/
public void heapSort() {
DataNode tempNode;
// Step 1. Construct the initial heap.
for (int i = length / 2 - 1; i >= 0; i--) {
adjustHeap(i, length);
} // Of for i
System.out.println("The initial heap: " + this + "\r\n");
// Step 2. Swap and reconstruct.
for (int i = length - 1; i > 0; i--) {
tempNode = data[0];
data[0] = data[i];
data[i] = tempNode;
adjustHeap(0, i);
System.out.println("Round " + (length - i) + ": " + this);
} // Of for i
}// Of heapSort2. 调整堆(核心代码)
这部分代码就是堆排序的核心,函数名adjustHeap,传入两个参数,第一个参数paraStart是从哪个节点开始调整完全二叉树的子树为大根堆的节点位置,第二个参数paraLength是控制完全二叉树跳调整的范围(例如我再交换完根节点和最后一个节点之后,paraLength需要减1(因为最后一个节点相当于被删除))。
tempNode变量记录从哪个节点开始调整完全二叉树的子树为大根堆的节点数据
tempParent变量记录从哪个节点开始调整完全二叉树的子树为大根堆的节点位置
tempKey变量记录从哪个节点开始调整完全二叉树的子树为大根堆的节点标签
tempChild作为paraStart节点的左右孩子啊中标签最大的那个孩子节点的位置信息。接着进行判断,若父母节点的标签tempKey < 孩子节点的标签data[tempChild].key(不满足大根堆条件),则交换父母节点和孩子节点中的较大值;同时进行判断交换完之后的tempParent节点是否在新的位置满足大根堆,若满足结束循环,这个节点调整完完毕;若不满足,继续上述操作直到完成为止。最后我们得到了节点paraStart的最终位置信息。
综上所述其实问题的关键我觉得是理解paraStart和paraLength参数是表示什么,adjustHeap函数是将paraStart节点值一直向下调整到满足大根堆为止(其他节点一只耳没动(除了paraStart的孩子节点,因为可能要互换位置,其他子树一直没有发生位置变化)),所以这里我们只调整节点paraStart的位置信息,paraLength控制数字序列的长度。
/**
*********************
* Adjust the heap.
*
* @param paraStart The start of the index.
* @param paraLength The length of the adjusted sequence.
*********************
*/
public void adjustHeap(int paraStart, int paraLength) {
DataNode tempNode = data[paraStart];
int tempParent = paraStart;
int tempKey = data[paraStart].key;
for (int tempChild = paraStart * 2 + 1; tempChild < paraLength; tempChild = tempChild * 2 + 1) {
// The right child is bigger.
if (tempChild + 1 < paraLength) {
if (data[tempChild].key < data[tempChild + 1].key) {
tempChild++;
} // Of if
} // Of if
System.out.println("The parent position is " + tempParent + " and the child is " + tempChild);
if (tempKey < data[tempChild].key) {
// The child is bigger.
data[tempParent] = data[tempChild];
System.out.println("Move " + data[tempChild].key + " to position " + tempParent);
tempParent = tempChild;
} else {
break;
} // Of if
} // Of for tempChild
data[tempParent] = tempNode;
System.out.println("Adjust " + paraStart + " to " + paraLength + ": " + this);
}// Of adjustHeap
四. 代码展示
主类:
package Day_48;
import Day_41.DataArray;
public class demo1 {
/**
*********************
* The entrance of the program.
*
* @param args Not used now.
*********************
*/
public static void main(String args[]) {
// System.out.println("\r\n-------sequentialSearchTest-------");
int []paraKeyArray;
paraKeyArray=new int[]{11,2,3};
String[] paraContentArray = new String[]{"121","21","324"};
// System.out.println(paraKeyArray.length);
DataArray test=new DataArray(paraKeyArray,paraContentArray);
// test.insertionSort();
// System.out.println("Result\r\n" + test);
test.heapSortTest();
}// Of main
}调用类(这个类太长了,我只保留了这一节的代码)
/**
*********************
* Heap sort. Maybe the most difficult sorting algorithm.
*********************
*/
public void heapSort() {
DataNode tempNode;
// Step 1. Construct the initial heap.
for (int i = length / 2 - 1; i >= 0; i--) {
adjustHeap(i, length);
} // Of for i
System.out.println("The initial heap: " + this + "\r\n");
// Step 2. Swap and reconstruct.
for (int i = length - 1; i > 0; i--) {
tempNode = data[0];
data[0] = data[i];
data[i] = tempNode;
adjustHeap(0, i);
System.out.println("Round " + (length - i) + ": " + this);
} // Of for i
}// Of heapSort
/**
*********************
* Adjust the heap.
*
* @param paraStart The start of the index.
* @param paraLength The length of the adjusted sequence.
*********************
*/
public void adjustHeap(int paraStart, int paraLength) {
DataNode tempNode = data[paraStart];
int tempParent = paraStart;
int tempKey = data[paraStart].key;
for (int tempChild = paraStart * 2 + 1; tempChild < paraLength; tempChild = tempChild * 2 + 1) {
// The right child is bigger.
if (tempChild + 1 < paraLength) {
if (data[tempChild].key < data[tempChild + 1].key) {
tempChild++;
} // Of if
} // Of if
System.out.println("The parent position is " + tempParent + " and the child is " + tempChild);
if (tempKey < data[tempChild].key) {
// The child is bigger.
data[tempParent] = data[tempChild];
System.out.println("Move " + data[tempChild].key + " to position " + tempParent);
tempParent = tempChild;
} else {
break;
} // Of if
} // Of for tempChild
data[tempParent] = tempNode;
System.out.println("Adjust " + paraStart + " to " + paraLength + ": " + this);
}// Of adjustHeap
/**
*********************
* Test the method.
*********************
*/
public static void heapSortTest() {
int[] tempUnsortedKeys = { 5, 3, 6, 10, 7, 1, 9 };
String[] tempContents = { "if", "then", "else", "switch", "case", "for", "while" };
DataArray tempDataArray = new DataArray(tempUnsortedKeys, tempContents);
System.out.println(tempDataArray);
tempDataArray.heapSort();
System.out.println("Result\r\n" + tempDataArray);
}// Of heapSortTest五. 数据测试
运行数据

六. 总结
这一节的堆排序可以算的上是数据结构排序算法里面比较难的部分了,这里有三个问题是关键①如何构建初始(大根)堆,②由于交换排好序的根节点和最后一个节点,破坏了(大根)堆,我们该如何修复他?③再构建大根堆的过程中(由于是从下往上构建大根堆)在上层调整节点位置时,难免会破坏下层的大根堆子树,我们又该做什么样的解决办法。
其实对于这个算法我更想形象的把这个算法比作一个系统,每次根据这个系统的运行结果调整参数(节点值),然后不断迭代,最终得到我们想要的答案。


![[golang 微服务] 5. 微服务服务发现介绍,安装以及consul的使用,Consul集群](https://img-blog.csdnimg.cn/img_convert/b9241e5ff389455e8b947a59d0a1a1f4.png)