算法笔记(六)

---

前言

检索算法又叫查找算法，可以分为排序检索和非排序检索两大类。排序的数据为高校检索提供了基础。当然非排序也存在，只不过效率很低。本章一起来学习几种检索算法。

---

一、线性查找

1.什么是线性查找

线性查找(Linear Search)又叫作顺序查找，是最简单的一种查找方法。

2.需求规则

1. 实现思路：从第一个元素开始依次查找比较，若查找成功，则返回找到元素的下标或确认信息；若查找失败，则返回查找失败信息。
2. 线性查找既可以从左边开始，也可以从右边开始。
3. 线性查找可以用于排序数列的查找，也可以用于无序数列的查找。

3.人工图示演示

图所示为线性查找过程，从左到右依次比较查找。查找值key=5时，
返回没有找到;

4.代码实现

def linearfind(arr, key):
   n = len(arr)
   i = 0
   while i < n:
       if arr[i] == key:
           return i
       i += 1
   return -1


s1 = [66, 79, 65, 25, 54, 99, 101, 100]
key = 6
r = linearfind(s1, key)
if r != -1:
   print(f'{key}被找到，在第{r}位上')
else:
   print(f"{key}没有被找到")

运行结果

二、二分查找

1.什么是二分查找

二分查找( Binary Search)算法采用折半查找思路，实现对有序元素的快速查找。

2.需求规则

1. 前提条件是数据已经排序。
2. 在数列中取中间下标值为mid的元素E,然后将元素E与查找值key进行比较，如果相等即查找成功，并返回其下标mid;如果E>key,则在左边范围内继续取新的mid下标值元素，判断两者大小:如果E<key,则在右边范围内继续取新的mid下标值元素，判断两者大小。上述过程迭代进行，直到查找范围缩小为一个元素，查找结束并返回查找结果。

3.人工图示演示

图示为二分查找过程，列表共有n=11个元素。
第一次，取中间值mi-1/2-5,其左边范围为left=0、 右边范围为right=10， 比较结果
key-55在右半边的范围内。
第二次，取新的中间值mid-s/2 2,其左边范围为lef-5+1、右边范围为igh=10,比较结果
key-55在右半边的范围内。
第三次，取新的中间值m-2/2=I,其左边范围为let-6+2+1.右边范围为rgh=l0,比较结
果在下标10处找到55。

4.代码实现

	def binaryrearch(arr, key):
    left = 0
    right = len(arr)
    while left <= right:
        mid = (right - left) // 2     # 二分法中间位置
        if arr[left + mid] < key:     # key 在右半范围
            left = left + mid + 1
        elif arr[left + mid] > key:   # 左半范围
            left = left + mid - 1
        else:
            return left + mid         # 找到下标 
    return -1


s1 = [0, 10, 20, 30, 40, 50, 60, 70, 80]
print(f"查找列表{s1}")
key = 40
r = binaryrearch(s1, key)
if r == -1:
    print(f"未找到{key}元素")
else:
    print(f"在列表第{r}找到{key}元素")

运行结果

三.插值查找

1.什么是插值查找

插值查找(Interpolation Search) 是基于有序数列的元素查找，在采纳二分查找算法的思路基础上进行了改进。在最小值、最大值范围内，用公式确定中间分割比较点mid

2.需求规则

1. 图式的基本思路是用最大值与最小值之差和中间值与最小值之差的比值乘以最大值和最小值下标范围差，以确定查找中间范围下标值mid.注意最大值和最小值下标范围就是要查找的范围，而后确定范围的中间值，以分割思路进行比较。
2. 通过比较arr[mid]与key的大小，确定结果是相等、小于还是大于，然后决定是否再缩小分割，直到找到元素值或查找结束。

3.人工图示演示

图所示为插值查找过程，left=0, right=8， mid=8*(50-0)/50=8。

4.代码实现

def valuyesearch(arr, key):
    left = 0
    right = len(arr) - 1
    while left < right:
        mid = left + int((right - left) * (key - arr[left]) / (arr[right] - arr[left]))
        if key < arr[mid]:
            right = mid - 1
        elif key > arr[mid]:
            left = mid + 1
        else:
            return mid
    return -1


s1 = [0, 10, 20, 30, 40, 50, 60, 70, 80]
print(f"查找列表{s1}")
key = 60
r = valuyesearch(s1, key)
if r == -1:
    print(f"未找到{key}元素")
else:
    print(f"在列表第{r}找到{key}元素")

运行结果

四.斐波那契查找

1.什么是斐波那契查找

斐波那契数列(Fibonacci Sequence)又称黄金分割数列，指的是这样一个数列: 1、 1、 2、3、5、8、13、21、······ 在数学上斐波那契被递归方法如下定义: F(1)=1， F(2)=1, F(n)=F(n 1)+F(n-2) (n≥2)。该数列越往后，相邻的两个数的比值越趋向于黄金比例值(0.618)。
斐波那契查找就是在二分查找的基础上根据斐波那契数列对数据进行分割的。

2.需求规则

1. 提供有序排列的列表对象s=[0,3,5,7,10,30,50,70,80,100]， 其个数n=10。
2. 利用斐波那契数列1、1、2、3、5、8、13、21、.，作为下标来分割列表元素范围。
3. 为了满足斐波那契数列中下标范围要求，提供的列表如果不满足要求，则缺省的数字用列表最后一个元素重复填补，如这里的n=10,但是10后最靠近的斐波那契数是13， 其缺失的下标为10、11 和12的元素都用100来填补。
4. 比较查找的key值在斐波那契数列的哪个范围内，找到返回，找不到给予提示。

3.人工图示演示

图示为斐波那契查找过程。
第一步，判断s数列的长度是否满足n=13，如果不满足，则用最后一个元素100 补充3个 100 (13-n=3)。
第二步，中间下标值mid取最右边值13-1 (斐波那契最后一个数是13)， 因为70<100，说明70值范围在左边。
第三步，中间下标值mid取8-1 (斐波那契倒数第2个数是8)，key=70, 找到元素。

4.代码实现

def fibonaccisearch(arr,key):
    n = len(arr)
    i = 1
    F = [1,1,]
    while F[i] <= n:
        F.append(F[i-1]+F[i])
        i += 1
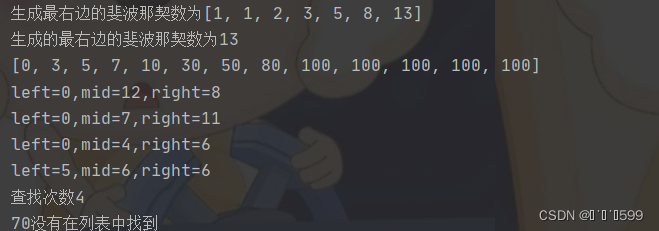
    print(f'生成最右边的斐波那契数为{F}')
    left = 0
    right = n - 1
    f = F[i]
    print(f'生成的最右边的斐波那契数为{f}')
    i = 0
    while i< f - n:
        arr.append(arr[right])
        i += 1
    print(arr)
    k = len(F)
    t = 0
    while left <= right:
        t += 1
        if k < 2:
            mid = left
        else:
            mid = left + F[k-1] - 1
        print(f"left={left},mid={mid},right={right}")
        if key < arr[mid]:
            right = mid - 1
            k -= 1
        elif key > arr[mid]:
            left = mid + 1
            k -= 2
        else:
            print(f"查找次数{t}")
            if mid <= right:
                return mid
            else:
                return right
    print(f"查找次数{t}")
    return False
key = 70
s1 = [0,3,5,7,10,30,50,80,100]
r = fibonaccisearch(s1,key)
if r == False:
    print(f"{key}没有在列表中找到")
else:
    print(f"查找{key}在列表里的下标{r}")

运行结果

五.分块查找

1.什么是分块查找

分块查找，又叫索引顺序查找，是顺序查找的一种改进方法。

2.需求规则

1. 输入列表元素分块之间的值顺序排序
2. 实现思路是把数列元素分为m个分块，m<=n，其中n为列表长度。建立每个分块最大值的索引表，通过查找值key与索引表值范围的比较，确定其查找范围或返回没有该值；然后，进一步根据查找范围确定查找值所在分块，用线性查找方法查找所在分块里的查找内容，得出查找结果。

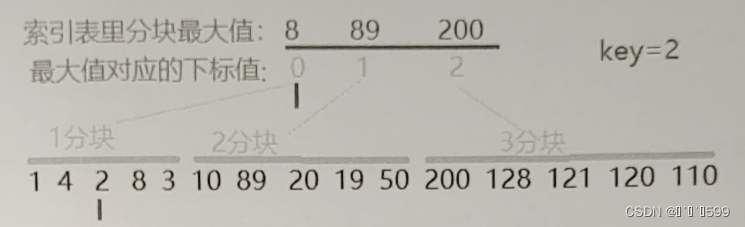
3.人工图示

1. 图示为分块查找过程。查找的前提条件是分块之间值是顺序的，例如，1分块内的元素都小于2分块的，2里面的元素均小于3方块里的，但允许每个方块里的元素无序。
2. 第一步，先在索引表里按顺序存储每个分块的最大值，这意味着第一个元素8的下表0刚好对应分块1，第二个元素89的下标1对应分块2，第三个元素200的下标2对应分块3.
3. 第二部，通过关键值key=2与索引表值比较，得出元素2在范围8内，通过元素8的下标0，确定元素2属于1分块范围
4. 第三步，在1分块子列表里用线性查找法找元素2，找到2并返回其列表下标值2，查找结束。

4.代码实现

def linearfind(arr, key):
    n = len(arr)
    i = 0
    while i < n:
        if arr[i] == key:
            return i
        i += 1
    return -1


def blocksearch(arr, key, index, n):
    b_max = -1
    j = 0
    for i in index:
        j += 1
        if key <= i:
            b_max = i
            break
    if b_max == -1:
        return -1
    print(f"块内最大值为{b_max}")
    r = linearfind(arr[(j - 1) * n:(j * n - 1)], key)
    print(f"线性查找结果：{r}")
    if r == -1:
        return -1
    else:
        return (j - 1) * n + r


s1 = [1, 4, 2, 8, 3, 10, 89, 20, 19, 50, 200, 128, 121, 120, 110]
index = [8, 89, 200]
key = 2
r = blocksearch(s1, key, index, 5)
if r == -1:
    print(f"{key}在列表里不存在")
else:
    print(f"{key}在列表里的下标为{r}")

运行结果

六.哈希查找

1.什么是哈希查找

哈希查找算法采用键值对存储数据的哈希表，通过哈希函数决定存储地址，并利用元素对应的地址直接在哈希表里进行1次访问即解决查找问题，时间复杂程度为O(1)，效率很高。

1.需求规则

1. 获取哈希表的长度n
2. 利用元素值%n取余，获得对应的地址(字典的键)；在地址发生冲突时，通过增1方式试探产生下一个地址
3. 建立字典存储键值（地址-元素）
4. 再利用元素值%n求余，在字典里通过地址，一次访问找到值或给出找不到值的提示

2.人工图示演示

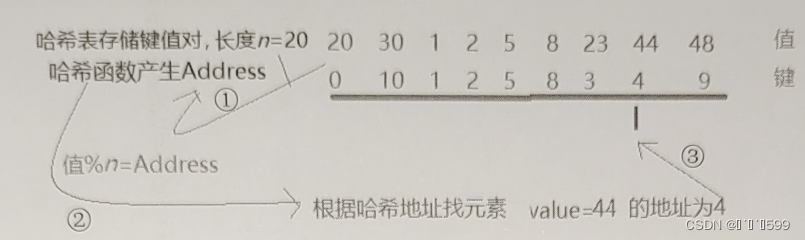
第一步，建立哈希表，哈希表的元素为键值对，在python语言里可以看作字典。键用于存放唯一性地址，值用于存放数据。
第二步，用哈希函数(hash()产生键（address）)，产生键的唯一要求是产生具有唯一地址的数值。产生键的算法有很多种，这里采用了除留余数法，公式为元素值%n，n为哈希表的长度；对于重复发生冲突的地址，采用试探下一个地址的方法解决（观察48产生的地址9）
第三步，查找元素时，也采用哈希函数算法先找到地址，然后在哈希表里1次找到对应的值（如果找不到，试探下一个地址，直到哈希表结束）。

4.代码实现

maxsize = 20
hashtable = {i: None for i in range(maxsize)}
print(f"哈希表大小为{len(hashtable)}")


def hash(value):
    address = value % maxsize
    if hashtable[address] == None:
        return address
    else:
        while address < maxsize:
            address += 1
            if hashtable[address] == None:
                return address
    return -1


def buildhashtable(values):
    for value in values:
        address = hash(value)
        print(f"建立的键值对({address},{value})")
        if address != -1:
            hashtable[address] = value
        else:
            print(f"数值{value}存放的哈希表地址不够")
    return hashtable


def findvalue(hasht, value):
    address = value % maxsize
    if hasht[address] == value:
        return True
    else:
        address += 1
        while address < maxsize:
            if hasht[address] == value:
                return True
            address += 1
    return False


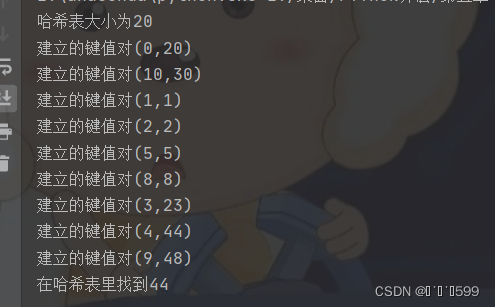
s1 = [20, 30, 1, 2, 5, 8, 23, 44, 48]
value = 44
if findvalue(buildhashtable(s1), value):
    print(f"在哈希表里找到{value}")
else:
    print(f"在哈希表里找不到{value}")

运行结果

七.回溯查找

1.什么是回溯查找

回溯算法(Backtracking Algorithm)是一个类 似枚举的搜索尝试过程，在尝试过程中寻找问题的解，当发现条件不满足要求时，回退寻找另外路径求解，反复迭代上述过程，直到找出满足要求的所有条件(即为一个解)，或者不存在解。
许多复杂的、规模较大的问题都可以使用回溯查找法求解，该算法有“通用解题方法”的美称。

2.需求规则

1. 建立回溯空间的数据结构(二维表或二维数组)。
2. 按照一定条件试探性地在空间搜索，成功继续往下搜索;不成功回退，选择另外一个方 向继续试探。
3. 直到所有的条件都满足，求得最优解;或得出不存在最优解。

3.人工图示演示

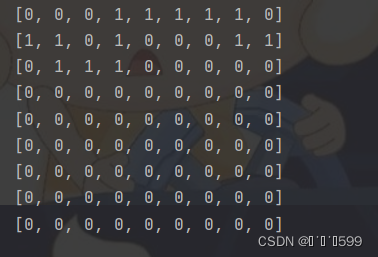
图示为走迷宫主要思路。左上角第一个矩阵中0代表墙，1代表道路。要求只能从第1列的任意一个口进入，最后一列任意一个口出去， 才算走出迷宫。图右上角是一.条能走通的迷宫路。

1. 规则1.理论上除了边角节点外，当前节点往下一步走，需要考虑的节点最多有四个(右、下、左、上)，图左下角显示箭头所指中间圈里的1代表可走节点，四周从右、下、左、上四个紧邻节点的值判断是从该节点出发，然后需要判断哪条路可以走。 显然，这个节点右边有一个1，可以往右走。
2. 规则二。当碰到断头路时，不能再走下去了，只能往回走，寻找下一个出路，这叫回溯过程。如图右下角圈里的1，上，右，下都是墙壁，无法继续往前走，于是通过record记录的前一步的1往回退，并在maze里把当前1设置为0，代表不能走。继续利用规则1寻找下一个可走的道路，直到走到最右列，只找到一条可通的路。

4.代码实现

def findnext(m, record, r, c):
    n = len(m)
    if (c + 1 < n):
        if record[r][c + 1] == 0:
            if m[r][c + 1] == 1:
                record[r][c + 1] = 1
                return r, c + 1
        else:
            b_r, b_c = r, c + 1
    if r + 1 < n:
        if record[r + 1][c] == 0:
            if m[r + 1][c] == 1:
                record[r + 1][c] = 1
                return r + 1, c
        else:
            b_r, b_c = r + 1, c
    if r - 1 >= 0:
        if record[r - 1][c] == 0:
            if m[r - 1][c] == 1:
                record[r - 1][c] = 1
                return r - 1, c
        else:
            b_r, b_c = r - 1, c
    if c - 1 >= 0:
        if record[r][c - 1] == 0:
            if m[r][c - 1] == 1:
                record[r][c - 1] = 1
                return r, c - 1
        else:
            b_r, b_c = r, c - 1
    m[r][c] = 0
    if r + 1 == n and m[r][0] == 0:
        print(r, c)
        b_r, b_c = r + 1, 0
    return b_r, b_c


def solution_maze(m, record):
    row, col = 0, 0
    n = len(m)
    i = 0
    while i < n:
        if m[i][0] == 1:
            row = i
            record[i][0] = 1
            break
        i += 1
    if i == n - 1:
        print("第一列无入门地方，终止执行")
    while i < n:
        if (row < n and row >= 0) and (col < n and col >= 0):
            if col == n - 1:
                for one in record:
                    print(one)
                return 1
            row, col = findnext(m, record, row, col)
            if col == 0:
                i += 1
                row = i
    return 0


if __name__ == '__main__':
    maze = [[0, 1, 0, 1, 1, 1, 1, 1, 0],
            [1, 1, 0, 1, 0, 1, 0, 1, 1],
            [0, 1, 1, 1, 0, 1, 0, 0, 0],
            [0, 1, 0, 0, 1, 1, 0, 0, 0],
            [0, 1, 1, 1, 1, 0, 1, 1, 1],
            [0, 0, 1, 0, 0, 0, 1, 0, 1],
            [1, 1, 1, 1, 1, 1, 1, 0, 1],
            [0, 1, 1, 0, 0, 0, 0, 0, 1],
            [1, 0, 1, 0, 0, 0, 0, 0, 1]]
    n = len(maze)
    recordpath = [([0]*n) for _ in range(n)]
    solution_maze(maze,recordpath)

运行结果

---

总结

有关检索算法就这些了，有哪块不懂得欢迎 点击这里加入直接问问题，一起探讨。