💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
2.1 算例1
2.2 算例2
2.3 算例3
2.4 算例4
2.5 算例5
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
文献来源:

时频(TFA)分析(TFA)方法是工业工程领域的重要工具。然而,局限于海森堡不确定性原理或意外交叉项,经典TFA方法经常产生模糊的TF表示,严重阻碍了其工程应用。如何为强时变信号生成集中TF表示是一项具有挑战性的任务。在本文中,我们提出了一种新的TFA方法来研究强时变信号的非平稳特征。该方法基于同步挤压变换,采用迭代重分配程序逐步集中模糊TF能量,同时保持信号重构能力。给出了离散算法的两种实现方式,表明所提方法计算负担有限,具有实时应用潜力。此外,我们引入了一种有效的算法来检测瞬时频率轨迹,可用于分解单分量模态。通过与一些先进方法的比较,利用数值和真实世界信号验证了所提方法的有效性。通过对比表明,所提方法在处理强时变信号和噪声信号方面具有较好的性能。
原文摘要:
Abstract:
Time-frequency (TF) analysis (TFA) method is an important tool in industrial engineering fields. However, restricted to Heisenberg uncertainty principle or unexpected cross terms, the classical TFA methods often generate blurry TF representation, which heavily hinder its engineering applications. How to generate the concentrated TF representation for a strongly time-varying signal is a challenging task. In this paper, we propose a new TFA method to study the nonstationary features of strongly time-varying signals. The proposed method is based on synchrosqueezing transform and employs an iterative reassignment procedure to concentrate the blurry TF energy in a stepwise manner, meanwhile retaining the signal reconstruction ability. Two implementations of the discrete algorithm are provided, which show that the proposed method has limited computational burden and has potential in real-time application. Moreover, we introduce an effective algorithm to detect the instantaneous frequency trajectory, which can be used to decompose monocomponent modes. Numerical and real-world signals are employed to validate the effectiveness of the proposed method by comparing with some advanced methods. By comparisons, it is shown that the proposed method has the better performance in addressing strongly time-varying signals and noisy signals.
时频(TF)分析(TFA)是分析时变信号的有效工具,在过去几十年中引起了相当大的关注[1],[2]。经典的线性方法,如短时傅里叶变换(STFT)和小波变换(WT),可以将一维(1-D)时间序列信号扩展到二维(2-D)TF平面。从TF平面,我们可以观察时变特征并进行信号分解。然而,受海森堡不确定性原理的限制,通过常规方法生成的TF表示通常模糊,并且无法为时变信号提供精确的TF描述。TFA方法的最新发展涉及设计高分辨率方法,同时保留恢复原始时间序列信号的能力[3]。因此,我们可以尽可能详细地确定时变特征,并实现多分量模态的分解。
📚2 运行结果
2.1 算例1


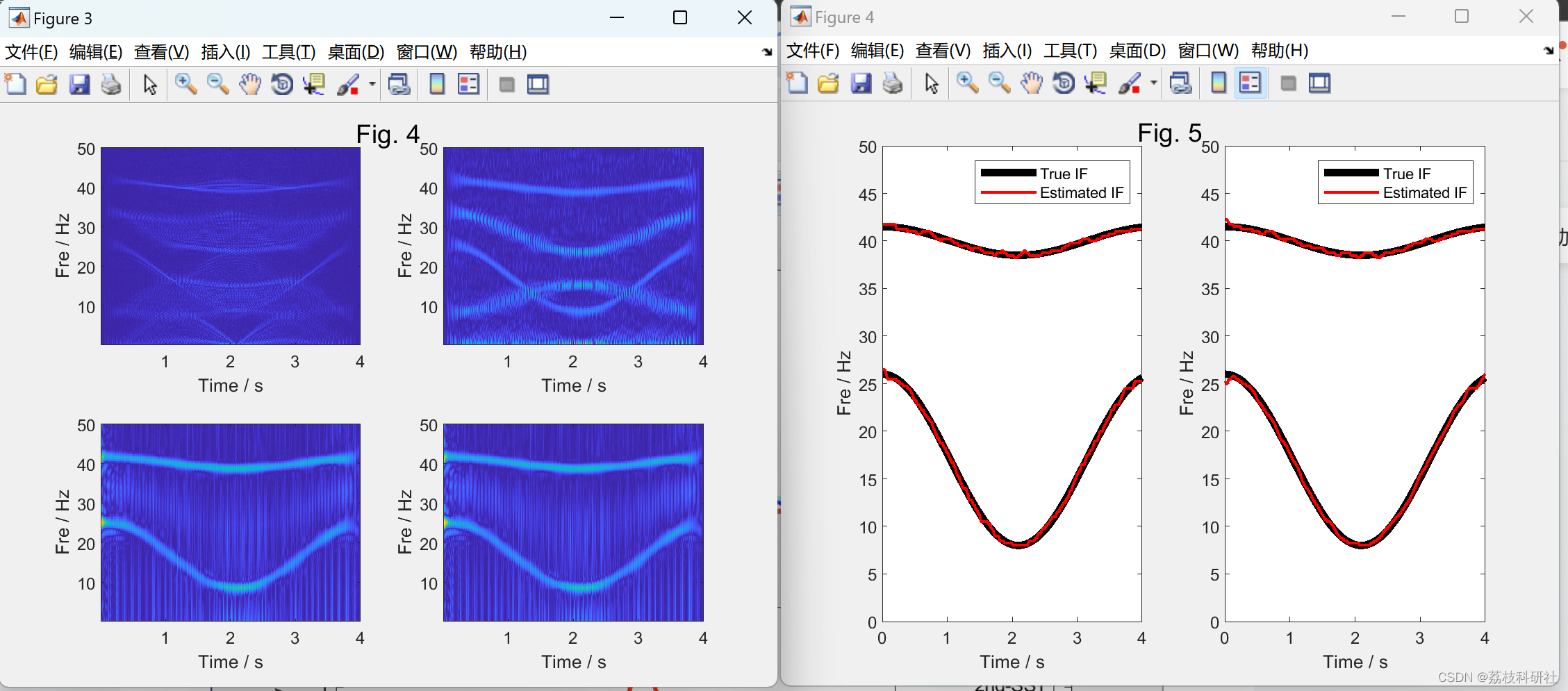
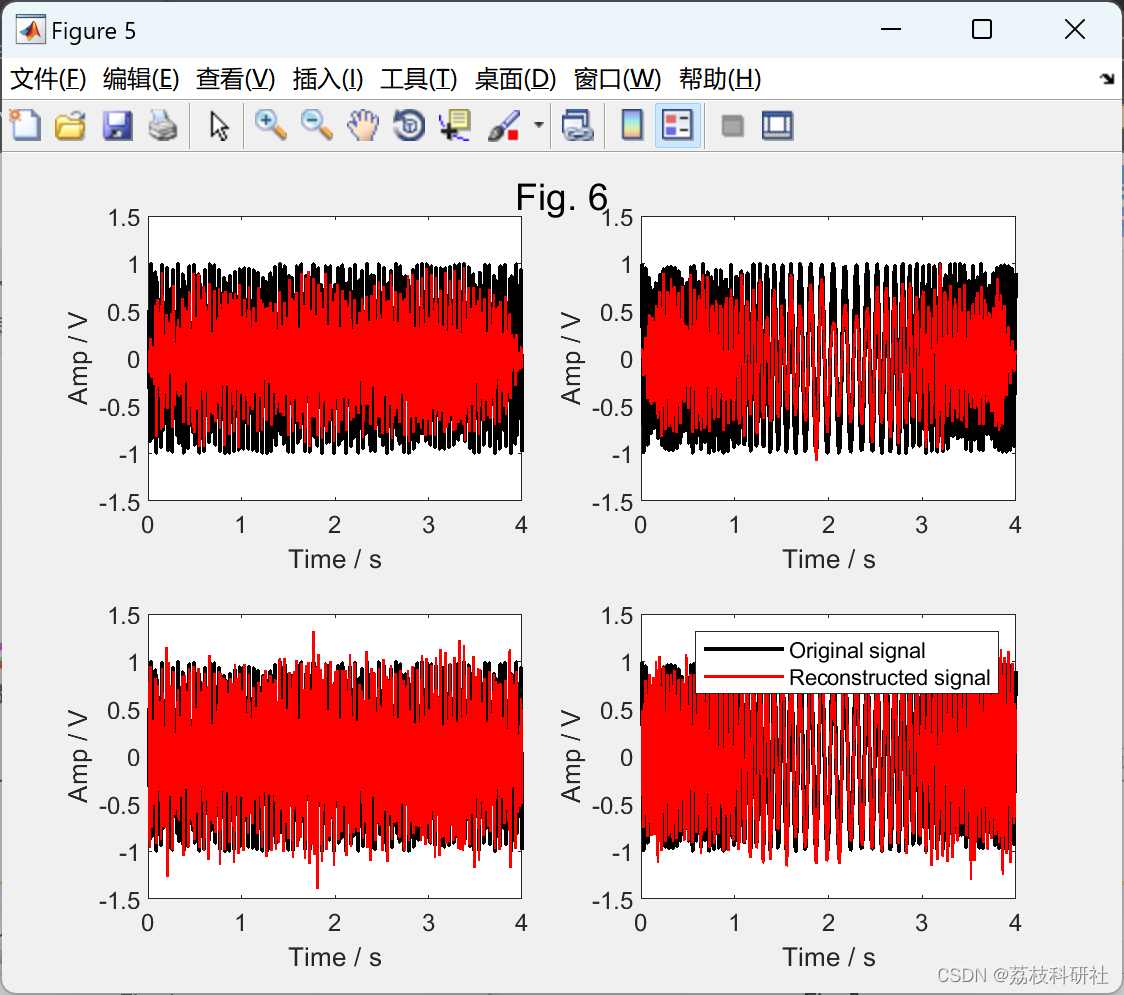
2.2 算例2

2.3 算例3

2.4 算例4

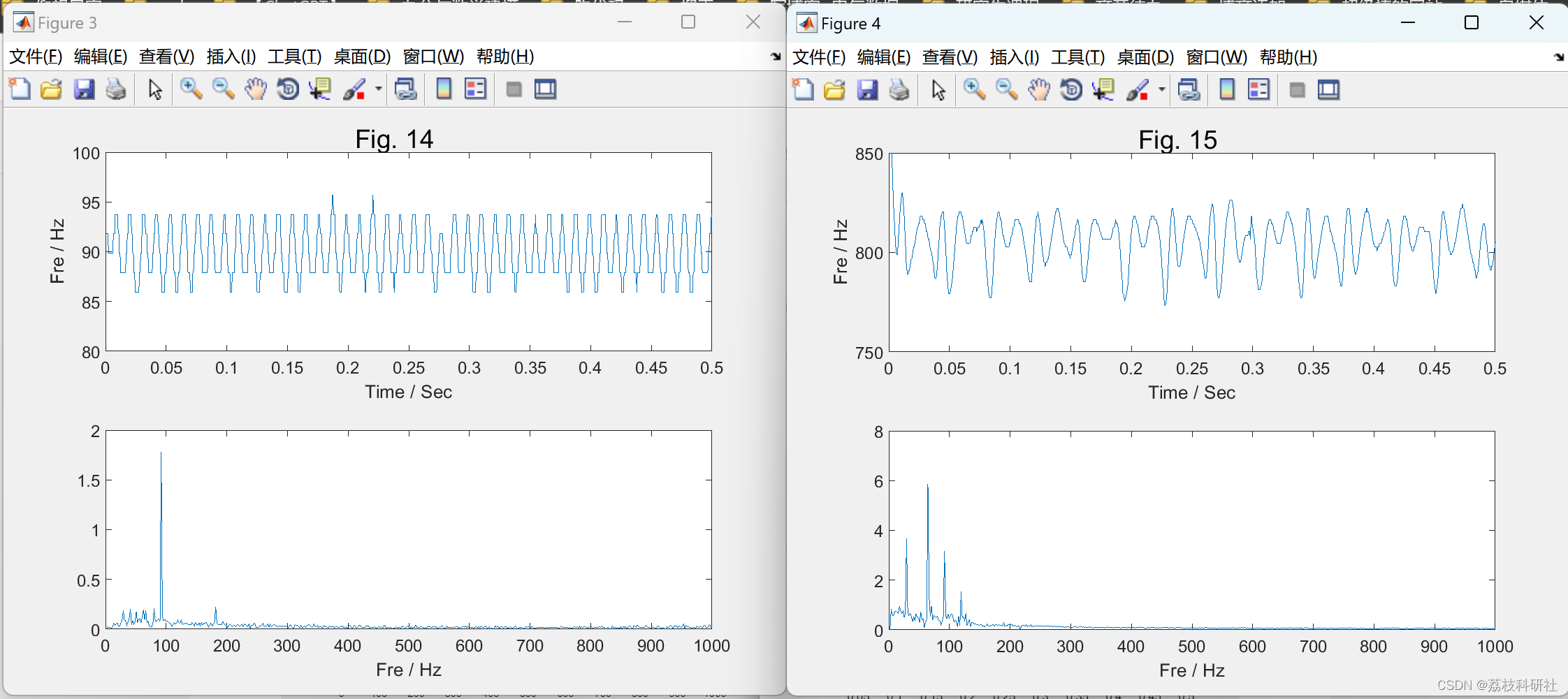

2.5 算例5



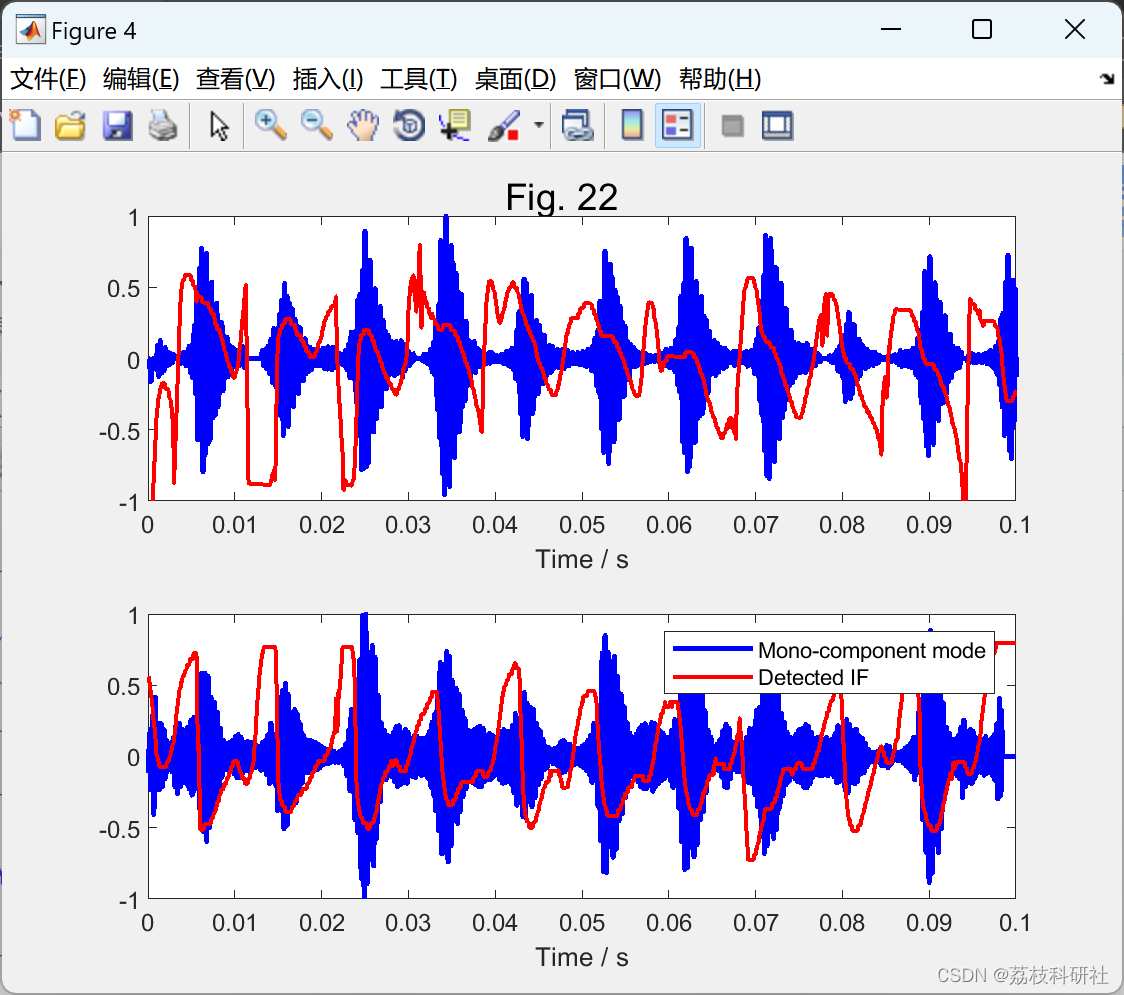
部分代码:
load('vib_data1.mat')
fs = 12000; N = 1200; % sampling frequency and points
time = (1:N)/fs; % time sequence
fre = (fs/2)/(N/2):(fs/2)/(N/2):(fs/2); % frequency sequence
data=data(1:N);
[MTs tfr]=MSST_Y_new(data,95,50);
gamma = 10^(-2);
sigma = 0.025;
[~,~,~,~,~,Ts1,Ts2,Ts3,Ts4] = sstn(data,gamma,sigma);
.................................................................
figure
suptitle('Fig. 19');
subplot(211)
plot(time,data);
ylabel('Amp / g');
xlabel('Time / s');
axis([0 0.1 -4 4]);
subplot(212)
ft=abs(fft(data))/600;
plot(fre,ft(1:end/2));
ylabel('Amp / g');
xlabel('Fre / Hz');
axis([0 6000 0 0.3]);
...........................................................................
x1=0.06; x2=0.065;
y1=2.6; y2=3.7;
dd=0.1;
figure
suptitle('Fig. 20');
subplot(511);
imagesc(time,fre/1000,abs(tfr));
%xlabel('Time / s');
ylabel('Fre / kHz');
axis xy;axis ([0 0.1 y1-dd y2+dd]);
rectangle('Position',[x1 y1 x2-x1 y2-y1],'EdgeColor','red','Linewidth',1);
axes('position',[0.92,0.805,0.07,0.15]);
imagesc(time,fre/1000,abs(tfr));
%xlabel('Time / s');
ylabel('Fre / kHz');
axis xy
axis off;
%set(ha,'xlim',[x1 x2],'ylim',[y1 y2]);
xlim([x1,x2]);ylim([y1,y2]);
subplot(512);
imagesc(time,fre/1000,abs(Ts1));
%xlabel('Time / s');
ylabel('Fre / kHz');
axis xy;axis ([0 0.1 y1-dd y2+dd]);
rectangle('Position',[x1 y1 x2-x1 y2-y1],'EdgeColor','red','Linewidth',1);
axes('position',[0.92,0.61,0.07,0.15]);
imagesc(time,fre/1000,abs(Ts1));
%xlabel('Time / s');
ylabel('Fre / kHz');
axis xy
axis off;
%set(ha,'xlim',[x1 x2],'ylim',[y1 y2]);
xlim([x1,x2]);ylim([y1,y2]);
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]G. Yu, Z. Wang and P. Zhao, "Multisynchrosqueezing Transform," in IEEE Transactions on Industrial Electronics, vol. 66, no. 7, pp. 5441-5455, July 2019, doi: 10.1109/TIE.2018.2868296.