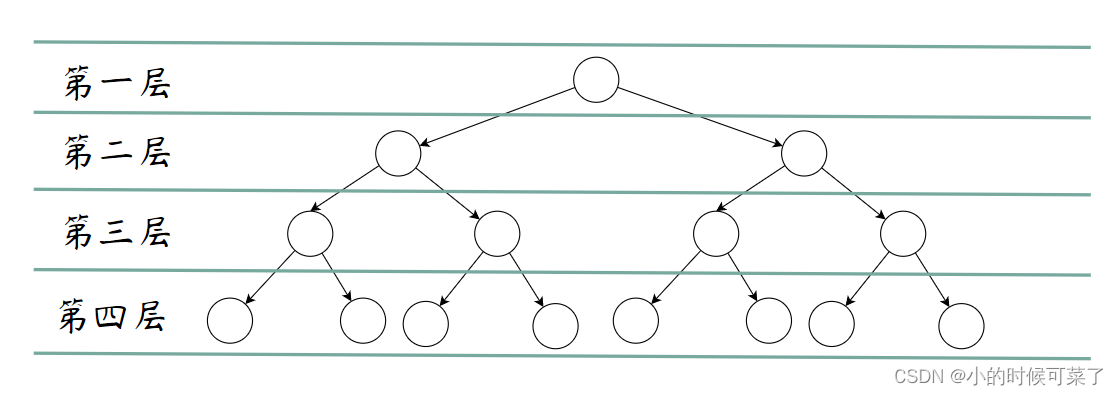
每层个数的通式
第一层: 2 0 第二层: 2 1 第三层: 2 2 第四层: 2 3 每层个数的通式 2 n − 1 个, n 为层数 \begin{aligned} 第一层:2^0 \\ 第二层:2^1 \\ 第三层:2^2 \\ 第四层:2^3 \\ \\ 每层个数的通式 \\ 2^{n-1} 个,n 为层数 \end{aligned} 第一层:20第二层:21第三层:22第四层:23每层个数的通式2n−1个,n为层数
总节点个数计算:
等比数列求和公式: a 1 ( 1 − q n ) 1 − q 总节点个数计算: 1 ( 1 − 2 2 ) 1 − 2 = 2 n − 1 \begin{aligned} 等比数列求和公式:\frac{a_1(1-q^n)}{1-q} \\ \\ 总节点个数计算:\\ \frac{1(1-2^2)}{1-2} \\ =2^n - 1 \end{aligned} 等比数列求和公式:1−qa1(1−qn)总节点个数计算:1−21(1−22)=2n−1
【总节点个数】与【最底层个数】的关系
总节点个数 2 n − 1 与每层个数 2 n − 1 之间的关系 2 n − 1 = 2 × 2 n − 1 − 1 即:总节点个数 = 2 × 最底层节点数 − 1 \begin{aligned} 总节点个数 ~ 2^n - 1 ~ 与 每层个数 ~ 2^{n-1} ~ 之间的关系 \\ 2^n - 1 = 2 \times 2^{n-1} -1 \\ 即:总节点个数 = 2 \times 最底层节点数 - 1 \end{aligned} 总节点个数 2n−1 与每层个数 2n−1 之间的关系2n−1=2×2n−1−1即:总节点个数=2×最底层节点数−1
为何左节点下表为 2i + 1
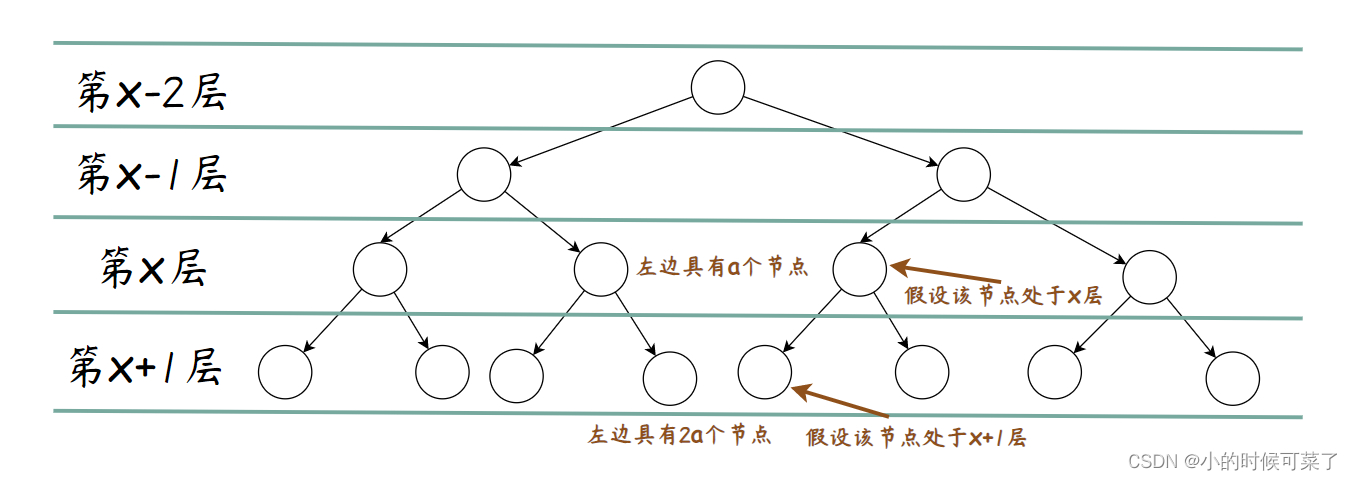
第 x 层,【假设节点】的下标
= 第
x
−
1
层
x - 1 层
x−1层的所有节点数 + a
=
(
2
x
−
1
−
1
)
+
a
(2^{x-1}-1) + a
(2x−1−1)+a
x-1 层总节点个数 + 假设节点左侧具有的节点数 a
同理可得 【左节点】的下标
=
(
2
x
−
1
)
+
2
a
(2^{x}-1) + 2a
(2x−1)+2a
x 层总节点个数 + 假设节点左侧具有的节点数 2a
【假设节点】的下标与【左节点】的下标 之间的关系
2
×
【假设节点】的下标
=
2
×
[
(
2
x
−
1
−
1
)
+
a
]
=
2
x
−
2
+
2
a
∴
【左节点】的下标
=
(
2
x
−
1
)
+
2
a
=
2
×
【假设节点】的下标
+
1
\begin{aligned} 2 \times 【假设节点】的下标\\ = 2\times [(2^{x-1}-1) + a] \\ = 2^{x} - 2+ 2a \\ \\ \therefore 【左节点】的下标= (2^{x}-1) + 2a \\ = 2 \times 【假设节点】的下标+ 1 \end{aligned}
2×【假设节点】的下标=2×[(2x−1−1)+a]=2x−2+2a∴【左节点】的下标=(2x−1)+2a=2×【假设节点】的下标+1
右节点下标,只需在左节点下标基础上 + 1,即:
2
i
+
2
2i + 2
2i+2
最大堆(特殊的二叉树)
二叉树:每个节点最多有两个子节点
二叉堆:任意节点的值都大于等于(或小于等于)其左右子节点的值;
最大堆:任意节点的值,都大于等于其左右子节点的值
基本思路:
- 将待排序的元素,构建成一个二叉堆
- 依次将堆顶元素取出来,放到已排序的序列中
- 再将剩余的元素重新构建成一个新的堆
Java 代码实现
public static void heapSort(int[] arr) {
int size = arr.length;
// 构建最大堆
// 中间,但靠近左边
int centerLeft = size / 2 - 1;
for (int i = centerLeft; i >= 0; i--) {
heapify(arr, size, i);
}
// 依次取出堆顶元素,放到已排序的序列中
for (int i = size - 1; i >= 0; i--) {
// 将堆顶元素与最后一个元素交换
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
// 从 size - 1 开始,重新构建最大堆
// heapify 函数中,index 超过 heapSize 的元素,将会被忽略比较
heapify(arr, i, 0);
}
}
// 以 nodeIndex 为根节点的子树构建成最大堆(上浮)
public static void heapify(int[] arr, int heapSize, int nodeIndex) {
int largest = nodeIndex; // 初始化最大值为根节点
int left = 2 * nodeIndex + 1; // 左子节点
int right = 2 * nodeIndex + 2; // 右子节点
// 如果左子节点比根节点大,则更新最大值为左子节点
if (left < heapSize && arr[left] > arr[largest]) {
largest = left;
}
// 如果右子节点比最大值还大,则更新最大值为右子节点
if (right < heapSize && arr[right] > arr[largest]) {
largest = right;
}
// 如果最大值不是根节点,则交换根节点和最大值,继续递归构建最大堆
if (largest != nodeIndex) {
int temp = arr[nodeIndex]; // nodeIndex 为原来最大值的位置
arr[nodeIndex] = arr[largest]; // nodeIndex 修改为现在最大值的位置
arr[largest] = temp; // largest 为【小的】位置
heapify(arr, heapSize, largest); // 继续对【小的】,进行 heapify
}
}
public static void main(String[] args) {
int[] arr = {12, 11, 13, 5, 6, 7};
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
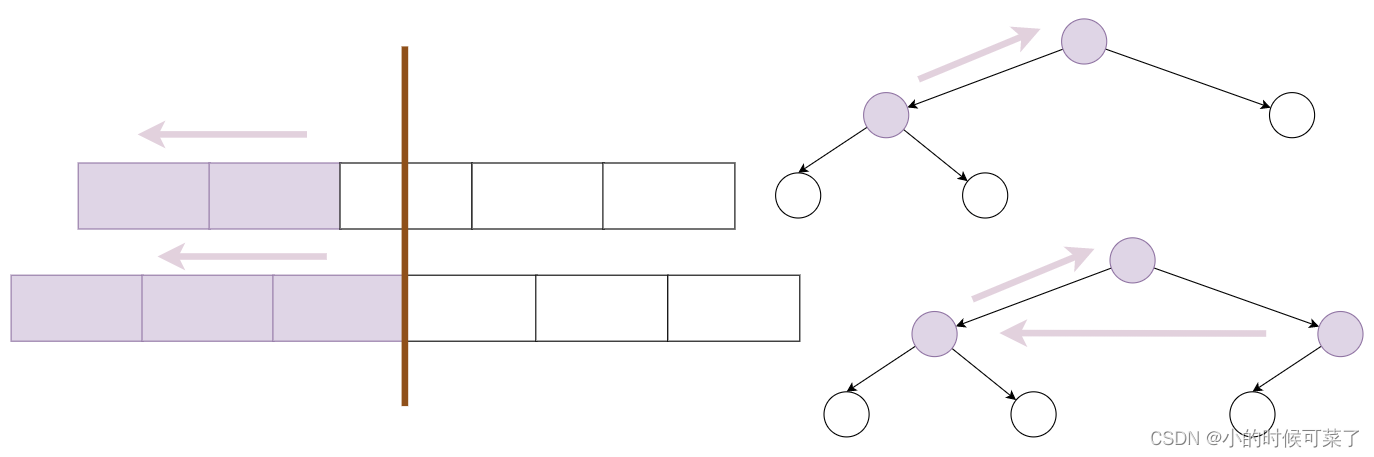
构建最大堆时,中间,但靠近左边的解释:
紫色的为要堆化的元素