文章目录
- 哈希表
- 哈希表 =>红黑树
- —1—> 哈希表缺点
- —2—> 二维数组
- —3—> 数组加链表
- —4—> 树
- —5—> 有序二叉树
- —6—> 平衡二叉树
- —7—> 多叉树
- —8—> 红黑树
- 红黑树的特点
- 红黑树和链表的选择
————————————————————————————————
哈希表
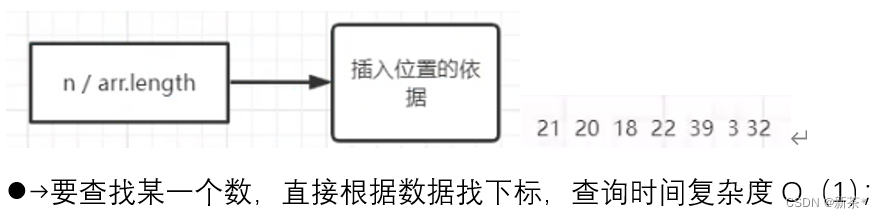
哈希表 =>红黑树
—1—> 哈希表缺点
哈希表查询速度快但是有风险,后来插入数据可能会覆盖原来的数据
—2—> 二维数组
二维数组可以防覆盖,但是数组的大小在创建的时候已经固定,因此同一列插入的数据有限
—3—> 数组加链表
所以使用数组加链表的形式存储数据
—4—> 树
链表降低时间复杂度:树
—5—> 有序二叉树
有序二叉树(左子树比父节点小,右子树比二叉树大)
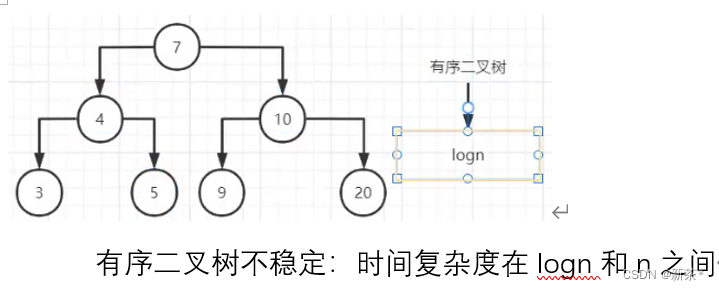
—6—> 平衡二叉树
让有序二叉树稳定:平衡二叉树
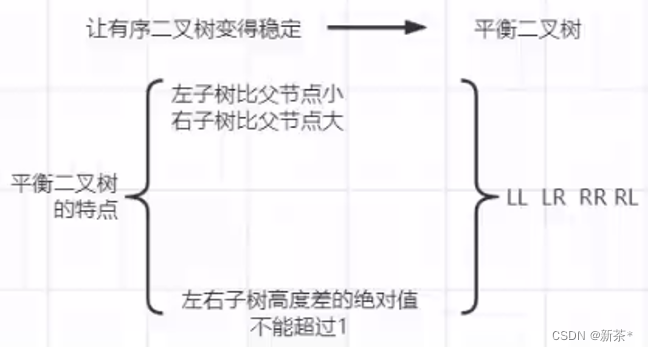
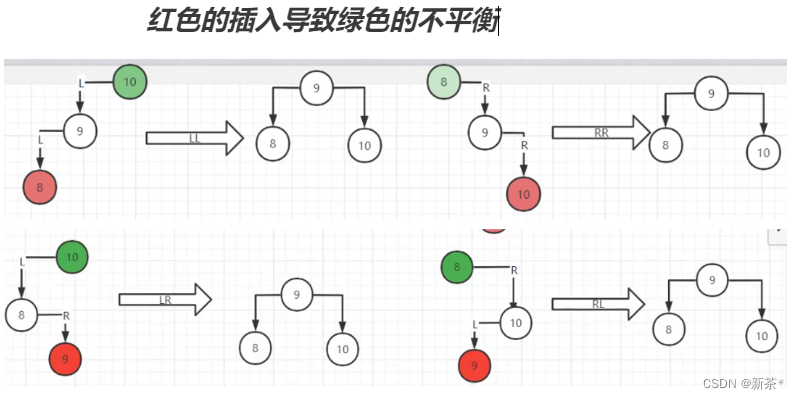
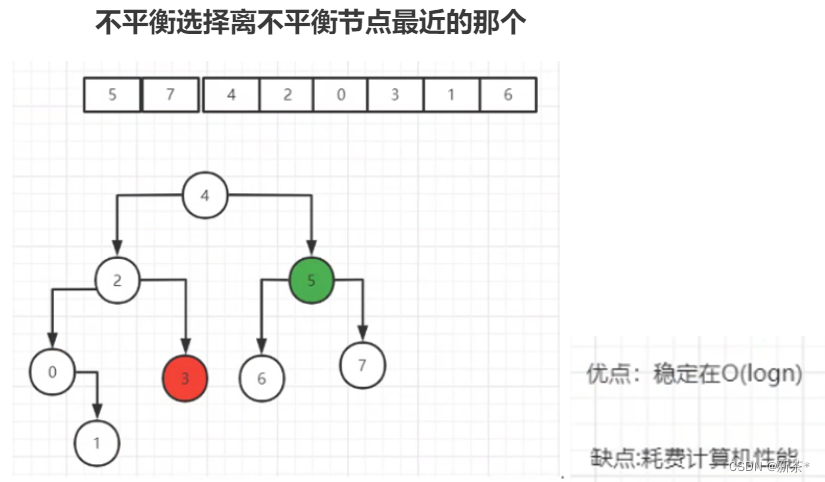
—7—> 多叉树
解决耗费计算机性能:多叉树 2-3-4树(从下往上构建)
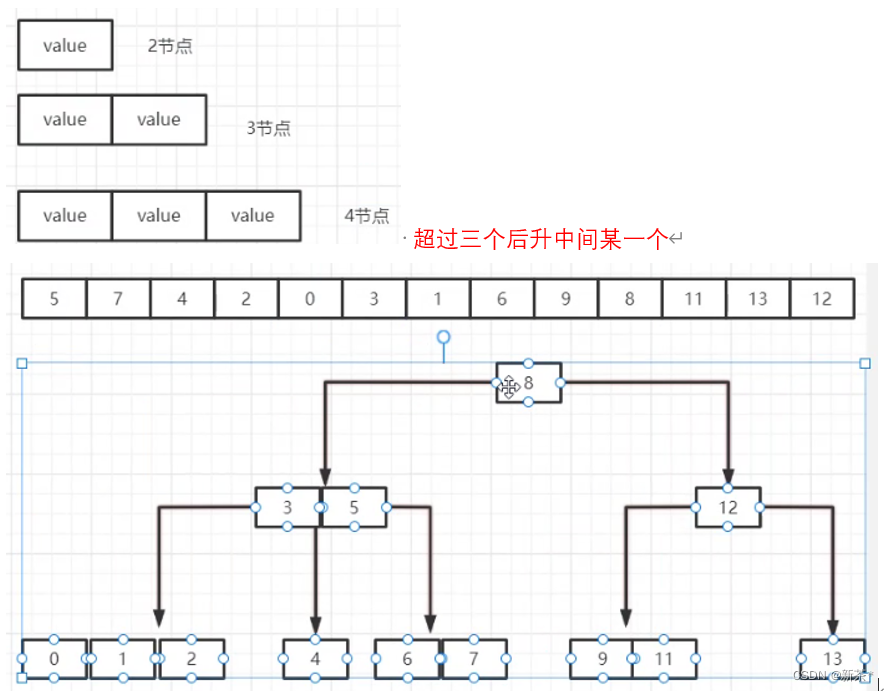
—8—> 红黑树
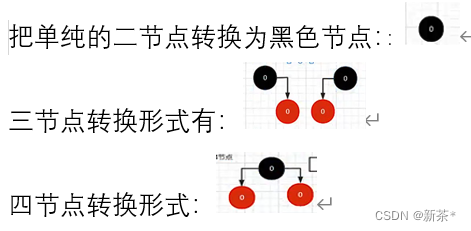
红黑树的特点
(1)节点不是红色就是黑色
(2)在红黑树当中,根节点一定是黑色——>因为在转换过程中,二、三、四节点都是黑色节点开头;
(3)叶子节点一定是黑色的——>有默认的黑色叶子节点,省略没画出来;
(4)从根节点到所有叶子节点 所走的路径上,包含相同数量的黑色节点——>因为在二三四树构建红黑树的过程中,每一层的开头的节点都是黑色节点,黑色节点数目可以代表层数,二三四树的层数相同(等高);
(5)如果一个节点是红色的,那么他的子节点一定是黑色的——>黑色节点开头,红色节点一定是接新节点,所以红色节点一定接黑色节点——>绝对没有成对出现的红色节点——>最复杂的路线是黑红相间,最短的路径都是黑色——>最长的路径绝不会超过最短路径的二倍——>红黑树相对于有序二叉树的稳定性
红黑树解决了不稳定的问题,解决了资源消耗的问题,是内存最优二叉树
红黑树和链表的选择
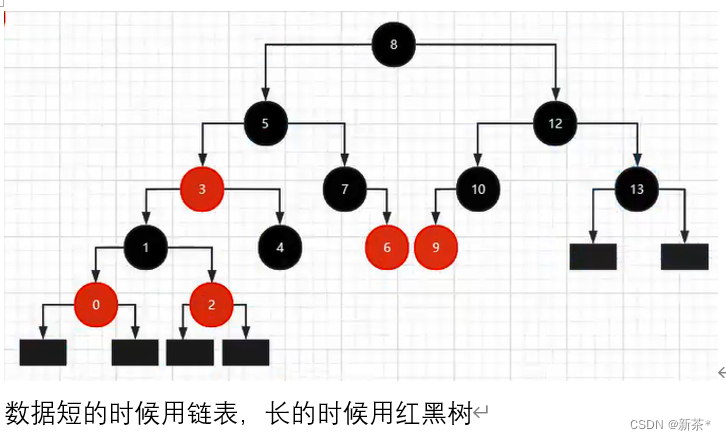

![[附源码]计算机毕业设计人体健康管理appSpringboot程序](https://img-blog.csdnimg.cn/ac5fad3e96844184a2ef4186c86dd463.png)



![MyBatis-Plus之ActiveRecord[基础增删改查操作]](https://img-blog.csdnimg.cn/6682f916db1a40e387760a77f762e8ba.png)




![[附源码]计算机毕业设计时间管理软件appSpringboot程序](https://img-blog.csdnimg.cn/e9015a84b3044aa298d5156ff04147e2.png)