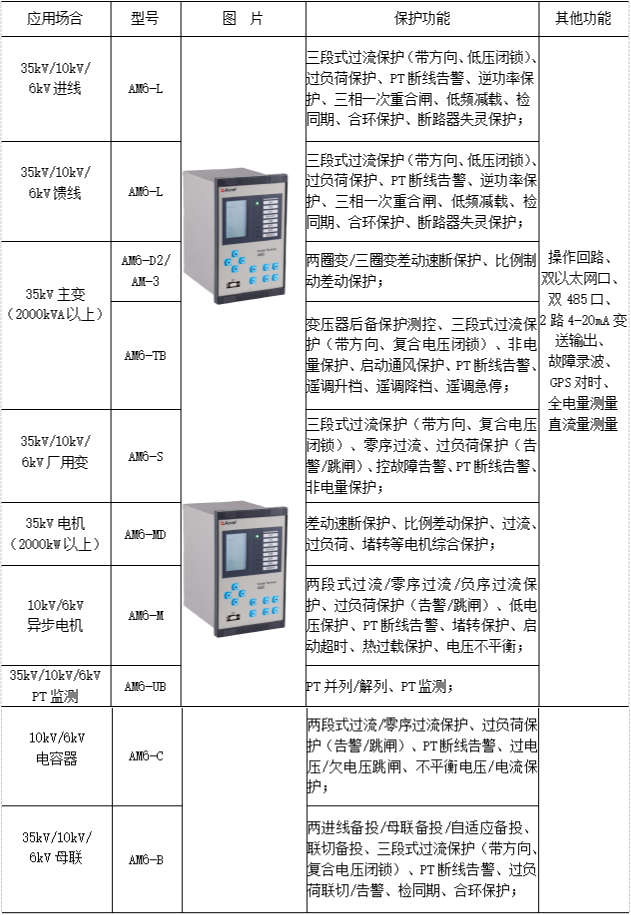
x.1 Linear Regression Theory

x.1.1 Model

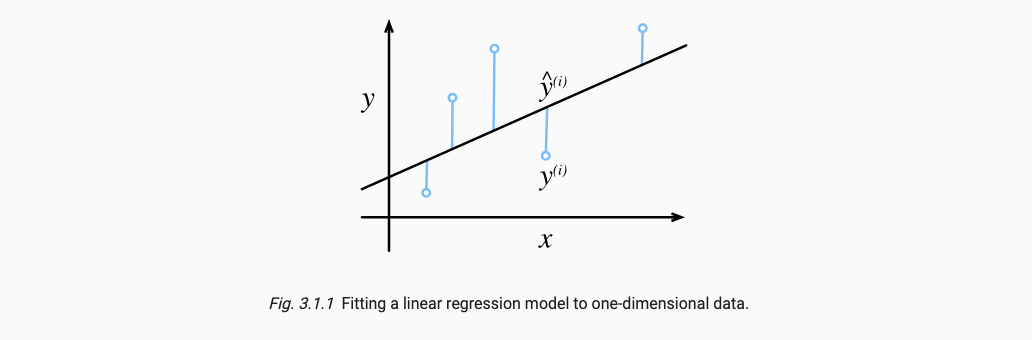
线性回归的模型如下：

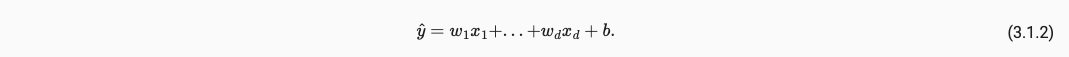
我们给定d个特征值$x_1,x_2,...,x_d$，最终产生输出yhat，我们产生的yhat要尽量拟合原来的值y，在这一拟合过程中我们通过不断修改$w_1,...,w_d和b$来实现。

x.1.2 Stategy or Loss

如何评价这个拟合好不好呢，我们的loss/strategy选择为MSE，对于单个点的损失如下：

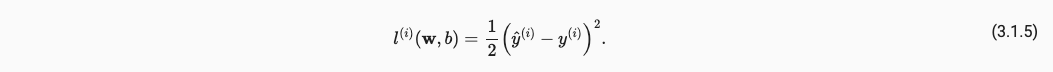
将全部的点都添加至损失，得到，

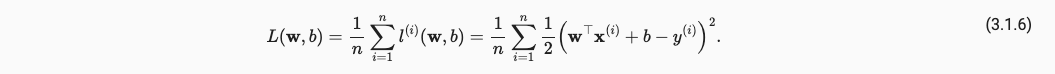
最终我们需要做的就是最小化Loss，如下：

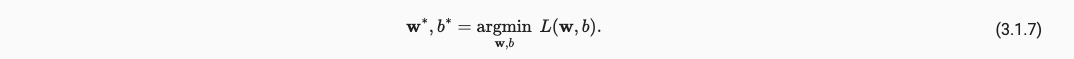
x.1.3 Algorithm

我们使用什么algorithm/optimizer来最小化loss呢？这里采用了Minibatch Stochastic Gradient Descent，mini-batch SGD也是深度学习中最常用的方法。

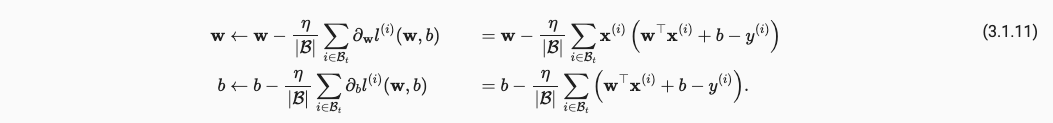
x.1.4 Nerual Network

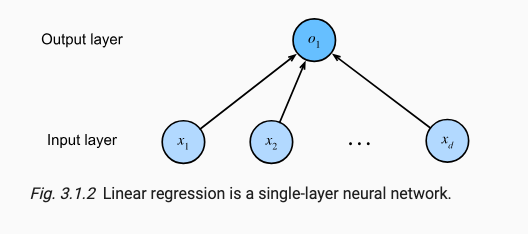
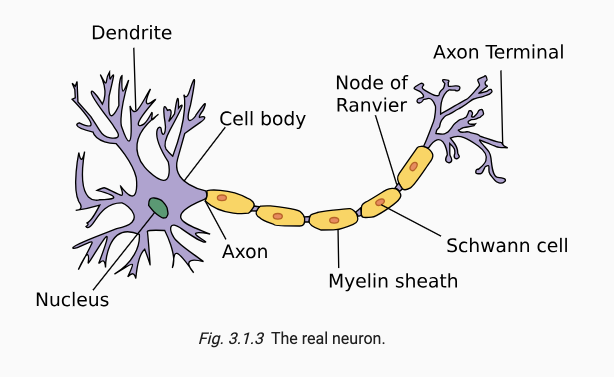
线性回归的过程类似于神经元的表达，多个输入产生一个输出，

x.2 Experiments

x.2.1 手撕一个Linear Regression*

在下面的内容中，只使用了torch的自动微分来实现Linear Regression，值得反复推敲。

'''
手撕一个线性回归，包括：
1. 构造真实线性回归式子
2. 初始化权重
3. 生成一个迭代器每次取batch_size个数据
4. 构造model线性回归
5. 构造cost funtion-MSE
6. 构造optimizer-SGD
7. 开始每个epoch的训练, 注意梯度何时更新: 
        先loss(model(), y)计算loss来构造计算图; backward()计算梯度参数grad; param-=lr*grad更新梯度; param.zero_()梯度变零; 循环。

线性回归简洁表示:

这其实是一个feature=2, n=1000, label.shape=1的二元线性回归问题y = a * x_1 + b * x_2 + c: 用1000个样本(x_1, x_2)来拟合出a, b, c.
线性回归的简洁实现
'''
import random
import torch


# 生成n = 1000组数据, label 1维, features 2维; => weight [2, 1]
# 初始化 weight 和 bias 的初始值
def synthetic_data(w, b, num_examples): 
    """⽣成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b 
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))


true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

print('features:', features[0],'\nlabel:', labels[0])


# 手撕一个DataLoader
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]

# 让我们尝试使用iter取batch_size个data
batch_size = 10
for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

# 初始化权重，并使用`requires_grad=True`开启其自动微分
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True) 
b = torch.zeros(1, requires_grad=True)

#  model
def linreg(X, w, b):
    """线性回归模型"""
    # return torch.matmul(X, w) + b
    return X.mm(w) + b

# cost function
def squared_loss(y_hat, y):
    """MSE"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

# optimizer to minimize cost function
def sgd(params, lr, batch_size):
    """mini batchsize SGD"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()


# 设置超参数
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss


# 开始训练
for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y) # X和y的⼩批量损失
        # 因为l形状是(batch_size,1)，⽽不是⼀个标量。l中的所有元素被加到⼀起，
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size) # 使⽤参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')


print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

在这里补充一下with torch.no_grad()，这个函数用于在上下文中取消梯度更新。详见https://blog.csdn.net/qq_43369406/article/details/131115578

x.2.2 Concise Implementation of Linear Regression 简明实现

在model部分，由于Linear线性层由于经常需要使用到，故现代Pytorch已经将其封装为了一个API函数即torch.nn.LeazyLinear。这个API只关注输出的全连接层的结点个数。

在Loss部分，用torch.nn.MSELoss代替。

在Optimizer部分，用torch.optim.SGD代替。

import numpy as np
import torch
from torch import nn
from d2l import torch as d2l


"""
1. define model

"""
class LinearRegression(d2l.Module):  #@save
    """The linear regression model implemented with high-level APIs."""
    def __init__(self, lr):
        super().__init__()
        self.save_hyperparameters()
        self.net = nn.LazyLinear(1) # The latter allows users to only specify the output dimension | Specifying input shapes is inconvenient
        self.net.weight.data.normal_(0, 0.01)
        self.net.bias.data.fill_(0)

# 使用bulit-in func `__call__` 实现forward
@d2l.add_to_class(LinearRegression)  #@save
def forward(self, X):
    return self.net(X)

"""
2. define loss

"""
@d2l.add_to_class(LinearRegression)  #@save
def loss(self, y_hat, y):
    fn = nn.MSELoss()
    return fn(y_hat, y)

"""
3. define optimizer

"""
@d2l.add_to_class(LinearRegression)  #@save
def configure_optimizers(self):
    return torch.optim.SGD(self.parameters(), self.lr)

"""
4. training

"""
model = LinearRegression(lr=0.03)
data = d2l.SyntheticRegressionData(w=torch.tensor([2, -3.4]), b=4.2)
trainer = d2l.Trainer(max_epochs=3)
trainer.fit(model, data)

@d2l.add_to_class(LinearRegression)  #@save
def get_w_b(self):
    return (self.net.weight.data, self.net.bias.data)
w, b = model.get_w_b()

print(f'error in estimating w: {data.w - w.reshape(data.w.shape)}')
print(f'error in estimating b: {data.b - b}')

3.3 欠拟合过拟合

待学习

3.4 权重衰减

待学习