简介

Megatron-LM是一个基于PyTorch的框架，用于训练基于Transformer架构的巨型语言模型。它实现了高效的大规模语言模型训练，主要通过以下几种方式：

• 模型并行：将模型参数分散在多个GPU上，减少单个GPU的内存占用23。
• 数据并行：将数据批次分散在多个GPU上，增加训练吞吐量4。
• 混合精度：使用16位浮点数代替32位浮点数，减少内存和带宽需求，提高计算速度
• 梯度累积：在多个数据批次上累积梯度，然后再更新参数，降低通信开销
• Megatron-LM还可以与其他框架如DeepSpeed结合，实现更高级的并行技术，如ZeRO分片和管道并行5。这样可以进一步提升训练效率和规模。

超大规模语言模型训练 = GPU + PyTorch + Megatron-LM + DeepSpeed

3D并行

前置知识点：通信算子

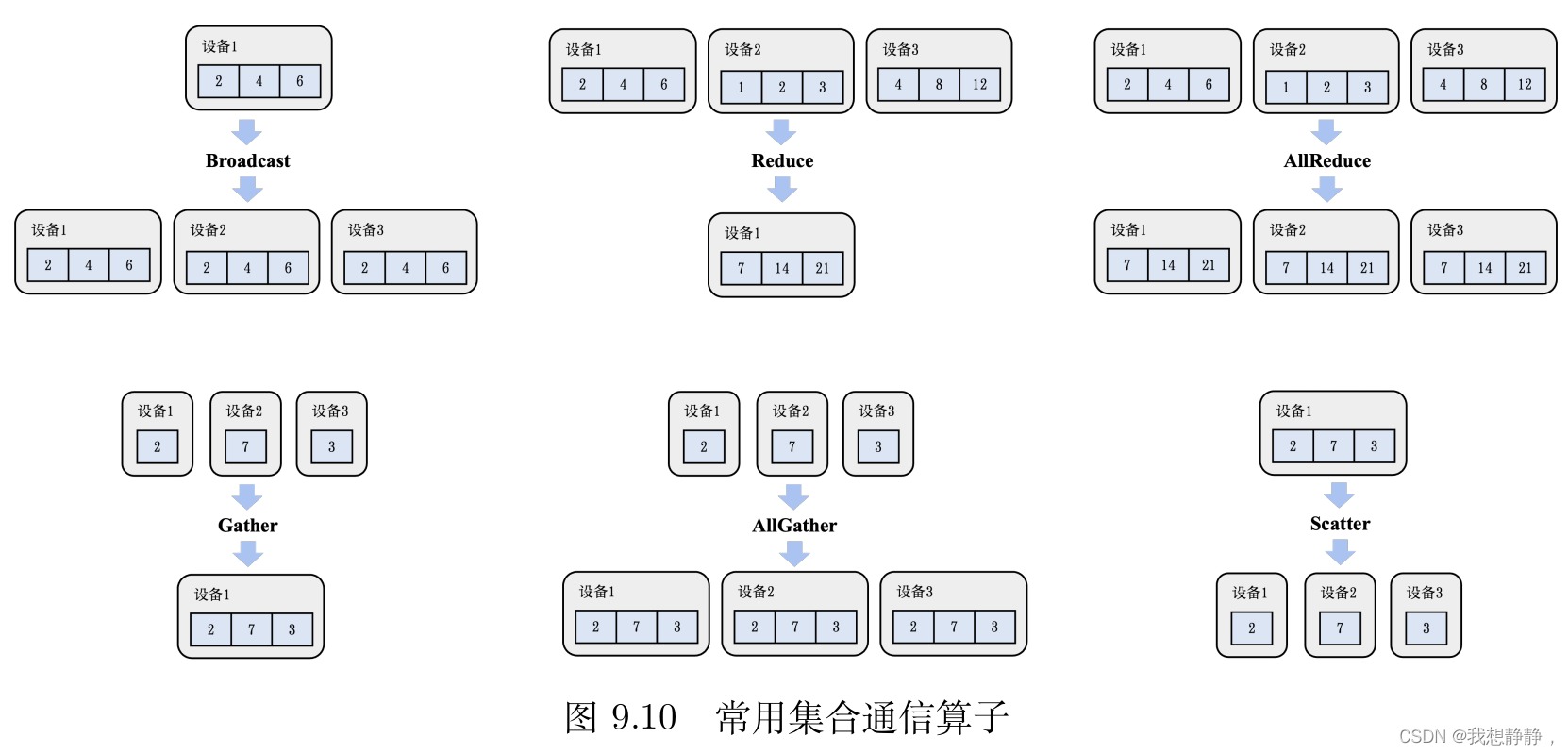
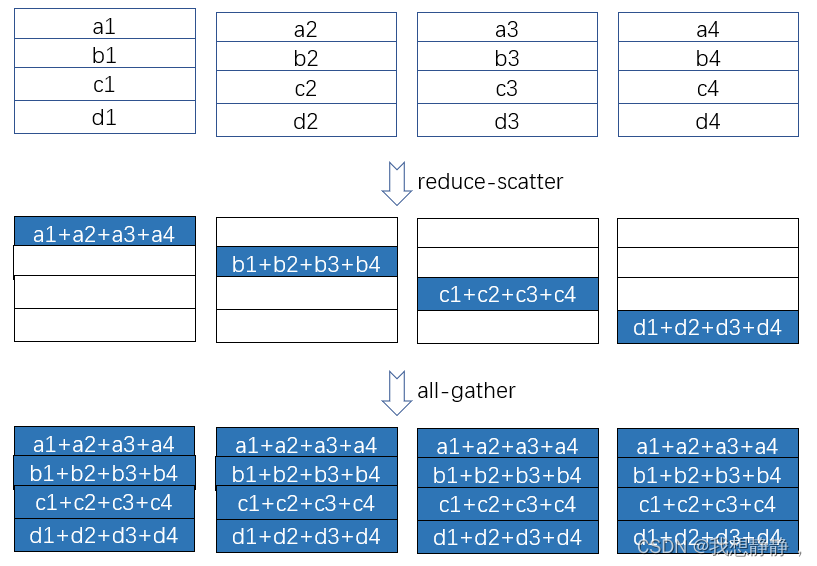
其中 all-reduce = reduce-scatter + all-gather

1. DP 数据并行

每批输入的训练数据都在数据并行的 worker 之间平分。反向传播后需要通信并规约梯度，以保证优化器在各个 worker 上进行相同的更新。

显存效率优化（ZeRO ）

数据并行会在所有 worker 之间进行模型参数和优化器的复制，因此显存效率不高。DeepSpeed 开发了 ZeRO ，它是一系列用于提高数据并行的显存效率的优化器。 这项工作依赖于 ZeRO 的 1 阶段，该阶段在 worker 之间划分优化器状态量以减少冗余。

混合精度训练和Adam优化器是训练语言模型的标配。Adam在SGD基础上，为每个参数梯度增加了一阶动量（momentum）和二阶动量（variance）。混合精度训练同时存在fp16和fp32两种格式的数值，其中模型参数、模型梯度都是fp16，此外还有fp32的模型参数（用于计算更新量，防止精度截断），如果优化器是Adam，则还有fp32的momentum和variance。

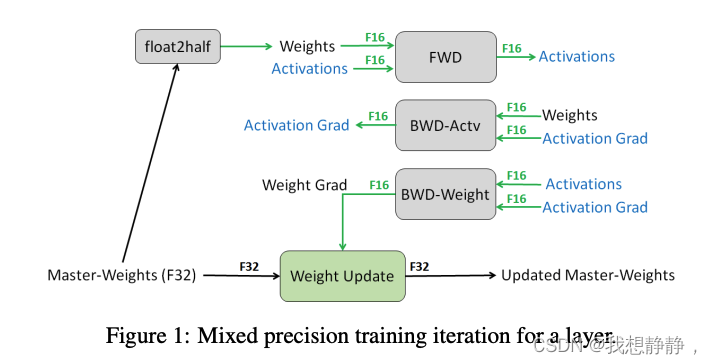
在模型训练阶段，每张卡中显存内容分为两类：

1. 模型状态（model states）: 模型参数（fp16）、模型梯度（fp16）和Adam状态（fp32的模型参数备份，fp32的momentum和fp32的variance）。假设模型参数量 $\varphi$，则共需要 $2\Phi +2\Phi +(4\Phi +4\Phi +4\Phi )=4\Phi +12\Phi =16\Phi$字节存储，可以看到，Adam状态占比 75% 。
2. 剩余状态（residual states）: 除了模型状态之外的显存占用，包括激活值（activation）、各种临时缓冲区（buffer）以及无法使用的显存碎片（fragmentation）。

每张卡的模型状态冗余内容过多，ZeRO使用分片，即每张卡只存 $\frac{1}{N}$的模型状态量，这样系统内只维护一份模型状态。

1. Zero-1：首先进行分片操作的是模型状态中的Adam，模型参数（parameters）和梯度（gradients）仍旧是每张卡保持一份，此时，每张卡的模型状态所需显存是$4\Phi +\frac{12\Phi }{N}$字节，当 N 比较大时，趋向于 $4\Phi$，也就是原来 $16\Phi$的 $\frac{1}{4}$。
2. Zero-2：继续对模型梯度进行分片，模型参数仍旧是每张卡保持一份，此时，每张卡的模型状态所需显存是 $2\Phi +\frac{2\Phi +12\Phi }{N}$字节，当 N比较大时，是原来的$\frac{1}{8}$。
3. Zero-3：继续对模型参数进行分片，此时每张卡的模型状态所需显存是 $\frac{16\Phi }{N}$字节 。

对剩余状态，也就是激活值（activation）、临时缓冲区（buffer）以及显存碎片（fragmentation）的优化：

1. 激活值同样使用分片方法，并且配合checkpointing
2. 模型训练过程中经常会创建一些大小不等的临时缓冲区，比如对梯度进行AllReduce啥的，解决办法就是预先创建一个固定的缓冲区，训练过程中不再动态创建，如果要传输的数据较小，则多组数据bucket后再一次性传输，提高效率
3. 显存出现碎片的一大原因是时候gradient checkpointing后，不断地创建和销毁那些不保存的激活值，解决方法是预先分配一块连续的显存，将常驻显存的模型状态和checkpointed activation存在里面，剩余显存用于动态创建和销毁discarded activation

通信分析：
传统数据数据并行在每一步（step/iteration）计算梯度后，需要进行一次AllReduce操作来计算梯度均值，目前常用的是Ring AllReduce，分为ReduceScatter和AllGather两步，每张卡的通信数据量（发送+接受）近似为$2\Phi$

对于Zero-1，当通过计算好梯度均值后，就可以更新局部的优化器状态（包括 $\frac{1}{N}\Phi$的参数），当反向传播过程结束，进行一次Gather操作，更新 $(1-\frac{1}{N})\Phi$的模型参数，通信总数据量是 $\Phi$ 。相当于用Reduce-Scatter和AllGather两步，和数据并行一致。

对于Zero-2，各个gpu为了计算它这 $\frac{1}{N}$梯度的均值，需要进行一次Reduce操作，通信数据量是 $\frac{1}{N}\Phi \cdot N=\Phi$，然后其余显卡则不需要保存这部分梯度值了。

对于Zero-3，每张卡只存了局部的参数，不管是在前向计算还是反向传播，都涉及一次Broadcast操作。

ZeRO-Offload:
在GPU上面进行前向和后向计算，将梯度传给CPU，进行参数更新，再将更新后的参数传给GPU。为了提高效率，可以将计算和通信并行起来，GPU在反向传播阶段，可以待梯度值填满bucket后，一边计算新的梯度一边将bucket传输给CPU，当反向传播结束，CPU基本上已经有最新的梯度值了，同样的，CPU在参数更新时也同步将已经计算好的参数传给GPU

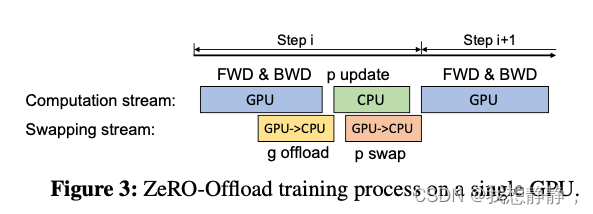
DeepSpeed之ZeRO系列：将显存优化进行到底 - basicv8vc的文章 - 知乎
https://zhuanlan.zhihu.com/p/513571706

计算效率优化（梯度累计减少通信）

随着我们提高并行度，每个 worker 执行的计算量是恒定的。数据并行可以在小规模上实现近乎线性扩展。但是，在 worker 之间规约梯度的通信开销跟模型大小成正相关，所以当模型很大或通信带宽很低时，计算效率会受限。

梯度累积是一种用来均摊通信成本的一种常用策略。它会进一步增加batch大小，在本地使用 micro-batch 多次进行正向和反向传播积累梯度后，再进行梯度规约和优化器更新。

2. TP tensor并行（算子内）

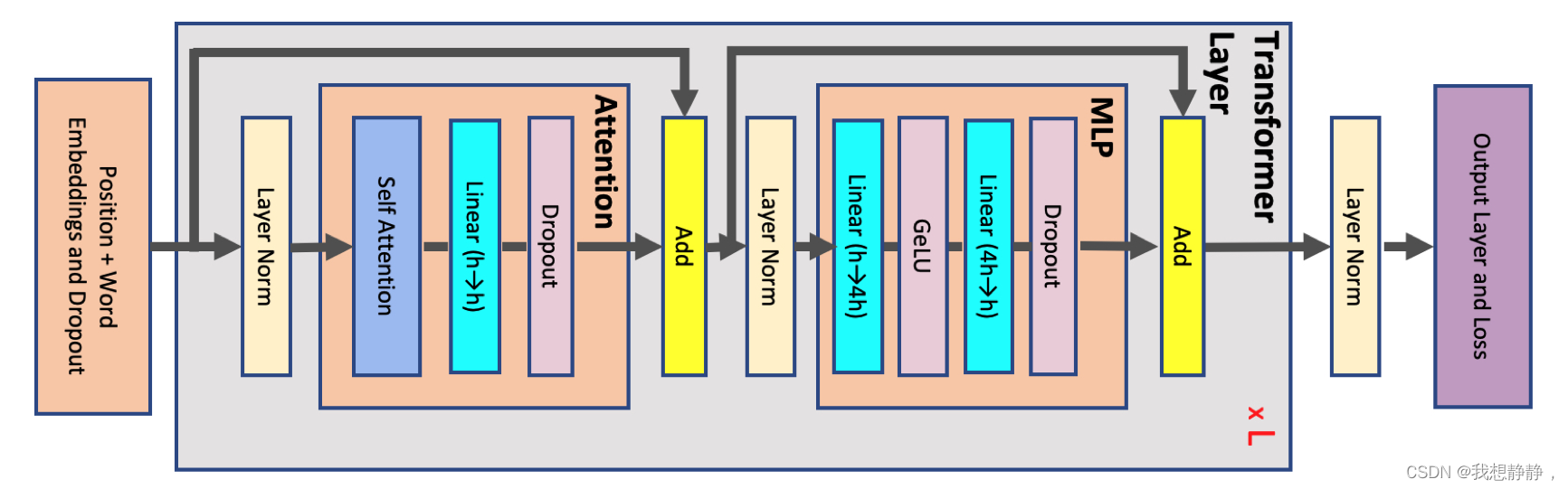
transformer主要由两部分组成：Attention模块和MLP模块。Megatron-LM分别对这两部分都进行了并行，另外对输入输出的embedding也做了并行。

设b 为 batch size，s 为 sequence length，h 为 hidden size，n 为 num head，p 为切分数，v是字典大小，

前置知识点：矩阵分块并行计算

对矩阵乘法进行并行化本质上是分块矩阵乘法。这里以二维矩阵为例，当我们要将矩阵进行分块时，有两种分法，横切（row）和竖切（column）。

$XA=Y$矩阵乘法可以分为两种切分方法

纵切 $X[A1,A2]=cat(XA1,XA2)=[XA1，XA2]$

横切 $[X1,X2][A1,A2{]}^T=add(X1A1,X2A2)=X1A1+X2A2$

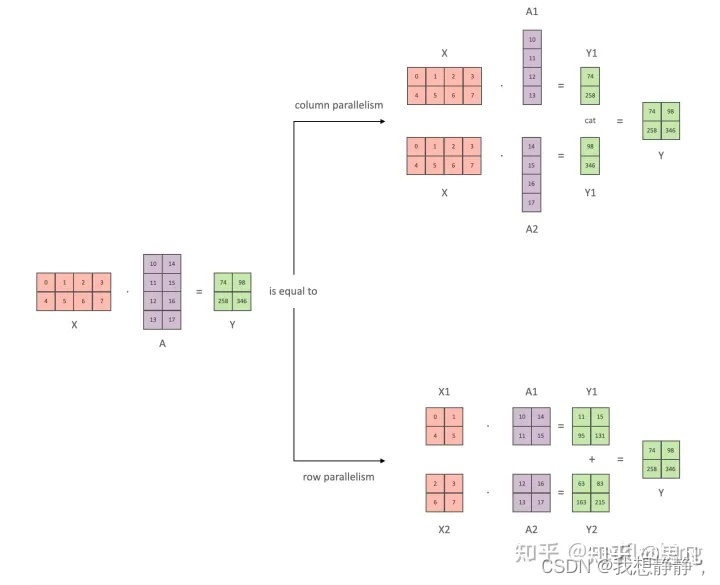
MLP

MLP 模块本质上就是矩阵乘法。

MLP的整个计算过程给抽象为下述数学表达式：
$Y=Gelu(XA),Z=Dropout(YB)$

• 对A纵切，$X[A1,A2]=cat(XA1,XA2)=[XA1，XA2]，Y=[Gelu(XA1),Gelu(XA2)]$此时虽然Gelu是非线性函数，但是不影响结果。
• 对A横切， $[X1,X2][A1,A2{]}^T=add(X1A1,X2A2)=X1A1+X2A2，Y=Gelu(X1A1+X2A2)$ 也就是在Gelu前，需要对结果做all-reduce。

所以选用对A进行纵切，这样就少了一次all-reduce操作。

上一步纵切并行计算后，得到$Y=[Y1,Y2]$,

• 对B纵切的话，需要通信得到完整Y。
• 对B横切的话， $[Y1,Y2][B1,B2{]}^T=add(Y1B1,Y2B2)=Y1B1+Y2B2，Y=Dropout(Y1B1+Y2B2)$ 所以仅需Dropout前做all-reduce

所以选择对B纵切，这样整个MLP前向传播仅需一次all-reduce，在向后传递中执行一次all-reduce操作。

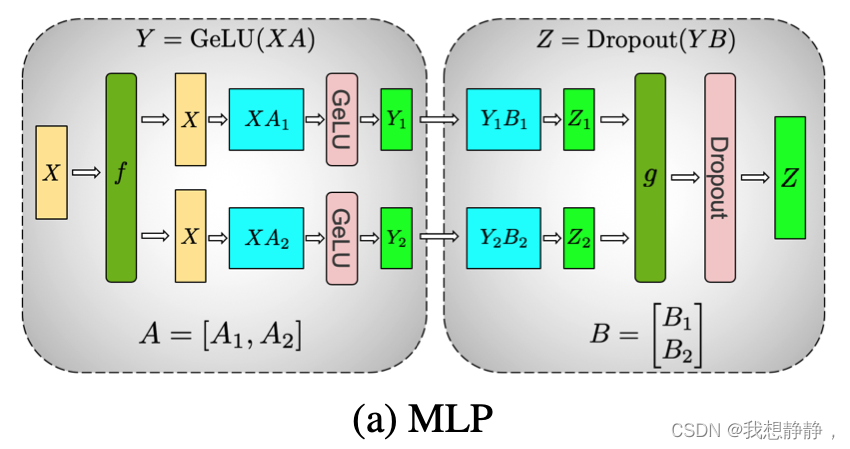
原mlp 的计算如下：
$$\begin{gathered} [b,s,h]\times [h,4h]=[b,s,4h] \\ [b,s,4h]\times [4h,h]=[b,s,h] \end{gathered}$$

将 [h, 4h] 切分成 [h, 4h/p]，把 [4h, h] 切分成 [4h/p, h]，对[b, s, h]复制到p个卡上。计算步骤变为：
$$\begin{gathered} [b,s,h]\times [h,4h/p]=[b,s,4h/p] \\ [b,s,4h/p]\times [4h/p,h]=[b,s,h] \end{gathered}$$
此有 p 个 [b, s, h]，需要做一次 allreduce 得到最终的 [b, s, h]

self-attention

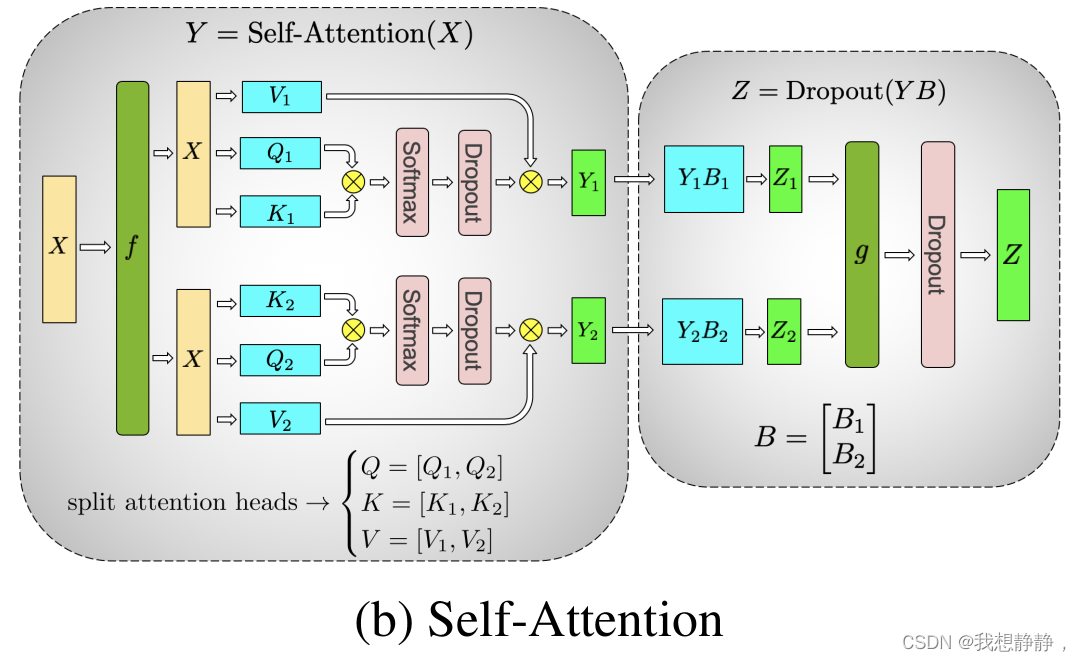
self attention 的计算如下：

1. $[b,s,h]\times [h,3h]=[b,s,3h]$
2. [b, s, 3h] 从最后一维被分为 3 组，被称为 Q, K, V，每组是 n 个 [b, s, h/n]
3. Q、K 两组对应的项做乘法，也就是 n 个 $[b,s,h/n]\times [b,s,h/n{]}^T=[b,s,h/n]\times [b,h/n,s]=[b,s,s]$
4. 得到的 n 个 [b, s, s] 和对应的 V 做乘法，得到 n 个 $[b,s,s]\times [b,s,h/n]=[b,s,h/n]$
5. n 个 [b, s, h/n] concat 到一起，得到 [b, s, h]
6. $[b,s,h]\times [h,h]=[b,s,h]$

self attension 中的参数为 [h, 3h] 和 [h, h]。同理对[h, 3h] 纵向切分成 [h, 3h/p]，把 [h, h] 横向切分成 [h/p, h]，对[b, s, h]复制到p个卡上。计算步骤如下：

1. $[b,s,h]\times [h,3h/p]=[b,s,3h/p]$
2. [b, s, 3h/p] 被分为 3 组，即 Q, K, V，每组 n/p 个 [b, s, h/n] (这里是一个head生成的q/k/v的尺寸，所以每个gpu上有3n/p 个 [b, s, h/n] ，假如p=n，就是一个gpu处理一个头)
3. Q、K 两组对应的项做乘法，也就是 n/p 个 $[b,s,h/n]\times [b,s,h/n{]}^T=[b,s,h/n]\times [b,h/n,s]=[b,s,s]$
4. 得到的 n/p 个 [b, s, s] 和对应的 V 做乘法，得到 n/p 个 $[b,s,s]\times [b,s,h/n]=[b,s,h/n]$
5. n/p 个 [b, s, h/n] concat 到一起，得到 [b, s, h/p] （这里n>p???）
6. $[b,s,h/p]\times [h/p,h]=[b,s,h]$
7. 注意这时每张卡上都有一份 [b, s, h]，需要对这 p 个 [b, s, h] 做一次 allreduce 得到最终的 [b, s, h]

embedding层

torch将embedding视为将input作为index，在weight上做index_select操作，实际上embedding也可以被视为，对input进行one_hot然后和weight进行mm的操作，所以将embedding层做为linear层使用模型并行操作。

原输入操作

1. 输入尺寸[b, s]，字典大小[v, h]
2. [b, s]在[v, h]中查找，得到结果[b, s, h]

并行化，将[v, h]横向切分，各个卡保留[v/p, h]：

1. 将输入[b, s]复制到p张卡上，在p个[v/p, h]中查找，得到p个[b, s, h] （找不到的填0）
2. 对p个[b, s, h] 执行all-reduce

原输出操作

1. 输出尺寸[b, s, h]，字典大小[v, h]
2. $[b,s,h]\times [v,h{]}^T=[b,s,v]$
3. [b, s, v] = softmax([b, s, v])

并行化：

1. 输出[b, s, h]复制到p张卡上
2. 得到p个$[b,s,h]\times [v/p,h{]}^T=[b,s,v/p]$
3. p个[b, s, v/p]分别计算指数$e^i$并求和，得到p个[b, s, 1]
4. 对p个[b, s, 1]执行all-reduce，各个卡上都有了指数和[b, s, 1]
5. 对p个指数[b, s, v/p]除以指数和[b, s, 1]得到softmax值

小节

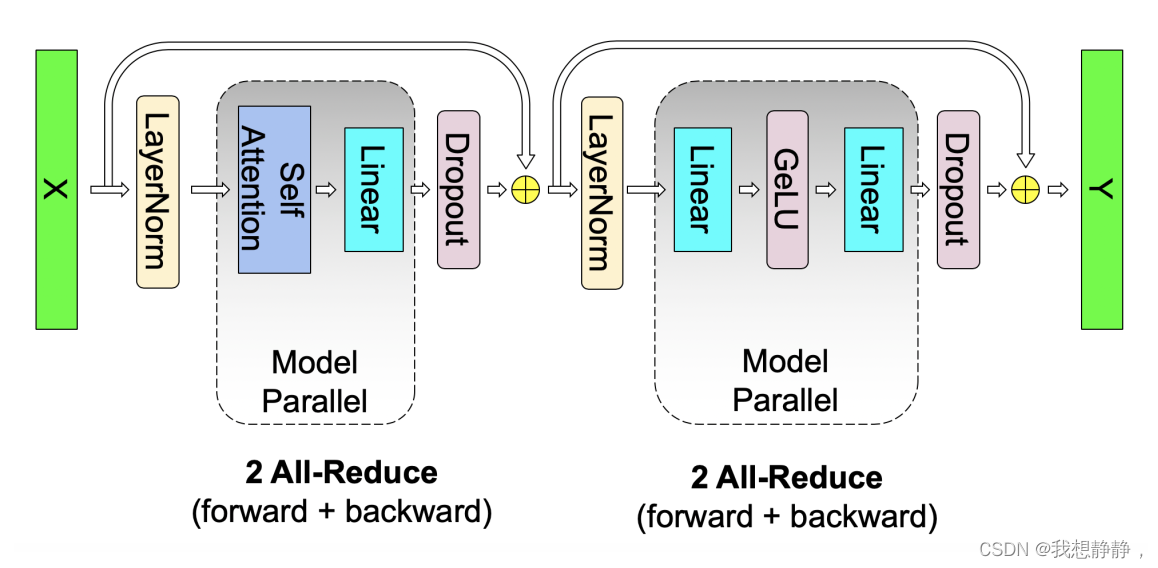对于单个transformer层，仅需要在forward和backward时分别有两个all-reduce

3. PP pipeline并行（算子间）

算子间进行切分，分配到不同gpu

流水线并行将模型的各层划分为可以并行处理的阶段。当一个阶段完成一个 micro-batch 的正向传递时，激活内存将被通信至流水线的下一个阶段。类似地，当下一阶段完成反向传播时，将通过管道反向通信梯度。

• 必须同时计算多个 micro-batch 以确保流水线的各个阶段能并行计算。
• 目前已经开发出了几种用于权衡内存和计算效率以及收敛行为的方法，例如 PipeDream。DeepSpeed 采用的方法是通过梯度累积来实现并行，并保持与传统数据并行和模型并行训练在相同的总 batch 大小下收敛情况相同。

  例如：反向传播时，设备4开始第1个微批量的反向传播任务。该任务完成后的中间结果会被发送给设备3，触发响应的反向传播任务。与此同时，设备4会缓存好对应第1个微批量的梯度，接下来开始第2个微批量计算。当设备4完成了全部的反向传播计算后，他会将本地缓存的梯度进行相加，并且除以微批量数量，计算出平均梯度，该梯度用于更新模型参数。

显存效率：

• 流水线并行减少的显存与流水线的阶段数成正比，使模型的大小可以随 worker 的数量线性扩展。
• 但是流水线并行不会减少每一层的激活函数的显存占用量。此外，每个 worker 必须存储同时运行的各个 micro-batch （整个batch）的激活值。增大batch size就会线性增大需要被缓存激活的显存需求。GPU需要在前向传播至反向传播这段时间内缓存激活(activations)。以GPU0为例，microbatch1的激活需要从整个batch的开始保存至最后。

为了解决显存的问题，使用了gradient checkpointing。该技术不需要缓存所有的激活，而是在反向传播的过程中重新计算激活。这降低了对显存的需求，但是增加了计算代价。

计算效率：

• 流水线并行具有最低的通信量，因为它的通信量只和在各阶段边界的各层的激活值大小成正比。
• 但是，它不能无限扩展。像模型并行一样，增加流水线大小会减少每个流水线阶段的计算量，这会降低计算与通信的比率。
• 如果要实现好的计算效率，流水线并行还要求其每个阶段的计算负载完美的均衡。
• 此外，流水线并行性会在每个 batch 的开始和结束时因为需要重新填充或排空流水线而产生 bubble overhead。使用流水线阶段数的 4 倍或 8 倍的梯度累积步骤（以及 batch 大小）进行训练，相较于只有一个流水线阶段分别达到了 81％ 和 90％ 的扩展性。
  
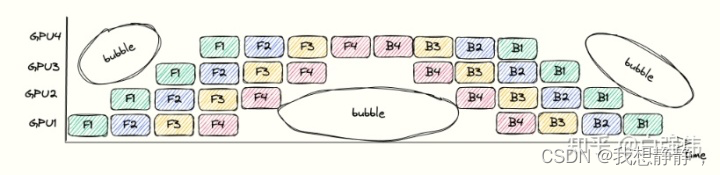
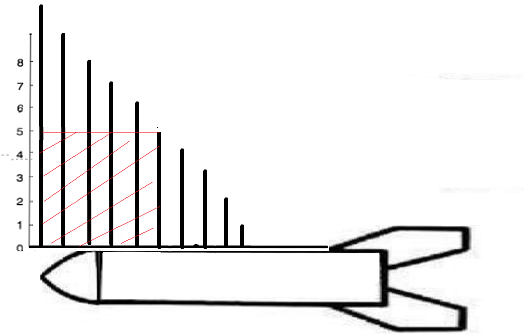
  bubbles浪费时间的比例依赖于pipeline的深度 n 和mincrobatch的数量 m 。假设单个GPU上完成前向传播或者后向传播的面积为1(也就是上图中的单个小方块面积为1)。上图中的总长度为 2(m+n-1) ，宽度为 n，总面积为 2n(m+n-1) 。其中，彩色小方块占用的面积表示GPU执行的时间，为其 2nm。空白处面积的占比代表了浪费时间的比较，其值为$1-\frac{2nm}{2n(m+n-1)}=1-\frac{m}{m+n-1}$。因此，增大microbatch的数量m，可以降低bubbles的比例。

3D并行的合并

合并数据并行和流水线并行

数据并行和流水线并行是正交的，可以同时使用。如下图，水平方向是完整的一个模型（流水线并行），垂直方向是相同层的不同副本（数据并行）。

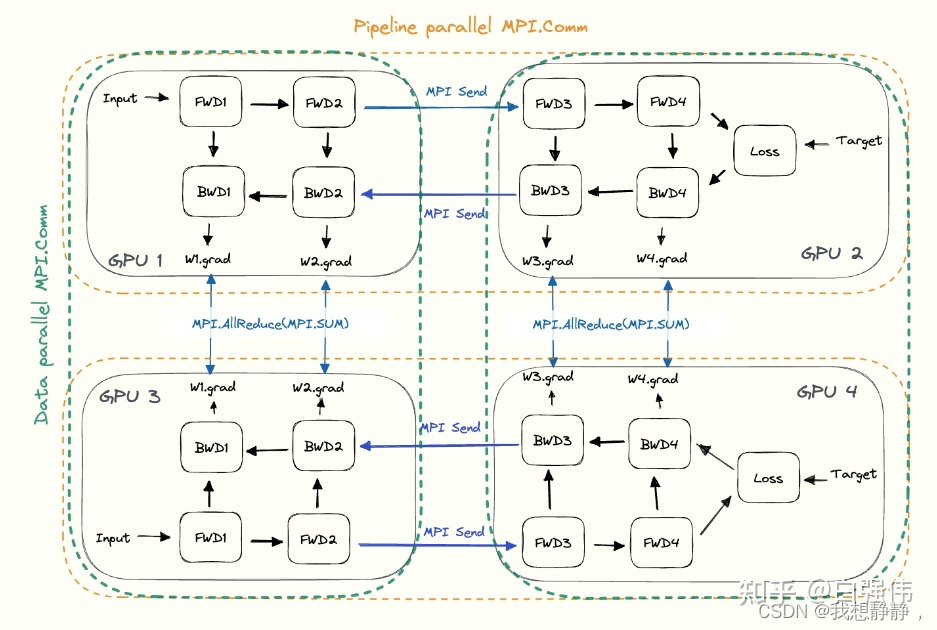
3D混合并行

优化节点内和节点间的通信带宽：

1. tensor并行是这三种策略中通信开销最大的，因此我们优先考虑将tensor并行 worker 组放置在节点内以利用更大的节点内带宽。这里我们基于英伟达 Megatron-LM 进行了张量切分式的tensor并行。
2. 当tensor并行组不占满节点内的所有 worker 时，我们选择将数据并行组放置在节点内。不然就跨节点进行数据并行。
3. 流水线并行的通信量最低，因此我们可以跨节点调度流水线的各个阶段，而不受通信带宽的限制。

通过并行通信增大带宽：

1. 每个数据并行组需要通信的梯度量随着流水线和tensor并行的规模线性减小，因此总通信量少于单纯使用数据并行。
2. 此外，每个数据并行组会在局部的一小部分 worker 内部独立进行通信，组间通信可以相互并行。这样的结果是，通过减少通信量和增加局部性与并行性，数据并行通信的有效带宽被增大了。

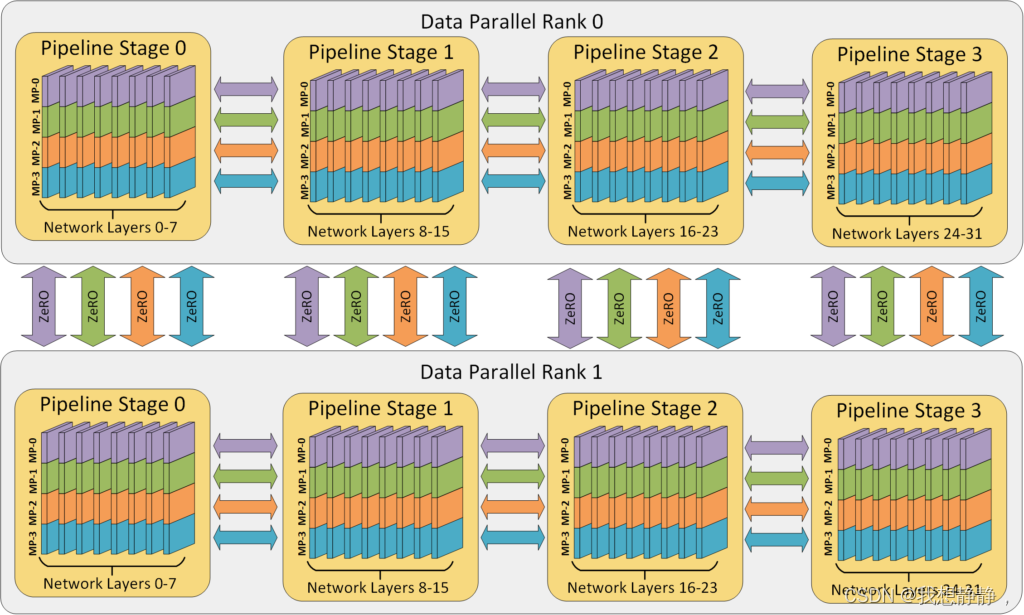
一个有 32 个 worker 进行 3D 并行的例子。神经网络的各层分为四个流水线阶段。每个流水线阶段中的层在四个模型并行 worker 之间进一步划分。最后，每个流水线阶段有两个数据并行实例，且 ZeRO 在这 2 个副本之间划分优化器状态量。

上图 中的 worker 到八个节点（每个节点有四个 GPU）的系统上的 GPU 的映射。同一颜色的 GPU 在同一节点上。

混合精度

FP16 格式由1个符号位，5位指数和10个尾数位组成，指数能表示范围在[-14, 15]之间。FP32 格式由1个符号位，8位指数和23个尾数位组成，指数能表示范围在[-127, 128]之间。

FP16的动态范围(5.96× 10−8 ~ 65504) 远于 FP32的动态范围(1.4×10-45 ~ 3.4×1038)，FP16的精度$2^{-11}$远粗于 FP32的精度$2^{-24}$。

使用半精度优势：
（1） 减少所需显存。FP16减少约一半的显存占用，可以训练更大的模型，或使用更大batch_size进行训练，更充分的利用资源；
（2）减少了CPU到GPU的数据传输量，拷贝时间可缩短到之前的一半，节省了数据传输时间；
（3）访存减半，降低了访存计算比；
（4）通信量减半，减少通信时间，使得通信时间更容易被隐藏；
（5）使用Volta GPU，可使用Tensor Core，提供相对于FP32 8倍的计算吞吐量，提高计算速度。

使用FP16表示/计算带来的主要问题

（1）溢出错误
（2）因精度不足而带来舍入错误：当a与b均用FP16表示时，a=1与b=0.0001相加时，其结果是错误的，因为a/b=10000> $2^{11}$，此时b会因尾数右移而变为0，导致结果出错。

当进行浮点数进行加减运算时，首先要使两个数的阶码相同，即小数点的位置对齐，这个过程称为对阶。在对阶时规定使小阶向大阶看齐，通过小阶的尾数算术右移来改变阶码。对阶过程中，由于FP16只有10位的尾数，当小阶的尾数右移超过11 位时，会导致该数变为0，即以FP16表示的数，如果当大数与小数的比率为大于$2^{11}$ 时，加减法运算结果会出错。而FP32有23位尾数，可表达的精度范围更广，可有效地避免该问题。

以上两种问题，在训练过程中，可能会导致训练中计算或更新有问题，影响模型精度，甚至无法收敛，因此需要使用混合精度训练，同时兼顾FP16的速度和FP32的稳定性。

精度选择

1. 操作f(x)满足f(x)>>x, 应在FP32下进行，例如Exp, Square, Log, Cross-entropy，因为这些操作可能会在前向或者反向计算时有结果溢出；
2. FP16对于某些计算是安全的，例如ReLU，Sigmoid，Tanh，可以直接在FP16的精度下进行计算；
3. Convolution, MatMul等操作在FP16下进行，这些操作在Volta GPU上，可以使用Tensor Core进行计算，进一步提高计算性能；
4. 大型的规约应在FP32下计算，因为累加很多FP16数值容易造成数据溢出；
5. Loss计算应在FP32中进行，因为Loss计算如Softmax, cross-entropy等操作中涉及到Exp, log等对FP16不安全的操作，使用FP16时可能会导致溢出。

训练

梯度更新
问题：梯度过小产生下溢导致梯度为0；学习率过小，而导致梯度与学习率的乘积过小产生下溢；权重相较于其更新值过大（ param/update>$2^{11}$），会因FP16精度不足，在对阶过程中使更新值变为0，导致不会更新权重。

所以需要保留FP32的权重，每次迭代时，制作这些权重的FP16副本并使用它们用于前向计算和反向计算，更新时将梯度再转换为FP32并用于更新FP32的权重。

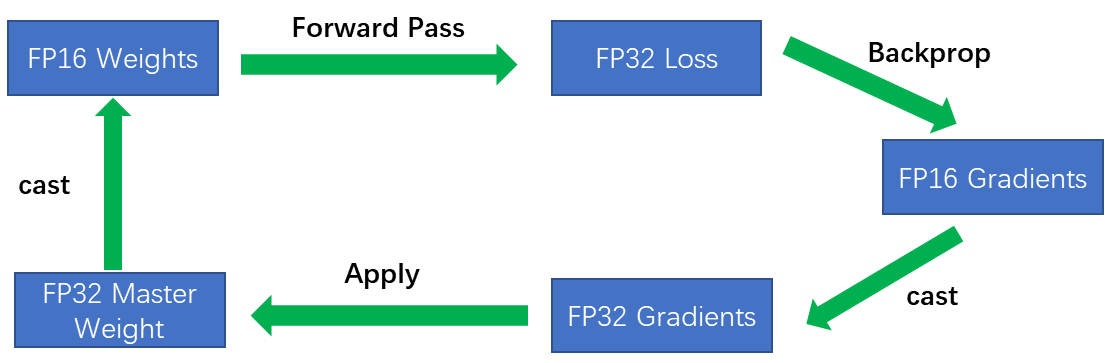
混合精度训练过程

1. 使用FP16的输入；
2. 前向计算：该场景中使用统一的FP32格式的初始化权重，训练时恢复checkpoint中的变量进行训练；将恢复的FP32参数转化为FP16供给前向运算；
3. Loss计算：该场景中loss计算复杂，涉及到许多exp, log等可能会发生FP16溢出的不稳定操作，因此loss计算在FP32精度下进行；
4. loss scale：将计算出来的loss乘以一个比例因子 scaled_loss = loss * loss_scale；
5. 反向计算：grads = tf.gradients(scaled_loss , params,aggregation_method=aggmeth)
6. 梯度计算完成后再将各梯度缩小相应的倍数：unscaled_grads = [(grad * (1. / loss_scale)) for grad in grads]；
7. 梯度规约：累加很多FP16数值容易造成数据溢出，选择在FP32下规约；
8. 参数更新：根据梯度是否溢出选择是否进行参数更新并动态调整 loss_scale，若更新，直接在FP32精度的参数上进行参数更新。由于该场景中就是使用PF32的参数，更新时直接应用于该参数即可。

为保证梯度落入半精度可表示范围内一个简单有效的方法将训练损失乘以比例因子，根据梯度的链式法则使得所有梯度也等比例放大。当然在权重更新之前，需要以相同的比例因子缩小梯度，再更新到权重上。即loss scale

注意：目前使用 bf16，有更大的表示范围，不需要 loss scale 了

megatron-3，节约激活值的显存

通过序列并行sequence parallelism 和选择性激活重算 selective activation recomputation。结合张量并行，这些技术几乎消除了重新计算激活的必要性。我们在规模达到一万亿个参数的语言模型上进行了评估，并展示了我们的方法可以将激活内存降低5倍，同时将激活重算的执行时间开销降低超过90%。

序列并行sequence parallelism

在transformer的非tensor并行区域中（即layer-norms 和 dropouts，这些操作是要将[b, s, h]复制到各个卡来执行），操作在序列维度s上是独立的。 这个特性允许我们沿着序列维度 s 划分这些区域[b, s/p, h]。 沿序列维度进行分区减少了激活所需的内存。

原MLP操作，其中AB是权重：
$$\begin{gathered} Y=LayerNorm(X), \\ Z=GeLU(YA), \\ W=ZB, \\ V=Dropout(W), \end{gathered}$$

加入序列并行后，MLP操作如下图所示：

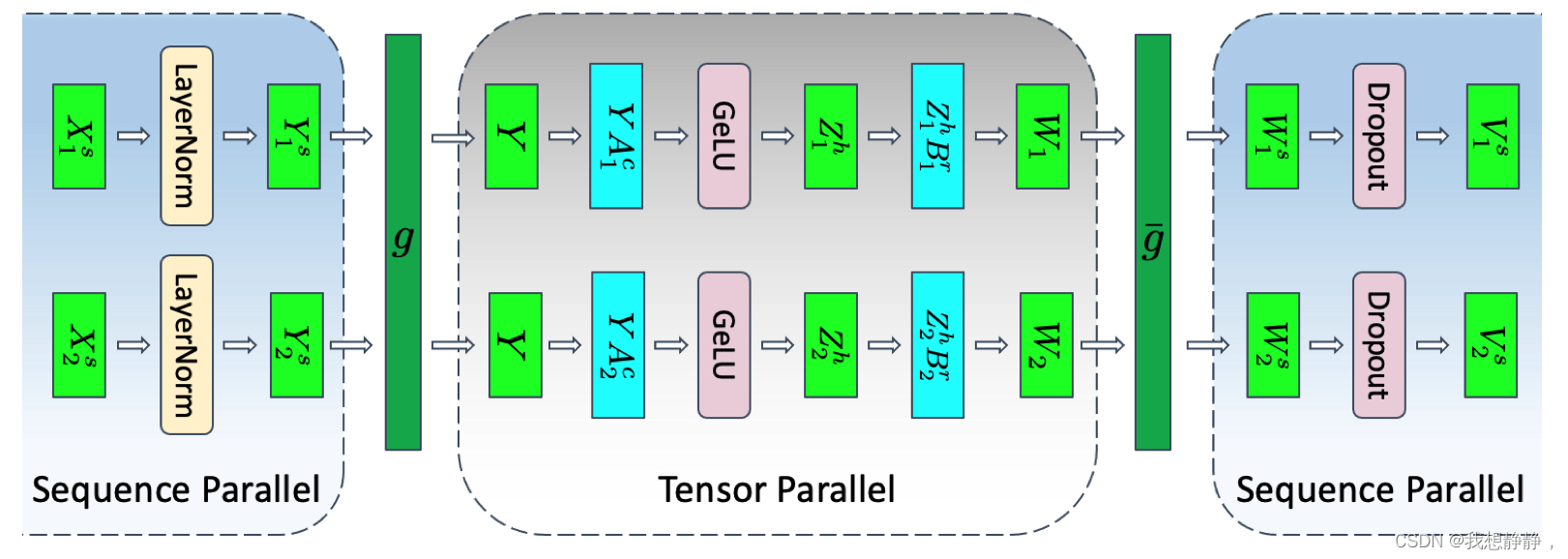
1. 将 X [b, s, h]划分到各个卡，即[b, s/p, h]
2. 各个卡并行计算$[b,s/p,h]=LayerNorm([b,s/p,h])$
3. GeLU(Y A)需要整个输入 Y，因此需要执行all-gather，得到完整Y [b, s, h]
4. A沿列切分为[h, 4h/p]，计算Z = GeLU(Y A) ，即 $[b,s,h]\times [h,4h/p]=[b,s,4h/p]$
5. B沿行切分为[4h/p, h]，计算W = ZB，即$[b,s,4h/p]\times [4h/p,h]=[b,s,h]$
6. 在megatron-LM中，需要对p个 [b, s, h]执行all-reduce在dropout，但是这里将dropout改成了序列并行，则需要对p个 [b, s, h]执行reduce-scatter，得到p个[b, s/p, h]，即各个卡上有W沿s维度的局部
7. 各个卡并行计算V =Dropout(W)，即$[b,s/p,h]=Dropout([b,s/p,h])$

self-attention同理，因此transformer layer如下图所示：

这里g是all-gather，g的共轭是reduce-scatter

在megatron中，transformer layer前向与后向计算时各有两个all-reduce操作，这里加入序列并行后，transformer layer前向与后向计算时各有两个all-gather和reduce-scatter操作。操作多了一倍，但是all-reduce = reduce-scatter + all-gather，因此通讯量不变，并行度增加。激活值所占显存减少。

激活值所占显存减少的原因，megatron-LM中的layer-norms 和 dropouts是要将输入复制到各个卡上，重复运算，也就是说激活值复制了p份，而使用序列并行化，可以仅仅保留一份激活值，而且是分布在各个gpu上。

选择性激活重算 selective activation recomputation

把Transformer族模型的所有activation消耗算了一遍，然后发现在Transformer核里有一些操作是产生的激活值又大，但是计算量又小的，这些激活值不保存，反向传播时重新计算。其他的激活值存下来，以节省重计算量。

比如下图的红框区域，具有很大的输入大小和很大的激活值，但每个输入元素的浮点运算（FLOPs）数量非常低。这部分需要重新计算而不是存下来

Checkpointing Skipping

在GPU的显存没占满的时候，可以不做checkpointing，这么一来重计算所带来的额外计算代价会进一步减小。

各种优化措施 与 激活值显存占用

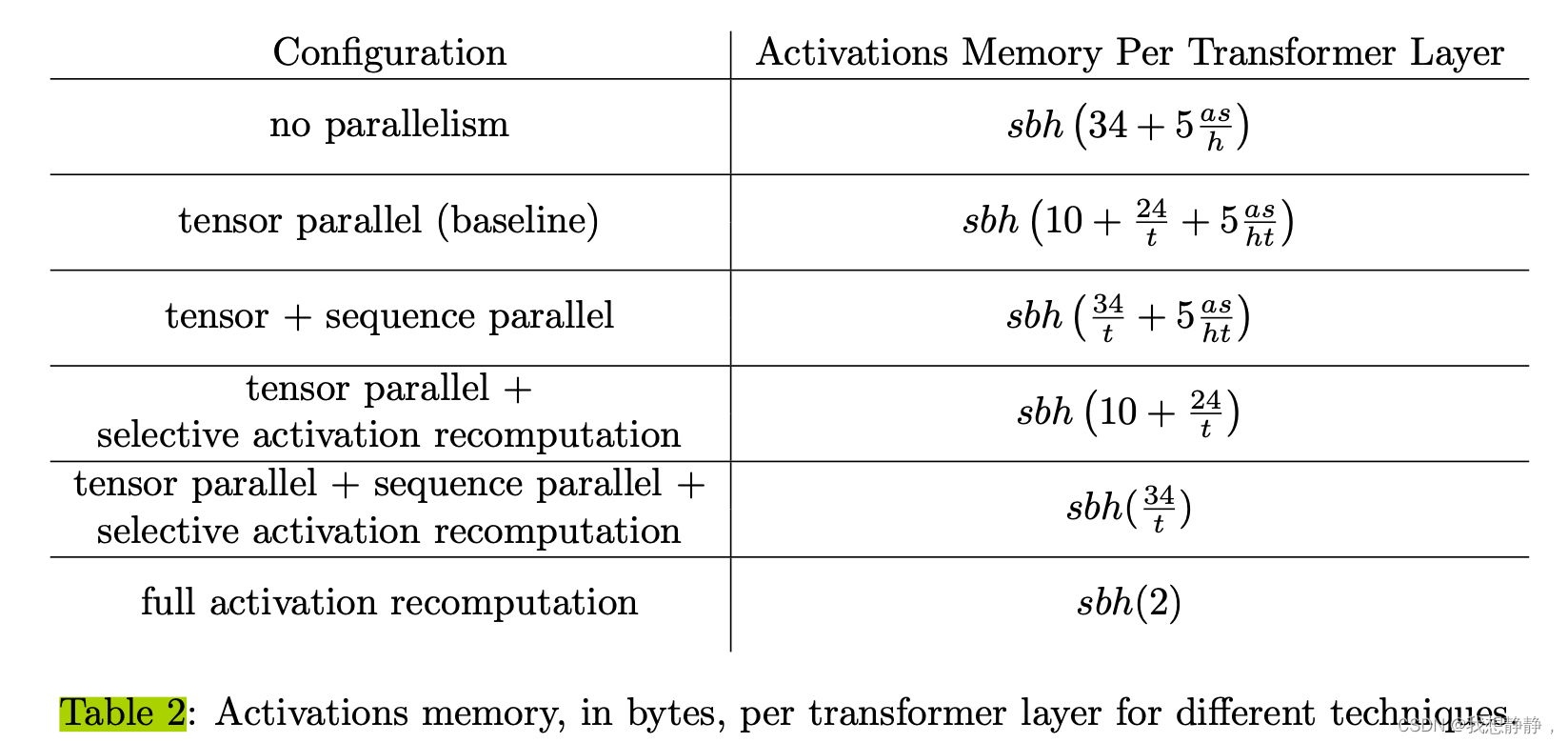
tensor parallel + sequence parallel + selective activation recomputation非常节省显存

https://zhuanlan.zhihu.com/p/614166245
https://zhuanlan.zhihu.com/p/498422407
https://zhuanlan.zhihu.com/p/343570325
https://zhuanlan.zhihu.com/p/513571706
https://zhuanlan.zhihu.com/p/617087561
https://zhuanlan.zhihu.com/p/68692579
https://arxiv.org/pdf/1909.08053.pdf
https://arxiv.org/pdf/2205.05198.pdf
https://zhuanlan.zhihu.com/p/628820408