【图】

在数据结构与算法09：二叉树这篇文章中讲述了“树”这种数据结构，如果把树中非父子关系的节点连接起来，就是一个“图”（Graph），如下所示，将树中的B和C节点连接起来就是一个图：

图中的元素叫作顶点（vertex）；
图中的一个顶点可以与任意其他顶点建立连接关系，这种关系叫作边（edge）；
跟顶点相连接的边的条数叫作顶点的度（degree）。

树和图的区别：

树表达的是层级化的结构，图表达的是网络化的结构。
树有一个根节点，下面的每一棵子树都有唯一的根节点；图的每一个节点都可以看作是平等的，并且节点与节点之间的连接也更为自由。
在树中一个父节点只能与它的子节点相连，但不会与孙子节点相连；图的任意节点都是可以相连的。

图的一个主要应用就是表示社交网络，比如微信中的每个用户可以看作一个顶点，如果两个用户是好友，那就在两者之间建立一条边，整个微信的好友关系就可以用一张图来表示。每个用户有多少个好友，在图中表示就是某个顶点有多少个度。如下所示：

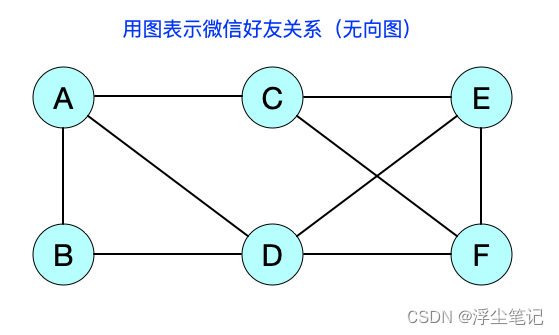
一共有6个用户，其中用户A的好友有B、C、D。用户A一共有3个好友。

另外还有微博的社交关系也可以用图来表示，但是更加复杂一点，因为微博允许单向关注，假设用户A关注了用户B，但用户B可以不关注用户A。用图表示这种单向的社交关系需要引入边的“方向”，如下所示：

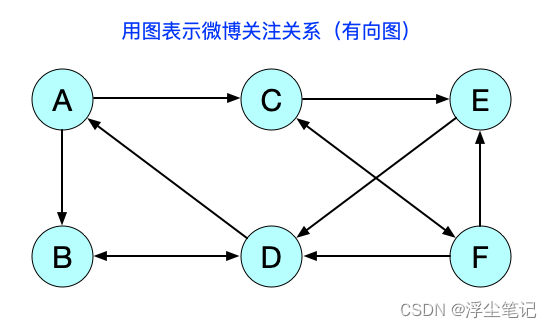
用户B和D互相关注，用户C和F互相关注，其它的都是单向关注。

对于边没有方向的图叫作“无向图”，边有方向的图叫作“有向图”。在有向图中，把度分为入度（In-degree）和出度（Out-degree）。

顶点的入度：表示有多少条边指向这个顶点，在微博中可以表示有多少粉丝；
顶点的出度：表示有多少条边是以这个顶点为起点指向其他顶点，在微博中表示关注了多少人。

另外还有一种图叫做带权图（weighted graph），每条边都有一个权重（weight），可以通过这个权重来表示好友间的亲密度。如下所示：

图在现实生活中的另一个重要应用就是地图交通网络，比如要规划一条双向车道，可以使用无向图；规划一条单向车道，可以使用有向图。其实无向图也可以认为是有向图的双向指向。

【图的存储方法】

方法1：邻接矩阵

邻接矩阵（Adjacency Matrix）：底层依赖一个二维数组，存储起来比较浪费空间，但是使用起来比较节省时间。（空间换时间）

对于无向图来说，如果顶点A与顶点B之间有边，就将 array[A][B] 和 array[B][A] 标记为 1；
对于有向图来说，如果有一条箭头从顶点A指向顶点B，就将 array[A][B] 标记为 1；如果有一条箭头从顶点B指向顶点A，就将 array[B][A] 标记为 1；
对于带权图，数组中就存储相应的权重。

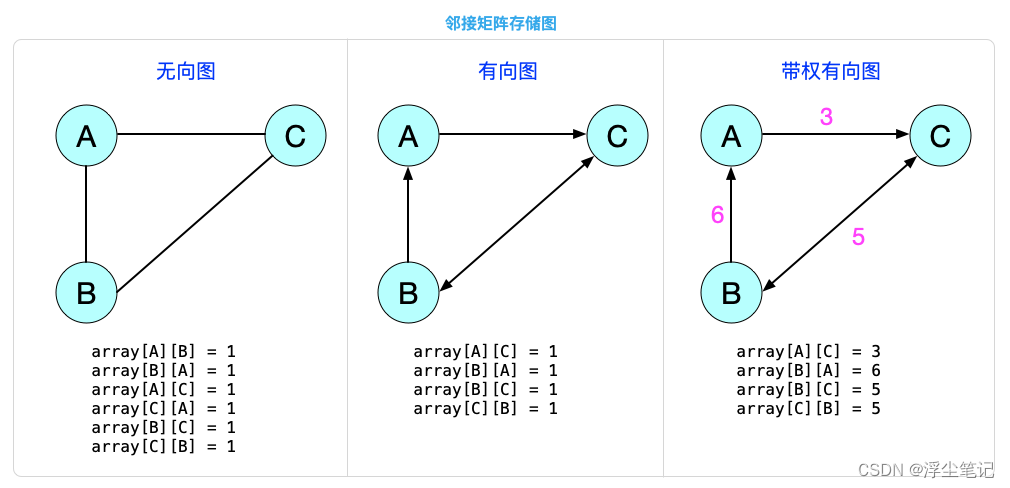
对于无向图来说，array[A][B] = 1 和 array[B][A] = 1 其实只需要存储一个就可以了，所以使用邻接矩阵表示一个图会比较浪费存储空间。

还有一种图是 稀疏图（Sparse Matrix），顶点很多但每个顶点的边并不多，如果使用邻接矩阵的存储方法就更加浪费空间了。如下所示：

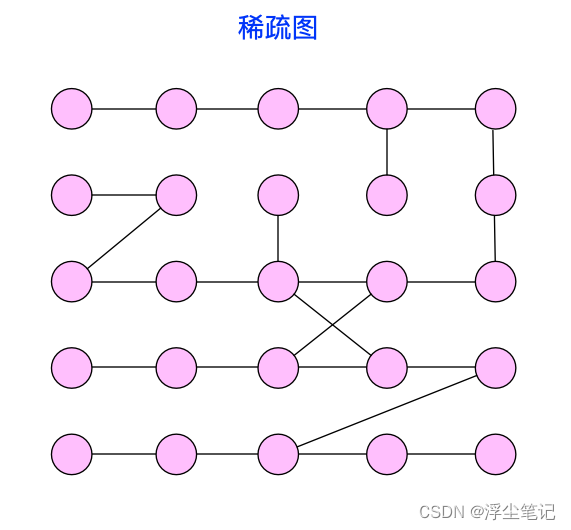
比如微信有好几亿的用户，对应到图上就是好几亿的顶点，但是每个用户的好友并不会很多，一般也就三五百个而已。如果用邻接矩阵来存储，那么绝大部分的存储空间都被浪费了。

方法2：邻接链表

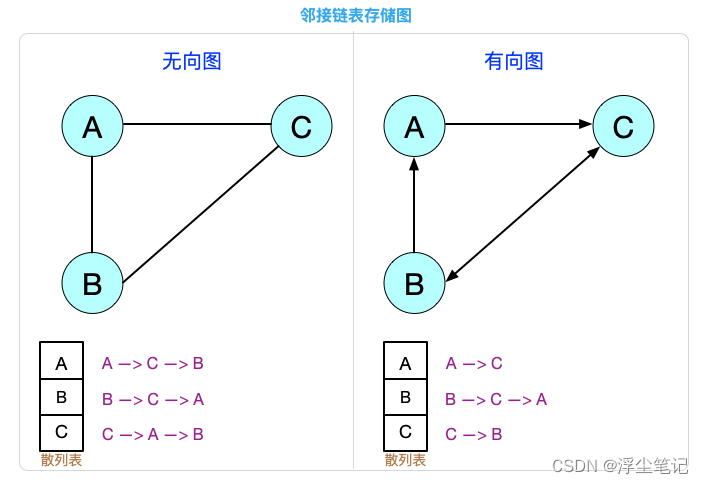
邻接链表（Adjacency List）：底层依赖一个链表，存储起来比较节省空间，但是使用起来比较耗时间。（时间换空间）

这种存储方式有点类似散列表，每个顶点对应一条链表，链表中存储的是与这个顶点相连接的其他顶点；
对于有向图的邻接链表存储方式，每个顶点对应的链表里面存储的是指向的顶点；
对于无向图的邻接链表存储方式，每个顶点的链表中存储的是跟这个顶点有边相连的顶点。

【图的算法】

图的算法一般分为广度优先搜索（BFS）和深度优先搜索（DFS），主要实现在图中从一个顶点出发到另一个顶点的路径。

广度优先搜索（BFS）

广度优先搜索（Breadth-First-Search，简称为 BFS），是一种“地毯式”层层推进的搜索策略，即先查找离起始顶点最近的，然后依次往外搜索。如下所示：

举个例子：当你去一个地方旅游，进入景区后漫无目的的游览，会有很多条可以游览的路线，如果从起点出发，由近到远的溜达一遍，不走回头路。这个过程就可以理解为广度优先。

使用Go代码实现广度优先搜索如下：

// go-algo-demo/graph/Graph.go
package main

import (
	"container/list"
	"fmt"
)

// 使用邻接链表存储无向图
type Graph struct {
	data  []*list.List
	value int
}

// 根据设定的容量初始化一个图
func newGraph(v int) *Graph {
	graph := &Graph{
		data:  make([]*list.List, v),
		value: v,
	}
	for i := range graph.data {
		graph.data[i] = list.New()
	}
	return graph
}

// 给图添加边,每条边都添加进去
func (self *Graph) addEdge(start int, end int) {
	//无向图的一条边需要添加两次
	self.data[start].PushBack(end)
	self.data[end].PushBack(start)
}

// 广度优先搜索:start起始点,end结束点
// 搜索一条从start到end的最短路径
func (self *Graph) BFS(start int, end int) {
	if start == end {
		return
	}

	//visited记录已经被访问的顶点
	visited := make([]bool, self.value)
	visited[start] = true

	//queue是一个队列，用来存储已经被访问、但相连的顶点还没有被访问的顶点
	var queue []int
	queue = append(queue, start)

	//path用来记录搜索路径,从顶点start开始，广度优先搜索到顶点end后，path数组中存储的就是搜索的路径
	path := make([]int, self.value)
	for index := range path {
		path[index] = -1
	}

	//标记是否已找到
	isFound := false
	for len(queue) > 0 && !isFound {
		top := queue[0]
		queue = queue[1:]
		linkedlist := self.data[top]
		for e := linkedlist.Front(); e != nil; e = e.Next() {
			k := e.Value.(int)
			if !visited[k] {
				path[k] = top
				if k == end {
					isFound = true
					break
				}
				queue = append(queue, k)
				visited[k] = true
			}
		}
	}
	if isFound {
		printPath(path, start, end)
	} else {
		fmt.Printf("从 %d 到 %d 的路径没有找到\n", start, end)
	}
}

// 递归打印路径
func printPath(path []int, s int, t int) {
	if t == s || path[t] == -1 {
		fmt.Printf("%d ", t)
	} else {
		printPath(path, s, path[t])
		fmt.Printf("%d ", t)
	}
}

func main() {
	graph := newGraph(8)
	//把图的所有边都添加进去
	graph.addEdge(0, 1)
	graph.addEdge(1, 2)
	graph.addEdge(0, 3)
	graph.addEdge(1, 4)
	graph.addEdge(3, 4)
	graph.addEdge(4, 5)
	graph.addEdge(2, 5)
	graph.addEdge(5, 7)
	graph.addEdge(4, 6)
	graph.addEdge(6, 7)

	//广度优先搜索从0到6的路径
	graph.BFS(0, 6) //0 1 4 6

	//广度优先搜索从3到7的路径
	graph.BFS(3, 7) //3 4 5 7
}

代码说明：

visited记录的是已经被访问的顶点，避免顶点被重复访问。如果顶点 q 被访问，那相应的 visited[q] 设置为 true。
queue是一个队列，用来存储已经被访问、但相连的顶点还没有被访问的顶点。因为广度优先搜索是逐层访问的，只有把第 k 层的顶点都访问完成之后，才能访问第 k+1 层的顶点。当访问到第 k 层顶点的时候，需要把第 k 层的顶点记录下来，稍后才能通过第 k 层的顶点来找第 k+1 层的顶点。
path用来记录搜索路径,从顶点start开始，广度优先搜索到顶点end后，path数组中存储的就是搜索的路径。不过，这个路径是反向存储的, path[x] 存储的是顶点x是从哪个前驱顶点遍历过来的。比如，通过顶点2的邻接表访问到顶点3，那 path[3] 就等于2。为了正向打印出路径，需要递归地打印，可以看下 printPath() 函数的实现方式。

复杂度分析：

假设 V 表示顶点的个数，E 表示边的个数。
最坏情况下，结束点end距离起始点start很远，需要遍历完整个图才能找到。这个时候，每个顶点都要进出一遍队列，每个边也都会被访问一次，所以广度优先搜索的时间复杂度是 O(V+E)。如果一个图中的所有顶点都是连通的，E 肯定要大于等于 V-1。所以，广度优先搜索的时间复杂度是 O(E)。
广度优先搜索的空间消耗主要在变量 visited 数组、queue 队列、path 数组上，这三个存储空间的大小都不会超过顶点的个数，所以广度优先搜索的空间复杂度是 O(V)。

深度优先搜索（DFS）

深度优先搜索（Depth-First-Search，简称为 DFS），从起始顶点出发随意选一条路走下去，如果发现路不通，又得原路返回到上一个岔路口重新找下一条路线，类似于“走迷宫”的场景。如下所示：

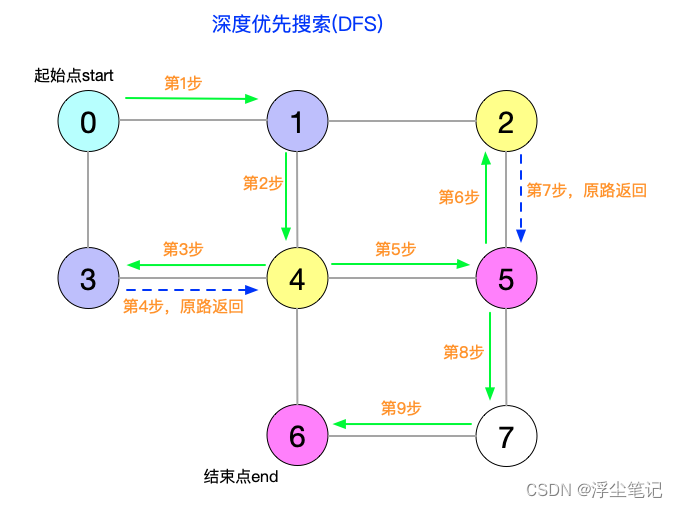
举个例子：当你去一个地方旅游，进入景区后不想瞎溜达，只想奔着一个目的地，需要从起点出发找一条路试试，如果这条路不能到达目的地，需要原路返回到上一个岔路口重新选择新的路线。这个过程就可以理解为深度优先。深度优先搜索用的是 回溯思想，适合用递归来实现。

使用Go代码实现深度优先搜索如下：

// 广度优先搜索:start起始点,end结束点
func (self *Graph) DFS(start int, end int) {
	path := make([]int, self.value)
	for i := range path {
		path[i] = -1
	}
	visited := make([]bool, self.value)
	visited[start] = true

	isFound := false
	self.DFSRecurse(start, end, path, visited, isFound)
	printPath(path, start, end)
}

// 广度优先:递归搜索路径
func (self *Graph) DFSRecurse(start int, end int, path []int, visited []bool, isFound bool) {
	if isFound {
		return
	}
	visited[start] = true
	if start == end {
		isFound = true
		return
	}
	linkedlist := self.data[start]
	for e := linkedlist.Front(); e != nil; e = e.Next() {
		k := e.Value.(int)
		if !visited[k] {
			path[k] = start
			self.DFSRecurse(k, end, path, visited, false)
		}
	}
}

func main() {
	graph := newGraph(8)
	//把图的所有边都添加进去
	graph.addEdge(0, 1)
	graph.addEdge(1, 2)
	graph.addEdge(0, 3)
	graph.addEdge(1, 4)
	graph.addEdge(3, 4)
	graph.addEdge(4, 5)
	graph.addEdge(2, 5)
	graph.addEdge(5, 7)
	graph.addEdge(4, 6)
	graph.addEdge(6, 7)

	//深度优先搜索从0到6的路径
	graph.DFS(0, 6) //0 1 2 5 4 6

	//深度优先搜索从3到7的路径
	graph.DFS(3, 7) //3 0 1 2 5 4 6 7
}

复杂度分析：

假设 V 表示顶点的个数，E 表示边的个数。

每条边最多会被访问两次，一次是遍历，一次是回退。所以，深度优先搜索算法的时间复杂度是 O(E)。

深度优先搜索算法的消耗内存主要是 visited、path 数组和递归调用栈，visited、path 数组的大小跟顶点的个数 V 成正比，递归调用栈的最大深度不会超过顶点的个数，所以深度优先算法的空间复杂度是 O(V)。

总结：广度优先搜索需要使用队列来实现，遍历得到的路径就是起始顶点到终止顶点的最短路径；深度优先搜索用的是回溯思想，适合用递归实现，可以使用栈来实现的。深度优先和广度优先的时间复杂度都是 O(边的个数)，空间复杂度是 O(顶点的个数)。