VolSDF(neurips 2021)

题目：Volume Rendering of Neural Implicit Surfaces
链接：https://arxiv.org/pdf/2106.12052.pdf
目标：使用SDF这种表示方式替换NeRF中的MLP，使得在几何形状上获得更准确的结果。我们通过将体密度建模为几何形状的函数来实现这一点（We achieve that by modeling the volume density as a function of the geometry.）。

方法：1. 将体密度利用公式转为可学习的SDF，使得

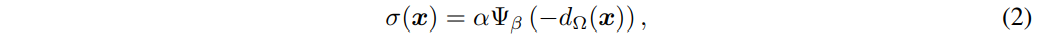
alpha和beta是可学习的参数。其余看不懂。
总之，文章的核心应该在于 解耦颜色和几何信息的优化，从而可以将desity表示为SDF进行优化，以及实现一系列其他目的，比如：分离颜色和几何。
This provides a useful inductive bias for disentangling density and radiance fields, which in turn provides a more accurate geometry approximation.

inductive bias

这里出现了一个高频词——inductive bias（归纳偏差），通俗理解：从现实生活中观察到的现象中归纳出一定的规则，然后对模型做一定的约束，从而可以起到 “模型选择” 的作用，类似贝叶斯学习中的 “先验”。
原文中写道： it provides a useful inductive bias for the surface geometry. 我理解的这句话等价于 我们的方法可以直接优化几何（也就是desity），怎么能写得这么高级呢？？