参考资料
Fleiss Kappa的定义
Fleiss Kappa的原论文因为要付费才能阅读，我这里就不放链接了
Fleiss' kappa - Wikipedia
https://en.wikipedia.org/wiki/Fleiss%27_kappa
Fleiss Kappa相关统计量 Z值，p值，95%置信区间
属性一致性分析 的 kappa 统计量的方法和公式 - Minitab请选择您所选的方法或公式。
https://kns.cnki.net/kcms2/article/abstract?v=30M9_8jKqe0eeyUFGF2Hn7wI0LSs-Y73fT2Qnj25ZztRFGn-k7w38HpuuprNL7uDobRQegHTkIu0rsYpWZAWQXSLhgCo5vf_lwfoH8muLibc8UPwv_ZzuvwiTEcRGaXb&uniplatform=NZKPT&language=CHSFleiss' kappa in SPSS Statistics | Laerd Statisticshttps://statistics.laerd.com/spss-tutorials/fleiss-kappa-in-spss-statistics.php
第一个和第二个链接提供了计算公式，第三个链接是SPSS的计算Fleiss Kappa的图文教程，没有涉及公式推理。
前情提要
网上关于Fleiss Kappa的资料比较多，但是相关统计量，如Z值和P值的资料比较少。维基百科只提供了Fleiss Kappa的计算方法，没有提及相关统计量的计算。
期间找了很多工具，如SPSS，Minitab和SPSSAU。SPSS和Minitab是付费软件，SPSSAU是免费的在线分析平台。但SPSSAU只允许5万条及以下的数据进行分析，而我的数据量超过了5万条。
找遍全网好像没有人公开计算Fleiss Kappa相关统计量的代码，而可以计算这些统计量的软件要么是付费的，要么是存在数据量的限制，我就想能不能自己实现一个计算工具。
Fleiss Kappa原理
关于Fleiss Kappa的原理部分，我觉得还是看维基百科比较好，他写的比较清楚，还提供了数据示例。下面是关于Fleiss Kappa的计算代码。
import numpy as np
def fleiss_kappa(data: np.array):
"""
Calculates Fleiss' kappa coefficient for inter-rater agreement.
Args:
data: numpy array of shape (subjects, categories), where each element represents
the number of raters who assigned a particular category to a subject.
Returns:
kappa: Fleiss' kappa coefficient.
"""
subjects, categories = data.shape
n_rater = np.sum(data[0])
p_j = np.sum(data, axis=0) / (n_rater * subjects)
P_e_bar = np.sum(p_j ** 2)
P_i = (np.sum(data ** 2, axis=1) - n_rater) / (n_rater * (n_rater - 1))
P_bar = np.mean(P_i)
K = (P_bar - P_e_bar) / (1 - P_e_bar)subjects是样本数量，相当于维基百科中的N
categories是类别数量，相当于维基百科中的k
n_rater是投票者的数量，相当于维基百科中的n
data是输入的矩阵，第i行j列的元素是维基百科中的
这里我提供维基百科的公式截图，可以对照看一下
相关统计量的计算
下图是Minitab提供的公式，链接我放在了博客开头
z值算出来后，p-value和95%置信区间就水到渠成了。
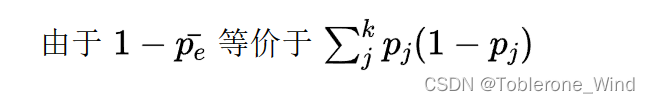
在代码中我使用tmp进行了替换，简化了表达式
tmp = (1 - P_e_bar) ** 2
var = 2 * (tmp - np.sum(p_j * (1 - p_j) * (1 - 2 * p_j))) / (tmp * subjects * n_rater * (n_rater - 1))
# standard error
SE = np.sqrt(var)
Z = K / SE
p_value = 2 * (1 - norm.cdf(np.abs(Z)))
ci_bound = 1.96 * SE / subjects
lower_ci_bound = K - ci_bound
upper_ci_bound = K + ci_bound下面是完整代码
import numpy as np
from scipy.stats import norm
def fleiss_kappa(data: np.array):
"""
Calculates Fleiss' kappa coefficient for inter-rater agreement.
Args:
data: numpy array of shape (subjects, categories), where each element represents
the number of raters who assigned a particular category to a subject.
Returns:
kappa: Fleiss' kappa coefficient.
"""
subjects, categories = data.shape
n_rater = np.sum(data[0])
p_j = np.sum(data, axis=0) / (n_rater * subjects)
P_e_bar = np.sum(p_j ** 2)
P_i = (np.sum(data ** 2, axis=1) - n_rater) / (n_rater * (n_rater - 1))
P_bar = np.mean(P_i)
K = (P_bar - P_e_bar) / (1 - P_e_bar)
tmp = (1 - P_e_bar) ** 2
var = 2 * (tmp - np.sum(p_j * (1 - p_j) * (1 - 2 * p_j))) / (tmp * subjects * n_rater * (n_rater - 1))
# standard error
SE = np.sqrt(var)
Z = K / SE
p_value = 2 * (1 - norm.cdf(np.abs(Z)))
ci_bound = 1.96 * SE / subjects
lower_ci_bound = K - ci_bound
upper_ci_bound = K + ci_bound
print("Fleiss Kappa: {:.3f}".format(K))
print("Standard Error: {:.3f}".format(SE))
print("Z: {:.3f}".format(Z))
print("p-value: {:.3f}".format(p_value))
print("Lower 95% CI Bound: {:.3f}".format(lower_ci_bound))
print("Upper 95% CI Bound: {:.3f}".format(upper_ci_bound))
print()这个函数只能处理格式形如维基百科示例的数据，对于其他格式的数据，需要相关的转换函数。
这里提供了两个转换函数，和对应的测试数据
def transform(*raters):
"""
Transforms the ratings of multiple raters into the required data format for Fleiss' Kappa calculation.
Args:
*raters: Multiple raters' ratings. Each rater's ratings should be a list or array of annotations.
Returns:
data: numpy array of shape (subjects, categories), where each element represents the number of raters
who assigned a particular category to a subject.
"""
assert all(len(rater) == len(raters[0]) for rater in raters), "Lengths of raters are not consistent."
subjects = len(raters[0])
categories = max(max(rater) for rater in raters) + 1
data = np.zeros((subjects, categories))
for i in range(subjects):
for rater in raters:
data[i, rater[i]] += 1
return data
def tranform2(weighted):
"""
Transforms weighted data into the required data format for Fleiss' Kappa calculation.
Args:
weighted: List of weighted ratings. Each row represents [rater_0_category, rater_1_category, ..., rater_n_category, weight].
Returns:
data: numpy array of shape (subjects, categories), where each element represents the number of raters
who assigned a particular category to a subject.
"""
n_rater = len(weighted[0]) - 1
raters = [[] for _ in range(n_rater)]
for i in range(len(weighted)):
for j in range(len(raters)):
raters[j] = raters[j] + [weighted[i][j] for _ in range(weighted[i][n_rater])]
data = transform(*raters)
return data
def test():
# Example data provided by wikipedia https://en.wikipedia.org/wiki/Fleiss_kappa
data = np.array([
[0, 0, 0, 0, 14],
[0, 2, 6, 4, 2],
[0, 0, 3, 5, 6],
[0, 3, 9, 2, 0],
[2, 2, 8, 1, 1],
[7, 7, 0, 0, 0],
[3, 2, 6, 3, 0],
[2, 5, 3, 2, 2],
[6, 5, 2, 1, 0],
[0, 2, 2, 3, 7]
])
fleiss_kappa(data)
# need transform
rater1 = [1, 2, 2, 1, 2, 2, 1, 1, 3, 1, 2, 2]
rater2 = [1, 2, 1, 2, 1, 2, 3, 2, 3, 2, 3, 1]
rater3 = [1, 2, 2, 1, 3, 3, 3, 2, 1, 2, 3, 1]
data = transform(rater1, rater2, rater3)
fleiss_kappa(data)
# The first row indicates that both rater 1 and 2 rated as category 0, this case occurs 8 times.
# need transform2
weighted_data = [
[0, 0, 8],
[0, 1, 2],
[0, 2, 0],
[1, 0, 0],
[1, 1, 17],
[1, 2, 3],
[2, 0, 0],
[2, 1, 5],
[2, 2, 15]
]
data = tranform2(weighted_data)
fleiss_kappa(data)
test()代码准确性
对于测试的3个数据，我同时使用了SPSSAU和SPSS进行统计分析，它们的结果和我代码计算结果一致。
对于我自身的42万条数据，使用SPSS和我代码计算的结果一致。
代码和测试数据已上传到github，欢迎下载和打星
Fleiss-Kappa/ at main · Lucienxhh/Fleiss-Kappa · GitHubhttps://github.com/Lucienxhh/Fleiss-Kappa
