👻内容专栏:《数据结构与算法篇》
🐨本文概括: 继上一篇深入浅出_二叉树之后遗漏掉了,再次写一篇二叉树的性质博文,对二叉树进行补充总结。
🐼本文作者:花 碟
🐸发布时间:2023.6.8
二叉树的性质
对于二叉树,有以下几条性质:
- 若规定根节点的层数为1,则一棵非空二叉树的第
i层上最多有2^(i - 1)个结点- 若规定根节点的层数为1,则深度为
h的二叉树的最大结点数是2^h - 1- 对任何一棵二叉树, 如果度为0其叶结点个数为
n₀, 度为2的分支结点个数为n₂,则有n₀=n₂ +1- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,
h=log₂(n + 1). (ps:log₂(n + 1) 是log以2为底,n+1为对数)
🏃♂️🏃♂️牛刀小试:
-
- 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A. 不存在这样的二叉树
B. 200
C. 198
D. 199
解释:我们直接套用上面的第3条性质,度为2的分支结点个数为199, 那么度为0的分支结点个数比度为2的分支节点个数多一个,199 + 1 = 200
- 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
-
- 下列数据结构中,不适合采用顺序存储结构的是( )
A. 非完全二叉树
B. 堆
C. 队列
D. 栈
解释:堆一般为二叉树的顺序存储结构,所以适合,栈遵循后进先出的原则,也适合,对于队列和非完全二叉树来说,队列相对来说,更易于用顺序存储,比如说循环队列,但是非完全二叉树就不适合了,因为可能存在很多空树的情况,导致空间出现大量的浪费,所以不适合。
- 下列数据结构中,不适合采用顺序存储结构的是( )
-
- 在具有 2n 个节点的完全二叉树中,叶子节点个数为( )
A. n
B. n+1
C. n-1
D. n/2
解释:对于一个完全二叉树节点个数为2n,设叶子节点的个数为n₀,度为1的节点个数为n₁,度为2的节点个数为n₂,则必有n₀+ n₁ + n₂ = 2n,而完全二叉树度为1的节点只有0个或者1个,这取决于完全二叉树最底层的节点的个数是奇数还是偶数,是奇数,n₁ 就为1;是偶数,n₁就为0。最后根据第3条的性质,代入进去,2n₀ - 1 + n₁ = 2n ,所以这里的n₁ 只能为1个,得到选项的结果,叶子节点个数就是n
- 在具有 2n 个节点的完全二叉树中,叶子节点个数为( )
-
- 一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
解释:2¹⁰是1024,2⁹是512, 高度为h的完全二叉树的最大节点数为2h - 1 + 1,高度为9的完全二叉树的最大节点数为 2⁹ - 1 + 1 = 512,高度为10的完全二叉树的最大节点数为 2¹⁰ - 1 + 1 = 1024,题目说是节点数为531个,小于高度为10的最大节点数。符合。
- 一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
-
- 一个具有767个节点的完全二叉树,其叶子节点个数为()
A. 383
B. 384
C. 385
D. 386
解释:这题与第三题类似,对于一个完全二叉树节点个数为767,设叶子节点的个数为n₀,度为1的节点个数为n₁,度为2的节点个数为n₂,则必有n₀+ n₁ + n₂ = 767,最后根据第3条的性质,代入进去,2n₀ - 1 + n₁ = 767,根据选项的结果,n₁为0,即完全二叉树最底层的节点个数为偶数,算得叶子节点个数为384
- 一个具有767个节点的完全二叉树,其叶子节点个数为()
根据两种遍历方式确定一颗二叉树
-
- 某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为( )
A. ABDHECFG
B. ABCDEFGH
C. HDBEAFCG
D. HDEBFGCA
解释: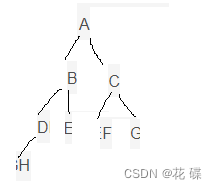
我们直接根据层序遍历的序列,把二叉树画出来,前序序列就很直观的写出来了。
- 某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为( )
-
- 二叉树的先序遍历和中序遍历如下:前序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A. E
B. F
C. G
D. H
解释:前序遍历的第一个节点即为根节点。
- 二叉树的先序遍历和中序遍历如下:前序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
-
- 设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为____。
A. adbce
B. decab
C. debac
D. abcde
解释:见下图
法一:前(or 后)序遍历确定根,中序遍历确定左右子树的区间。
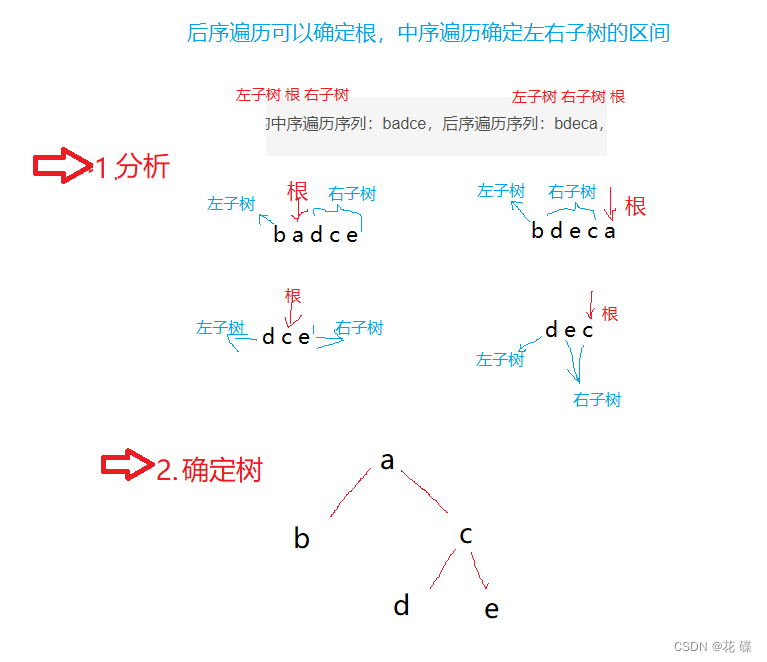
法二:第二种是投机取巧的方法,仅限于解题。将后序(or 前序)遍历的序列放置纵轴,且需要保证根的方向,按根的方向排列。然后将中序遍历的序列放置于横轴,确立两个相同的点的坐标,然后连线。
⚠ 注意连线的规则:①左子树的所有节点在父节点的左侧,右子树的所有节点在父节点的右侧。
②如果需要代码实现,还是第一种方法的思想适合写递归操作。
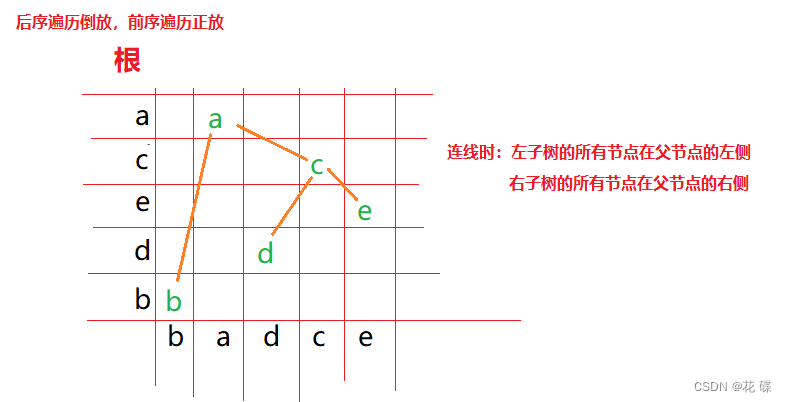
- 设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为____。
-
- 某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列
为
A. FEDCBA
B. CBAFED
C. DEFCBA
D. ABCDEF
解释:如下图
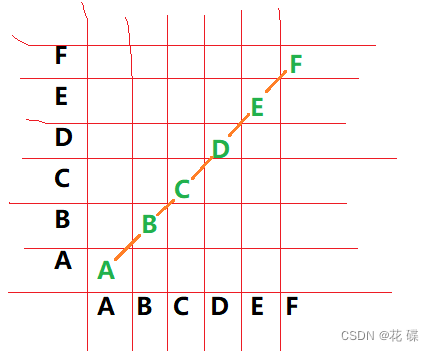
- 某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列
-
- 已知某二叉树的中序遍历序列为JGDHKBAELIMCF,后序遍历序列为JGKHDBLMIEFCA,则其前序遍历序列为( )
A.ABDGHJKCEFILM
B.ABDGJHKCEILMF
C.ABDHKGJCEILMF
D.ABDGJHKCEIMLF
解释:
法一: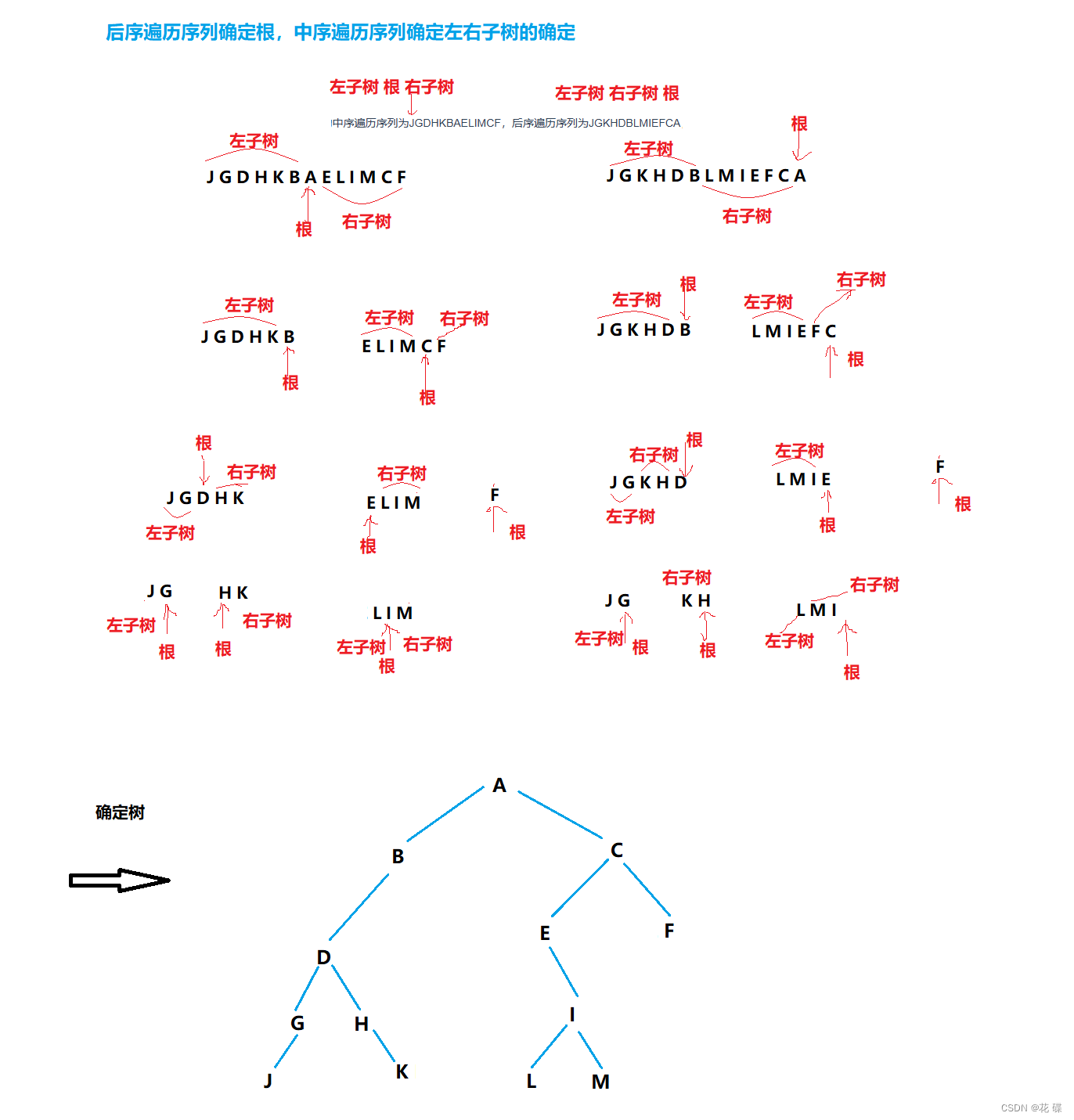
法二:
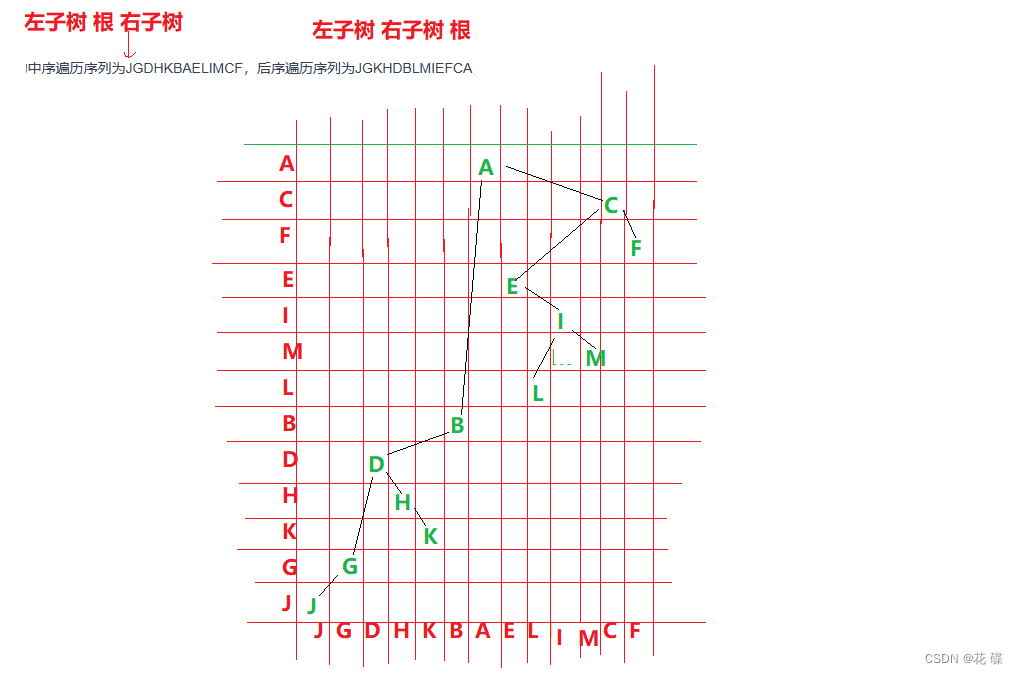
- 已知某二叉树的中序遍历序列为JGDHKBAELIMCF,后序遍历序列为JGKHDBLMIEFCA,则其前序遍历序列为( )
-
- 已知某二叉树的前序遍历序列为5 7 4 9 6 2 1,中序遍历序列为4 7 5 6 9 1 2,则其后序遍历序列为( )
A.4 2 5 7 6 9 1
B.4 2 7 5 6 9 1
C.4 7 6 1 2 9 5
D.4 7 2 9 5 6 1
解释:
通过前序遍历找到子树的根,在中序遍历中找到根的位置,然后确定根左右子树的区间,即根的左侧为左子树中所有节点,根的右侧为右子树中所有节点。
故:根为: 5
5的左子树:4 7 5的右子树: 6 9 1 2
5的左子树的根为: 7 5的右子树的根为:9
7的左子树: 4 7的右:空 9的左子树:6 9的右子树:2
确定树的结构为:
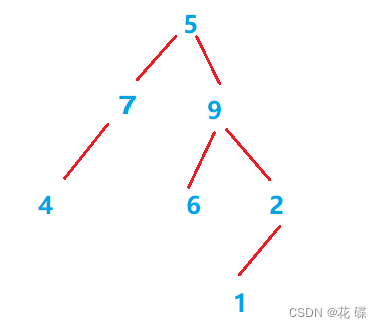
- 已知某二叉树的前序遍历序列为5 7 4 9 6 2 1,中序遍历序列为4 7 5 6 9 1 2,则其后序遍历序列为( )
🥰🥰本章节完,后续会补充二叉树进阶内容知识,小伙伴们可以持续关注,若本篇文章对你有帮助的话,可以三连支持博主哦~,另外本篇内容有编写有误的话,可以私聊博主进行纠正!