你有一辆货运卡车，你需要用这一辆车把一些箱子从仓库运送到码头。这辆卡车每次运输有 箱子数目的限制 和 总重量的限制 。

给你一个箱子数组 boxes 和三个整数 portsCount, maxBoxes 和 maxWeight ，其中 boxes[i] = [ports​​i​, weighti] 。

    ports​​i 表示第 i 个箱子需要送达的码头， weightsi 是第 i 个箱子的重量。
    portsCount 是码头的数目。
    maxBoxes 和 maxWeight 分别是卡车每趟运输箱子数目和重量的限制。

箱子需要按照 数组顺序 运输，同时每次运输需要遵循以下步骤：

    卡车从 boxes 队列中按顺序取出若干个箱子，但不能违反 maxBoxes 和 maxWeight 限制。
    对于在卡车上的箱子，我们需要 按顺序 处理它们，卡车会通过 一趟行程 将最前面的箱子送到目的地码头并卸货。如果卡车已经在对应的码头，那么不需要 额外行程 ，箱子也会立马被卸货。
    卡车上所有箱子都被卸货后，卡车需要 一趟行程 回到仓库，从箱子队列里再取出一些箱子。

卡车在将所有箱子运输并卸货后，最后必须回到仓库。

请你返回将所有箱子送到相应码头的 最少行程 次数。

 

示例 1：

输入：boxes = [[1,1],[2,1],[1,1]], portsCount = 2, maxBoxes = 3, maxWeight = 3
输出：4
解释：最优策略如下：
- 卡车将所有箱子装上车，到达码头 1 ，然后去码头 2 ，然后再回到码头 1 ，最后回到仓库，总共需要 4 趟行程。
所以总行程数为 4 。
注意到第一个和第三个箱子不能同时被卸货，因为箱子需要按顺序处理（也就是第二个箱子需要先被送到码头 2 ，然后才能处理第三个箱子）。

示例 2：

输入：boxes = [[1,2],[3,3],[3,1],[3,1],[2,4]], portsCount = 3, maxBoxes = 3, maxWeight = 6
输出：6
解释：最优策略如下：
- 卡车首先运输第一个箱子，到达码头 1 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第二、第三、第四个箱子，到达码头 3 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第五个箱子，到达码头 3 ，回到仓库，总共 2 趟行程。
总行程数为 2 + 2 + 2 = 6 。

示例 3：

输入：boxes = [[1,4],[1,2],[2,1],[2,1],[3,2],[3,4]], portsCount = 3, maxBoxes = 6, maxWeight = 7
输出：6
解释：最优策略如下：
- 卡车运输第一和第二个箱子，到达码头 1 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第三和第四个箱子，到达码头 2 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第五和第六个箱子，到达码头 3 ，然后回到仓库，总共 2 趟行程。
总行程数为 2 + 2 + 2 = 6 。

示例 4：

输入：boxes = [[2,4],[2,5],[3,1],[3,2],[3,7],[3,1],[4,4],[1,3],[5,2]], portsCount = 5, maxBoxes = 5, maxWeight = 7
输出：14
解释：最优策略如下：
- 卡车运输第一个箱子，到达码头 2 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第二个箱子，到达码头 2 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第三和第四个箱子，到达码头 3 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第五个箱子，到达码头 3 ，然后回到仓库，总共 2 趟行程。
- 卡车运输第六和第七个箱子，到达码头 3 ，然后去码头 4 ，然后回到仓库，总共 3 趟行程。
- 卡车运输第八和第九个箱子，到达码头 1 ，然后去码头 5 ，然后回到仓库，总共 3 趟行程。
总行程数为 2 + 2 + 2 + 2 + 3 + 3 = 14 。

 

提示：

    1 <= boxes.length <= 105
    1 <= portsCount, maxBoxes, maxWeight <= 105
    1 <= ports​​i <= portsCount
    1 <= weightsi <= maxWeight

解法一： 朴素版本

通过题目发现，我们可以很简单的抽象出一个集合状态,$dp[i]$即运送前i个箱子需要的最小行程次数，那么怎么进行状态计算呢？我们可以枚举最后一次运送的状态，包括[1,2,3,…maxBoxeds]个箱子，那么枚举运送这些箱子能够产生的最小次数即可。

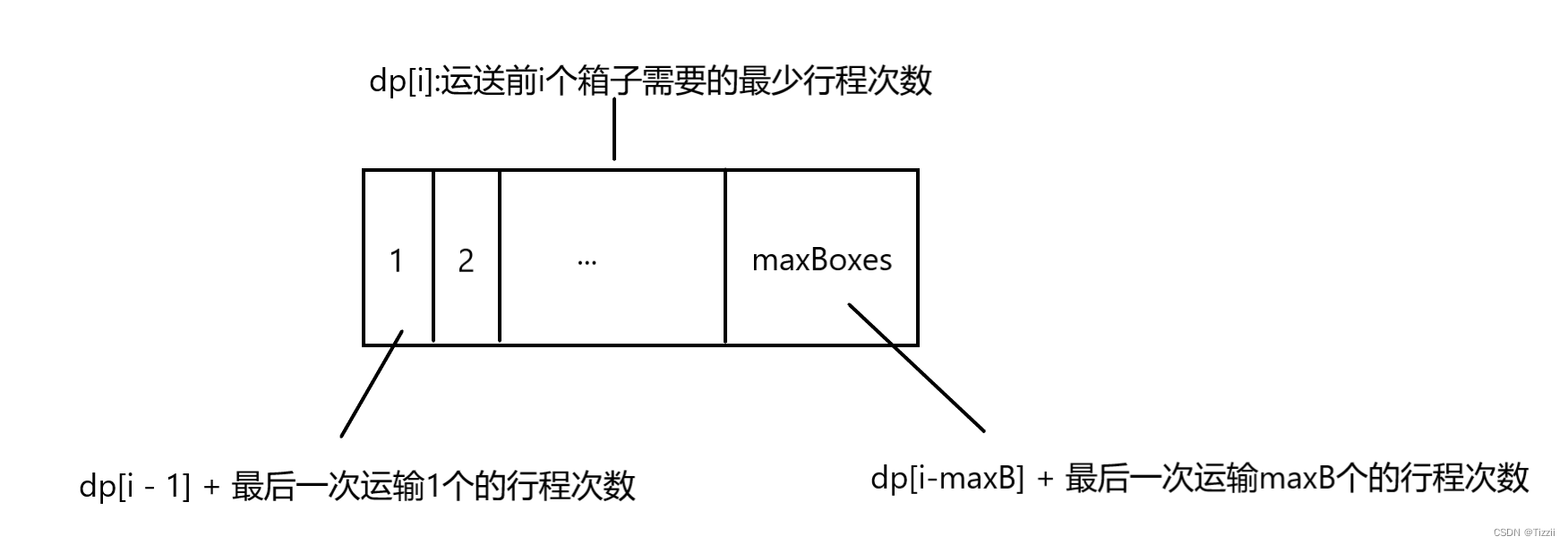
状态集合：
    dp[i]:运送前i个箱子需要的最少行程次数
状态计算：
    dp[i] = dp[j - 1] + cost[j, i],  (i - maxB + 1 <= j <= i)
    cost[j, i]代表第k~第i个箱子的行程次数

• 时间复杂度：$O(n^3)$
• 空间复杂度：$O(n)$

class Solution {
    public int boxDelivering(int[][] boxes, int portsCount, int maxBoxes, int maxWeight) {
        int n = boxes.length;
        int[] dp = new int[n + 5];
        Arrays.fill(dp, 0x3f3f3f3f);
        dp[0] = 0; //初始状态为0
        for (int i = 1; i <= n; i++) {
            int sum = 0;
            for (int j = i; j >= 1 && j >= i - maxBoxes + 1; j--) {
                sum += boxes[j - 1][1]; //累加箱子的种类之和
                if (sum > maxWeight) break; //超过了最大重量
                dp[i] = Math.min(dp[i], dp[j - 1] + cost(boxes, j, i));
            }
        }  
        return dp[n];
    } 
    int cost(int[][] boxes, int l, int r) {
        int ans = 2, port = boxes[l - 1][0]; //初始话为2,因为返回仓库算一次行程
        while (++l <= r) {
            if (boxes[l - 1][0] == port) continue; //只要相同，那么次数不会增加
            ans++;  //码头不相同运输次数增加1
            port = boxes[l - 1][0];
        }
        return ans;
    }
}

解法二：时间优化

我们首先从状态计算的角度去优化：

$dp[]$数组右边的所有式子可以看作在一个窗口内，窗口的大小为maxBoxes,而我们现在要求的是窗口中的最小值，并且随着$i$的增加窗口会向右移动。那么即转化为求滑动窗口的最小值，使用单调队列求解。


但是我们发现两段蓝色部分其实是有些地方不一样的，不一样的地方在于$cost$的右端点是不相同的。相比于前一层来说，当前层多了一个$i$端点。那么如何弥补这个差异呢，我们可以使用$dif$来表示$cost$的差异值,若前一个箱子$i-1$于当前箱子$i$的码头相同，那么并不会增加运输次数，那么这次的dif为0，否则就会增加1。由于我们无法直接在队列中进行修改，那么可以考虑增加一个累加值dif，具体看代码实现。


例如：若之前的窗口里面保存的次数为$[1,2,3]$，那么相对于当前进来值$dp[i-1]+cost[i,i]$来说要加上以前的差异dif进行比较后，继续构造一个单调递增的队列求解窗口的最小值。最后，将当前的次数$dp[i-1]+cost[i,i]-dif$放入队列中，减去一个dif是因为队列中保存的是一个相对的运输次数。


同理，我们还要判断重量是否超过了$maxWeight$, 一样的道理，我们创建一个变量$wei$来代表重量的偏差值，每次比较时，队列里面的重量要加上偏差值。


那么最后我们的队列里面就存放3个元素值，$a,b,c$, 其中$a$为该点的编号用来判断是否在窗口外，$b$为当前值的行程数，$c$为当前的重量之和。


$surprise$,至此可以发现我们不仅优化了第二个循环，顺带将cost函数也进行了优化。

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

class Solution {
    public int boxDelivering(int[][] boxes, int portsCount, int maxBoxes, int maxWeight) {
        int n = boxes.length;
        int[] dp = new int[n + 5];
        Arrays.fill(dp, 0x3f3f3f3f);
        dp[0] = 0;
        Deque<int[]> q = new ArrayDeque<int[]>(); //双端队列
        int dif = 0, wei = 0;
        for (int i = 1; i <= n; i++) {
            int cur = dp[i - 1] + 2;//cur为每次滑动窗口增加的值即dp[i-1]+cost[i,i]
            dif += i >= 2 && boxes[i - 1][0] != boxes[i - 2][0] ? 1 : 0;//dif为运输累加值，由于我们无法直接在队列中进行修改，那么可以考虑增加一个累加值
            wei += boxes[i - 1][1]; //重量要加上当前箱子的重量
            while (!q.isEmpty() && q.peekLast()[1] + dif >= cur) q.pollLast(); //构造一个单调递增的队列
            q.add(new int[]{i, cur - dif, boxes[i - 1][1] - wei}); 
            //判断左端队头是否在窗口外 并且重量不能超过最大重量
            while (q.peekFirst()[0] <= i - maxBoxes || q.peekFirst()[2] + wei > maxWeight) q.pollFirst(); 
            dp[i] = q.peekFirst()[1] + dif; 
        }  
        return dp[n];
    } 
}

解法三：空间优化

利用变量优化$dp$数组

• 时间复杂度：$O(n)$
• 空间复杂度：$O(k),k为滑动窗口大小$

class Solution {
    public int boxDelivering(int[][] boxes, int portsCount, int maxBoxes, int maxWeight) {
        int n = boxes.length, dp = 0;
        Deque<int[]> q = new ArrayDeque<int[]>();
        int dif = 0, wei = 0;
        for (int i = 1; i <= n; i++) {
            int cur = dp + 2;
            dif += i >= 2 && boxes[i - 1][0] != boxes[i - 2][0] ? 1 : 0;//cost[i, i] = 2
            wei += boxes[i - 1][1];
            while (!q.isEmpty() && q.peekLast()[1] + dif >= cur) q.pollLast();
            q.add(new int[]{i, cur - dif, boxes[i - 1][1] - wei}); 
            while (q.peekFirst()[0] <= i - maxBoxes || q.peekFirst()[2] + wei > maxWeight) q.pollFirst();
            dp = q.peekFirst()[1] + dif; 
        }  
        return dp;
    } 
}

解法四：优先队列

除了使用单调队列求解滑动窗口，那么还可以直接使用单调队列求解其中的最小值。

• 时间复杂度：$O(nlogn)$
• 空间复杂度：$O(n)$

class Solution {
    public int boxDelivering(int[][] boxes, int portsCount, int maxBoxes, int maxWeight) {
        int n = boxes.length, dp = 0;
        PriorityQueue<int[]> q = new PriorityQueue<int[]>((a, b)->a[1] - b[1]);
        int dif = 0, wei = 0;
        for (int i = 1; i <= n; i++) {
            int cur = dp + 2;
            dif += i >= 2 && boxes[i - 1][0] != boxes[i - 2][0] ? 1 : 0;//cost[i, i] = 2
            wei += boxes[i - 1][1]; 
            q.add(new int[]{i, cur - dif, boxes[i - 1][1] - wei}); 
            while (q.peek()[0] <= i - maxBoxes || q.peek()[2] + wei > maxWeight) q.poll();
            dp = q.peek()[1] + dif; 
        }  
        return dp;
    } 
}

Note: 另一种思路优化：

我们首先去观察如何优化cost数组，发现可以使用前缀和进行优化。

例如：$[1,2,2,3,4,3,3]$，这分别是不同码头的箱子，那么怎么快速计算$[l,r]$的运输次数。

那么我们可以首先初始化第一个箱子的运输次数$sum[1]=0$, 若当前箱子与前一个箱子相同，那么次数不会增加$sum[i]=sum[i-1]$，否则$sum[i]=sum[i-1]+1。$

最后，$sum=[0,1,1,2,3,4,4]$, 那么$cost[l,r]=sum[r]-sum[l]+2$。我们更新我们的状态计算如下：
那么利用前缀和数组计算的话，我们队列里面就只需要存储一下每个点的下标即可，例如$i-maxB+1,...，i-1$，每次通过下标来计算运输次数和重量即可。而解法二是直接优化前缀和数组，通过遍历答案时继续计算。

---

如果有问题,欢迎评论区交流, 如果有帮助到你，请给题解点个赞和收藏哈~~~