day16
- 104.二叉树的最大深度
- 559.n叉树的最大深度
- 111.二叉树的最小深度
- 222.完全二叉树的节点个数
104.二叉树的最大深度
题目链接
解题思路:本题中根节点的高度就是最大深度
二叉树节点的深度: 指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)
二叉树节点的高度: 指从该节点到叶子节点的最长简单路径边的条数或者节点数(取决于高度从0开始还是从1开始)
使用前序求的就是深度,使用后序求的是高度
- 确定递归函数的参数和返回值: 参数就是传入树的根节点,返回就返回这棵树的深度,所以返回值为int类型。
代码如下:
int getdepth(TreeNode* node)
- 确定终止条件: 如果为空节点的话,就返回0,表示高度为0。
代码如下:
if (node == NULL) return 0;
- 确定单层递归的逻辑: 先求它的左子树的深度,再求右子树的深度,最后取左右深度最大的数值 再+1(加1是因为算上当前中间节点)就是目前节点为根节点的树的深度。
代码如下:
int leftdepth = getdepth(node->left); // 左
int rightdepth = getdepth(node->right); // 右
int depth = 1 + max(leftdepth, rightdepth); // 中
return depth;
整体c++代码如下:
class solution {
public:
int getdepth(TreeNode* node) {
if (node == NULL) return 0;
int leftdepth = getdepth(node->left); // 左
int rightdepth = getdepth(node->right); // 右
int depth = 1 + max(leftdepth, rightdepth); // 中
return depth;
}
int maxDepth(TreeNode* root) {
return getdepth(root);
}
};
559.n叉树的最大深度
题目链接
解题思路:和上一题类似
class solution {
public:
int maxDepth(Node* root) {
if (root == 0) return 0;
int depth = 0;
for (int i = 0; i < root->children.size(); i++) {
depth = max (depth, maxDepth(root->children[i]));
}
return depth + 1;
}
};
111.二叉树的最小深度
题目链接
解题思路:
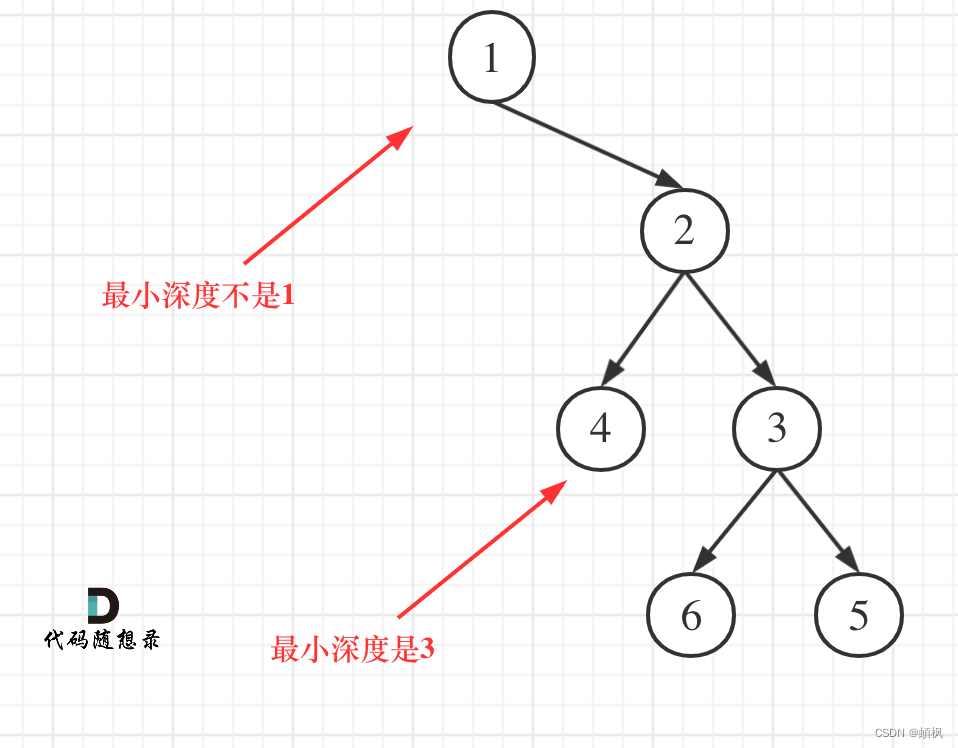
题目中说最小深度是从根节点到最近叶子节点的最短路径上的节点数量
叶子节点即左右孩子都为空的节点才是叶子节点
- 确定递归函数的参数和返回值
参数为要传入的二叉树根节点,返回的是int类型的深度。
代码如下:
int getDepth(TreeNode* node)
- 确定终止条件
终止条件也是遇到空节点返回0,表示当前节点的高度为0。
代码如下:
if (node == NULL) return 0;
- 确定单层递归的逻辑
如果左子树为空,右子树不为空,说明最小深度是 1 + 右子树的深度。
反之,右子树为空,左子树不为空,最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空,返回左右子树深度最小值 + 1 。
代码如下:
int leftDepth = getDepth(node->left); // 左
int rightDepth = getDepth(node->right); // 右
// 中
// 当一个左子树为空,右不为空,这时并不是最低点
if (node->left == NULL && node->right != NULL) {
return 1 + rightDepth;
}
// 当一个右子树为空,左不为空,这时并不是最低点
if (node->left != NULL && node->right == NULL) {
return 1 + leftDepth;
}
int result = 1 + min(leftDepth, rightDepth);
return result;
整体递归代码如下:
class Solution {
public:
int getDepth(TreeNode* node) {
if (node == NULL) return 0;
int leftDepth = getDepth(node->left); // 左
int rightDepth = getDepth(node->right); // 右
// 中
// 当一个左子树为空,右不为空,这时并不是最低点
if (node->left == NULL && node->right != NULL) {
return 1 + rightDepth;
}
// 当一个右子树为空,左不为空,这时并不是最低点
if (node->left != NULL && node->right == NULL) {
return 1 + leftDepth;
}
int result = 1 + min(leftDepth, rightDepth);
return result;
}
int minDepth(TreeNode* root) {
return getDepth(root);
}
};
222.完全二叉树的节点个数
题目链接
解题思路:
- 确定递归函数的参数和返回值:参数就是传入树的根节点,返回就返回以该节点为根节点二叉树的节点数量,所以返回值为int类型。
代码如下:
int getNodesNum(TreeNode* cur) {
- 确定终止条件:如果为空节点的话,就返回0,表示节点数为0。
代码如下:
if (cur == NULL) return 0;
- 确定单层递归的逻辑:先求它的左子树的节点数量,再求右子树的节点数量,最后取总和再加一
(加1是因为算上当前中间节点)就是目前节点为根节点的节点数量。
代码如下:
int leftNum = getNodesNum(cur->left); // 左
int rightNum = getNodesNum(cur->right); // 右
int treeNum = leftNum + rightNum + 1; // 中
return treeNum;
整体代码如下:
class Solution {
private:
int getNodesNum(TreeNode* cur) {
if (cur == NULL) return 0;
int leftNum = getNodesNum(cur->left); // 左
int rightNum = getNodesNum(cur->right); // 右
int treeNum = leftNum + rightNum + 1; // 中
return treeNum;
}
public:
int countNodes(TreeNode* root) {
return getNodesNum(root);
}
};