74. 搜索二维矩阵（中等）

在这里插入图片描述

方法一：二分查找

思路

总体思路

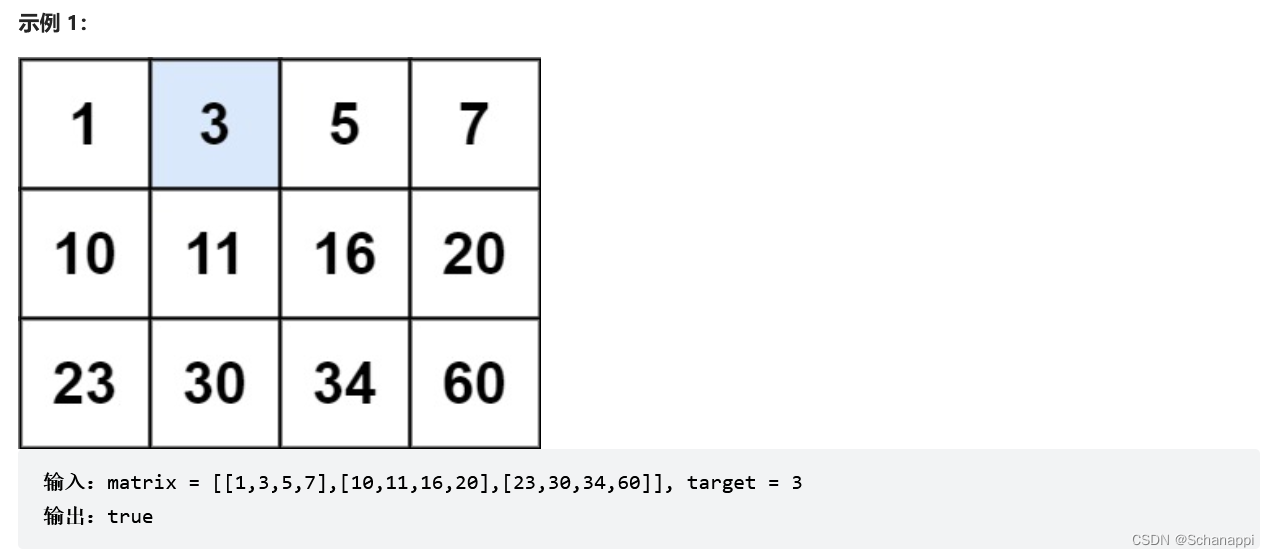
由于二维矩阵固定列的「从上到下」或者固定行的「从左到右」都是升序的
因此我们可以使用两次二分来定位到目标位置。
1. 第一次二分：从第 0 列中的「所有行」开始找，找到合适的行 row，即找到最后一个满足 matrix[x][0] <= target 的行号；
2. 第二次二分：从 row 中「所有列」开始找，找到合适的列 col ，即找到最后一个满足 matrix[row][y] <= target 的列号。

二分代码解释：

这里用到了二分查找的高级模板，left = mid，用于查找数组中当前索引及其直接左邻居索引的元素或条件。

注意，while 语句的条件是 left < right 。

此外，mid 值计算需要 +1 ，如果不加 1 会出现死循环（比如l = 2, r = 3 的时候，如果不加 1，在满足 l = mid 的情况下，会一直死循环）。

int binarySearch(vector<int>& nums, int target){
	  if(nums.size() == 0)
	  	return -1;

 	 int left = 0, right = nums.size();
  		while(left < right){
	    // Prevent (left + right) overflow
	    int mid = left + (right - left) / 2;
	    if(nums[mid] == target){ return mid; }
	    else if(nums[mid] <= target) { left = mid; }
	    else { right = mid + 1; }
	  }

	  // Post-processing:
	  // End Condition: left == right
	  if(left != nums.size() && nums[right] == target) return right;
	  return -1;
	}

代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int row, col;
        int left = 0, right = m-1;
        // 第一次二分找到最后一个不大于目标值的元素的所在行
        while(left < right){
            int mid = left + (right - left + 1) / 2;
            if(matrix[mid][0] <= target)  left = mid;
            else right = mid - 1;
        }
        row = right;

        // 可以先判断，减少时间复杂度
        if(matrix[row][0] == target) return true;
        if(matrix[row][0] > target) return false;

        // 第二次二分找到所在列
        left = 0, right = n-1;
        while(left<right){
            int mid = left + (right - left + 1) / 2;
            if(matrix[row][mid] <= target)   left = mid;
            else right = mid - 1;
        }
        col = right;
        return matrix[row][col] == target;
    }
};

方法二：一次二分

思路

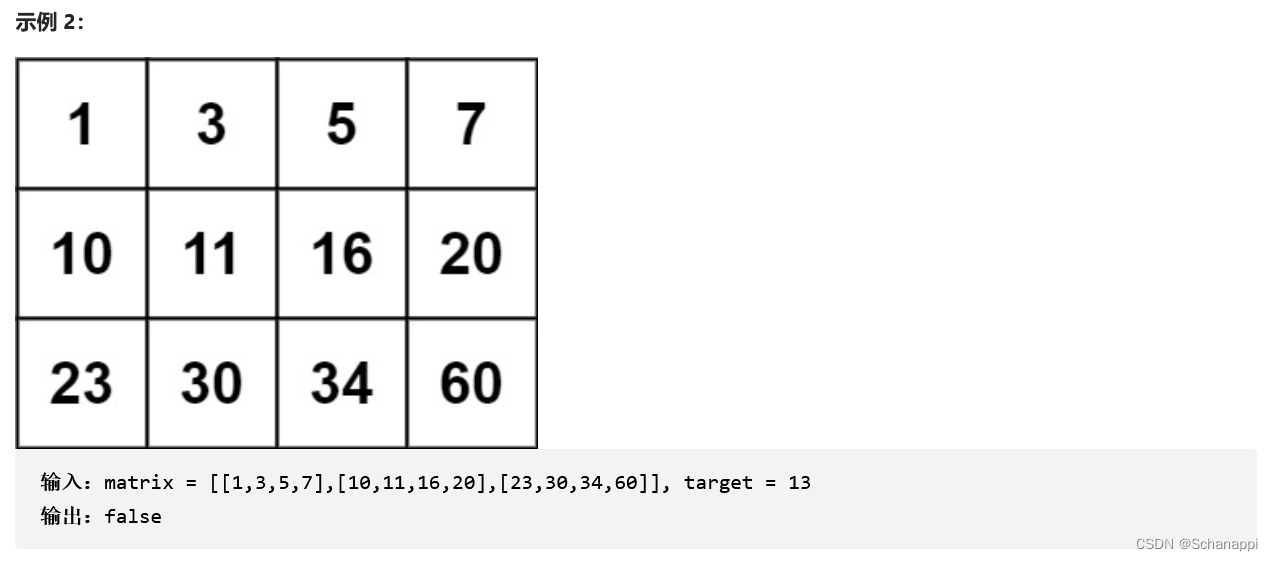
如果将数组按行逐元素连接起来，那么数组将形成一个单调递增序列，我们可以使用一次二分在该 “一维数组” 中查找，如果找到target ，返回 true；否则返回false。
对于一次二分，因为只有找到 target 和没找到 target 两种情况，所以只需要普通的模板。

代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int left = 0, right = m * n - 1;
        // 一次二分
        while(left <= right){
            int mid = left + (right - left) / 2;
            if(matrix[mid/n][mid%n] == target) return true;
            else if(matrix[mid/n][mid%n] < target) left = mid + 1;
            else right = mid - 1;             
        }
        return false;
    }
};

方法三：抽象二叉搜索树

思路

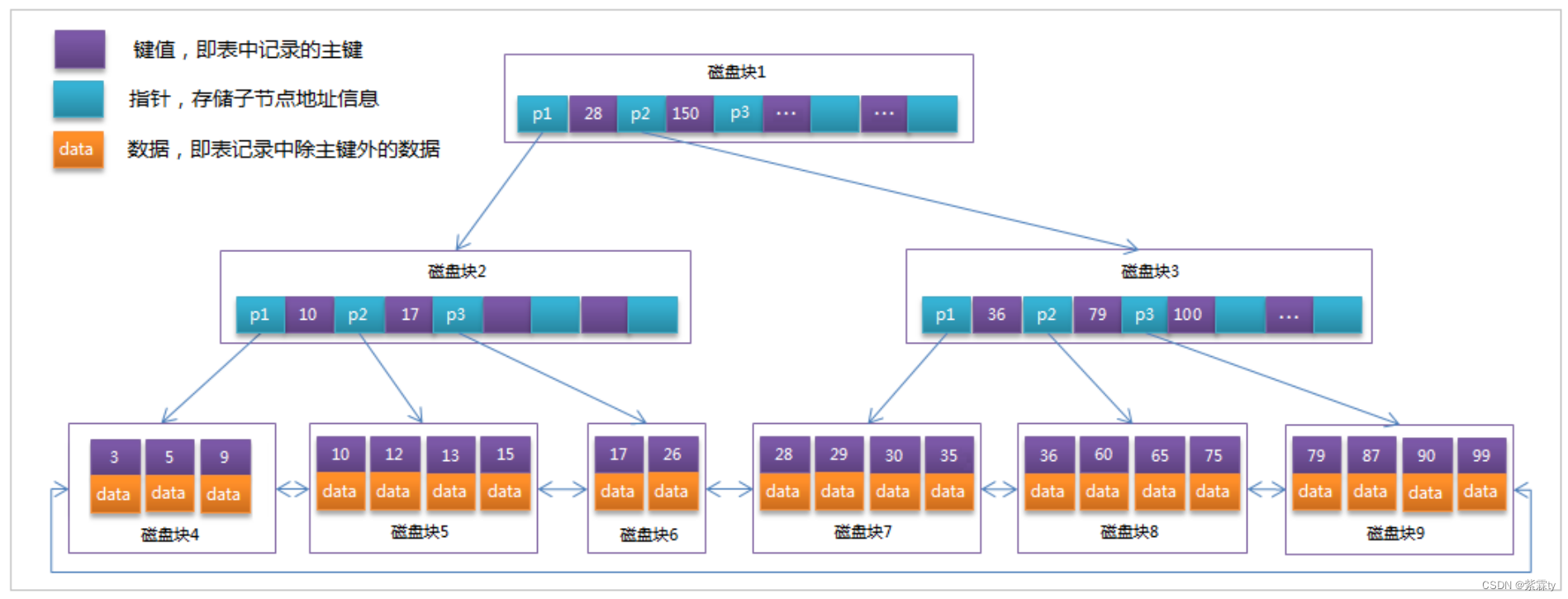
我们可以将二维矩阵抽象成「以右上角为根的 BST」：
那么我们可以从根（右上角）开始搜索，如果当前的节点不等于目标值，可以按照树的搜索顺序进行：
- 当前节点「大于」目标值，搜索当前节点的「左子树」，也就是当前矩阵位置的「左方格子」，即 y–；
- 当前节点「小于」目标值，搜索当前节点的「右子树」，也就是当前矩阵位置的「下方格子」，即 x++。

代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        // 当前的坐标值，从右上角开始查找
        int x = 0, y = n-1;

        while(check(x, y, m, n) && matrix[x][y] != target){
            // 如果matrix[x][y] > target 说明需要向左查找
            if(matrix[x][y] > target)   y--;
            // 如果matrix[x][y] > target 说明需要向下查找
            else if(matrix[x][y] < target)  x++;
        }
        
        return check(x, y, m, n) && matrix[x][y] == target;
    }
    // 边界情况判断
    bool check(int x, int y, int m, int n){
        return x>=0 && x<m && y>=0 && y<n;
    }
};