往期回顾

WPF 学习：如何使用实时可视化树，照着MaterialDesign的Demo学习

可视化页面元素

我们知道，网页的页面元素是可以通过按F12查看代码。查看到页面元素的。

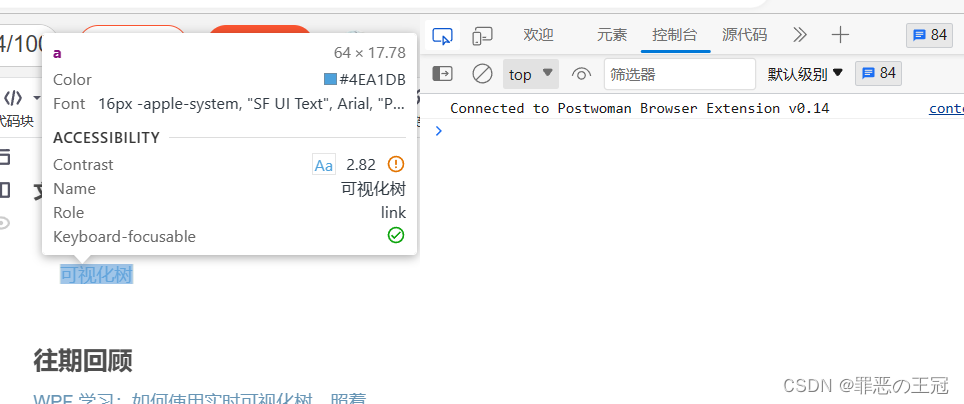
WPF也有类似的工具，在我们debug运行的时候，就会有对应的调试工具

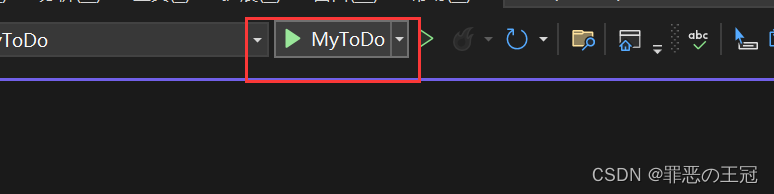
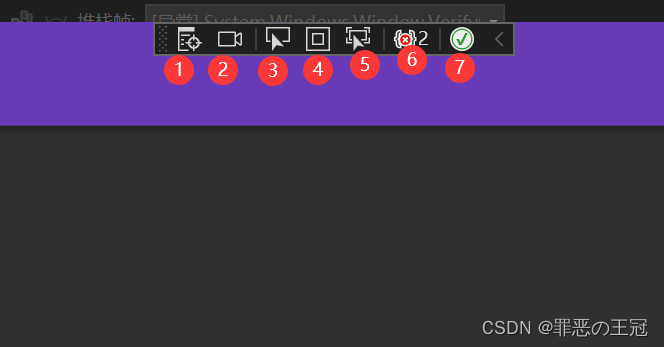
序号	作用
1	转到选择元素的实时可视化树
2	编译器预览运行界面
3	选择页面元素，所以一般是先3后1
4	边框显示
5	跟踪具有焦点的元素，不知道有啥用
6	页面元素运行报错，这个是页面元素的资源是否正确引入。
7	是否开启xmal热重载，√为已开启

如何使用调试工具

实时可视化树平常藏在左上角

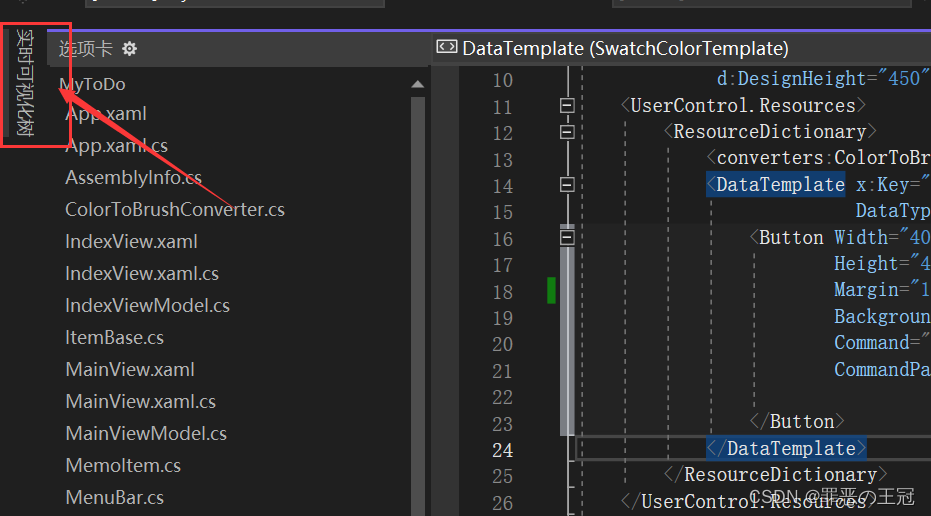
运行的时候点开

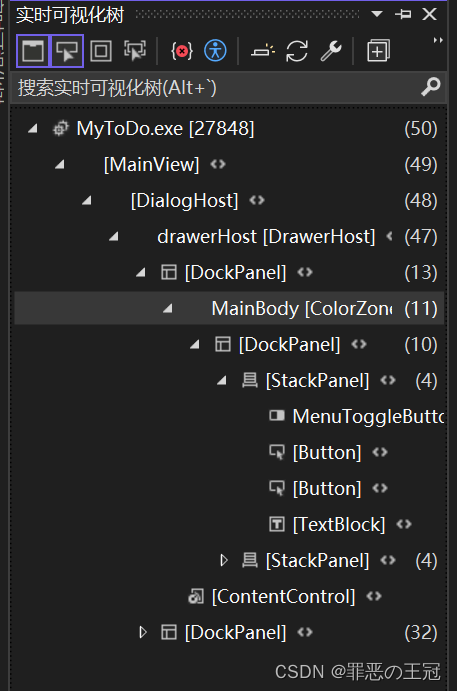
右边的<>是查看源码

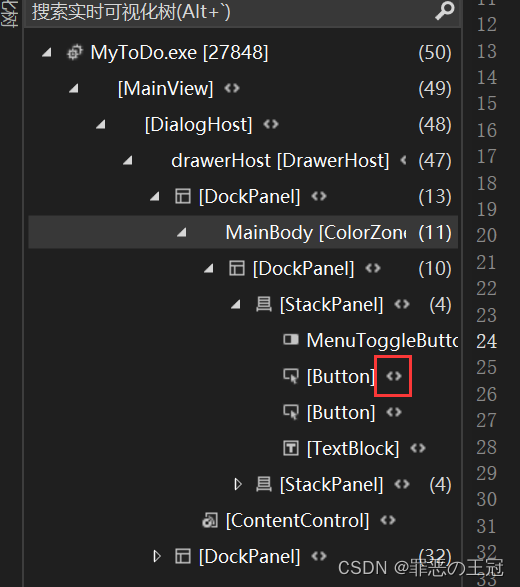
使用示例

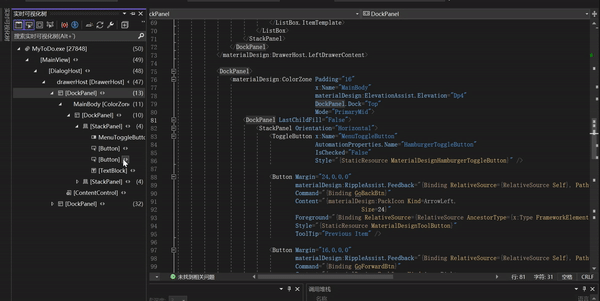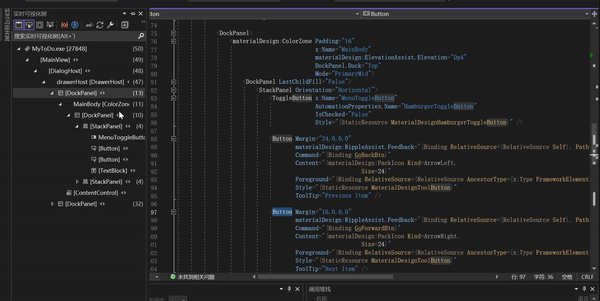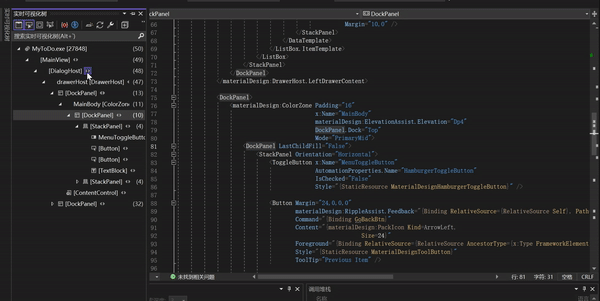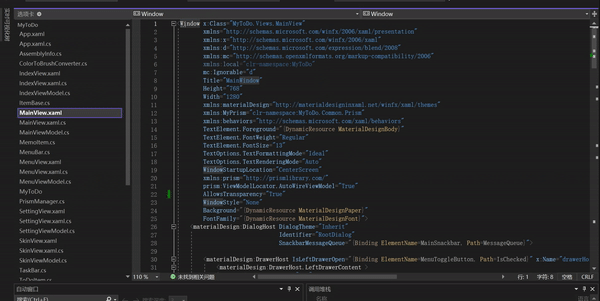
点击2会有个实时预览缩略图，但是会比较小

我将其放大，你选择实时可视化树的左侧，右侧对应的页面元素就会发亮。如果你点击右侧的页面元素，左侧的实例化树也会跳转到对应的位置

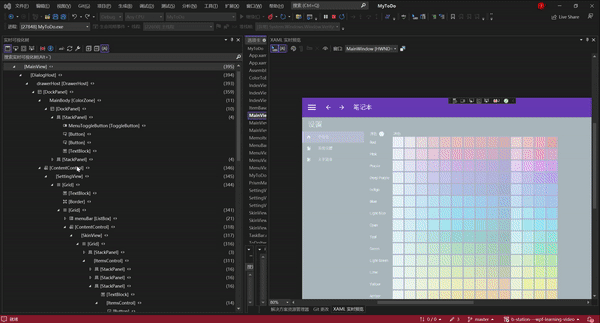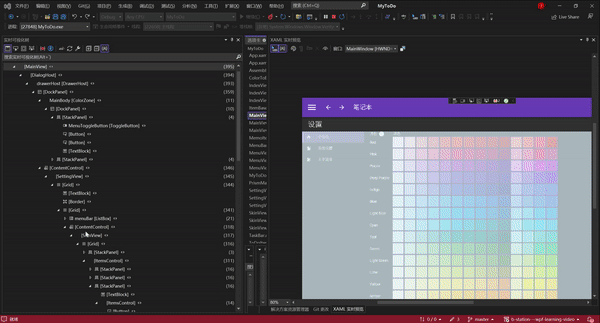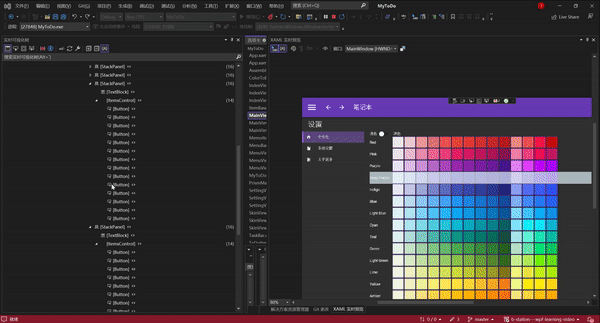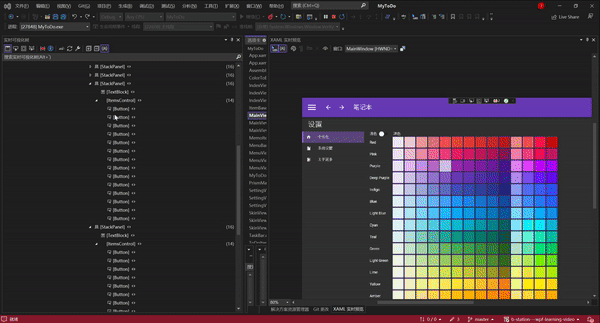
如果你有两个屏幕，看的就会更加清楚。
一边是页面，一边是代码

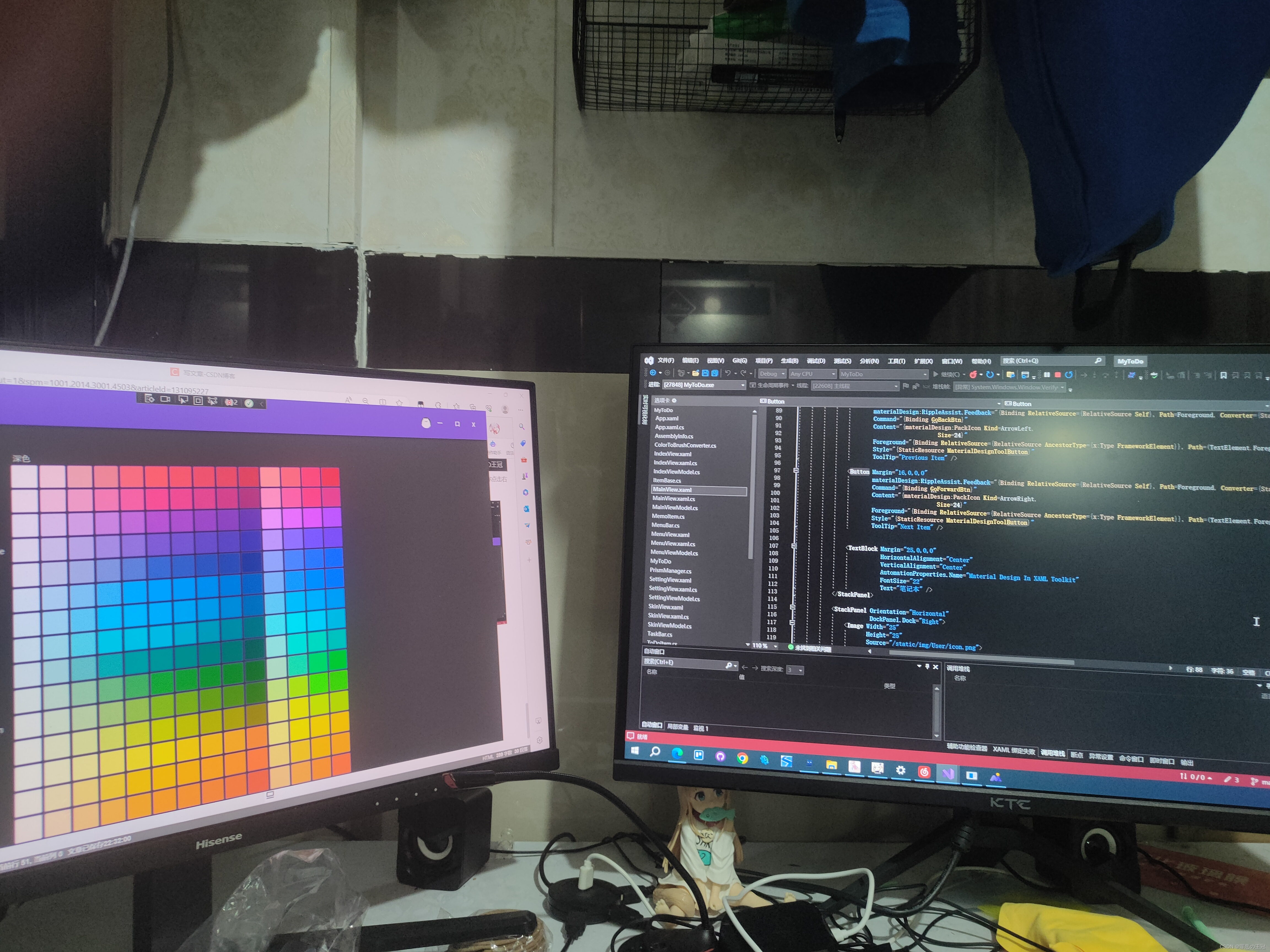
总结

如何使用调试工具介绍完毕。