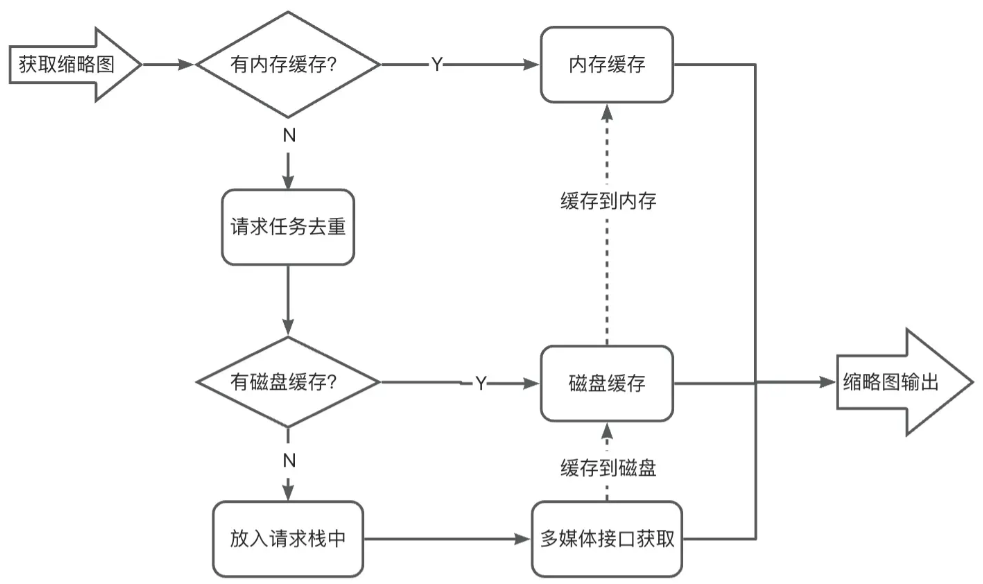
线性回归

最小二乘法

对于某数据量 $x$ 有呈线性关系的输出量 $y$ ，且 $y=a_{1}x+a_{2}$ ，现有对这些数据量的采集序列 $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})...$ ，这些采集量会存在随机误差 $v_{1},v_{2},v_{3}...$ ，线性回归的目的便是找到保证使误差最小的情况下的回归系数 $a_{1},a_{2 }$ 。

即通过下列方程组求 $min(v_1^2+v_2^2+v_3^2+...)$

$v_{1}=y_{1}-(a_{1}x_{1}+a_{2})\\ v_{2}=y_{2}-(a_{1}x_{2}+a_{2})\\ v_{3}=y_{3}-(a_{1}x_{3}+a_{2})...$

可利用最小二乘法，先获取正规方程：
系数矩阵 $A$ 为

$\begin{bmatrix} x_1&1 \\ x_2 & 1 \\ x_3& 1\\ ... \end{bmatrix}$

误差向量 $V$ 为
$\begin{bmatrix} v_1\\ v_2\\ v_3\\ ... \end{bmatrix}$
回归系数向量 $X$ 为
$\begin{bmatrix} a_1\\ a_2\\ \end{bmatrix}$

输出向量 $Y$ 为
$\begin{bmatrix} y_1\\ y_2\\ y_3\\ ... \end{bmatrix}$

正规方程为 $A^{T}V=0$ ，由于 $V=Y-AX$ ，故 $X=(A^TA)^{-1}A^TY$ 。

由此得到回归系数 $X$ 。对于不等精度测量，只需在误差向量前乘上权值向量 $P$ 即可。

最小二乘法精度估计

最小二乘法所得到的回归系数 $X$ 的精度取决于测量数据集的精度，有不定乘数矩阵

$D=(A^TA)^{-1 }$ ，对于等精度测量所得 $Y$ ，其标准差为 $\sigma$ ，则估计量 $X$ 的协方差为

$D(X)=D\sigma ^2$ ，若为不等精度测量，则 $D=(A^TPA)^{-1}$ 。

对于多元线性回归，仍采用最小二乘法求解。

线性递推回归

上述回归，是基于一次性得到全部测量结果计算的，而在动态测量中，数据数量是逐渐增加的，若需实时进行回归处理，那么每当获得一个新数据便需要及时解出回归方程的新系数，解法如下。

假如已经采集了 $N$ 组数据，那么根据上述正规方程的解法有 $X_N=(A_N^TA_N)^{-1}A_N^TY$ ，此时新加入测量量 $x_{1_{N+1}},x_{2_{N+1}},x_{3_{N+1}}...y_{N+1}$ ，令 $x_{N+1}=(x_{1_{N+1}},x_{2_{N+1}},x_{3_{N+1}}...)$ 则