1.分类变量

分类变量是用来表示类别或标记的。在实际的数据集中，类别的数量总是有限的。类别可以用数字表示，但与数值型变量不同，分类变量的值是不能被排序的。（作为行业类型，石油和旅游之间是分不出大小的。）它们又称为无序变量。

2.分类变量的编码

分类变量中的类别通常不是数值型的。 1 例如，眼睛的颜色可以是“黑色”“蓝色”和“褐色”，等等。因此，需要一种编码方法来将非数值型的类别转换为数值。我们很容易想到，可以简单地为 k 个可能类别中的每个类别分配一个整数，如从 1 到 k，但这样做的结果是使类别彼此之间有了顺序，这在分类变量中是不允许的。

2.1one-hot编码

使用一组比特位，每个比特位表示一种可能的类别。如果变量不能同时属于多个类别，那么这组值中就只有一个比特位是“开”的。这就是 one-hot 编码，它可以通过 scikit-learn 中的 sklearn.preprocessing.OneHotEncoder 实现。每个比特位表示一个特征，因此，一个可能有 k 个类别的分类变量就可以编码为一个长度为 k 的特征向量。

one-hot 编码很容易理解，但它使用的比特位要比实际需要的多一位。如果 k-1 位都是 0，那么最后一位肯定是 1，因为变量必须取 k 个值中的一个。

e 1 + e 2 + … + e k = 1

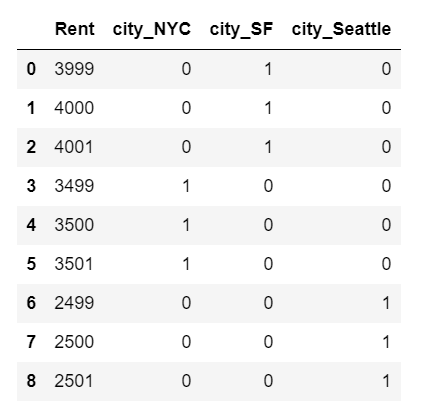
例如：三个类别分别是：[0,0,1],[0,1,0],[1,0,0]

使用 one-hot 编码时，截距项表示目标变量 Rent 的整体均值，每个线性系数表示相应城市
的租金均值与整体均值有多大差别。

import pandas as pd
from sklearn import linear_model
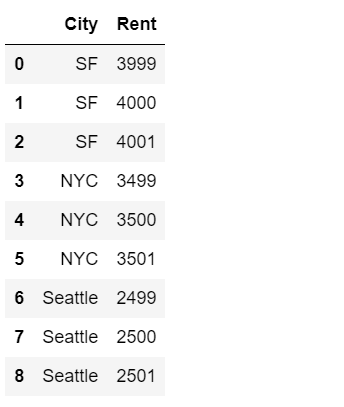
df = pd.DataFrame({'City': ['SF', 'SF', 'SF', 'NYC', 'NYC', 'NYC', 'Seattle', 'Seattle', 'Seattle'],
                   'Rent': [3999, 4000, 4001, 3499, 3500, 3501, 2499, 2500, 2501]})
df

在这里插入图片描述

one_hot_df = pd.get_dummies(df, prefix=['city'])

one_hot_df

在这里插入图片描述

lin_reg = linear_model.LinearRegression()
x = one_hot_df[['city_NYC', 'city_SF', 'city_Seattle']]
y = one_hot_df['Rent']
lin_reg.fit(x, y)
# 模型参数
print(lin_reg.coef_)

# 截距项
lin_reg.intercept_

2.2虚拟编码

one-hot 编码的问题是它允许有 k 个自由度，而变量本身只需要 k-1 个自由度。虚拟编码在进行表示时只使用 k-1 个特征，除去了额外的自由度。没有被使用的那个特征通过一个全零向量来表示，它称为参照类。虚拟编码和 one-hot 编码都可以通过 Pandas包中的 pandas.get_dummies 来实现。
即三个类分别是：[0,0],[0,1],[1,0]

使用虚拟编码时，偏差系数表示响应变量 y 对于参照类的均值，本例中参照类是纽约。第 i个特征的系数等于第 i 个类别的均值与参照类均值的差。

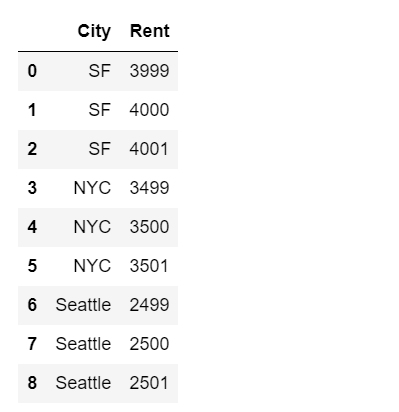
df = pd.DataFrame({'City': ['SF', 'SF', 'SF', 'NYC', 'NYC', 'NYC', 'Seattle', 'Seattle', 'Seattle'],
                   'Rent': [3999, 4000, 4001, 3499, 3500, 3501, 2499, 2500, 2501]})
df

在这里插入图片描述

dummy_df = pd.get_dummies(df, prefix=['city'], drop_first=True)
dummy_df

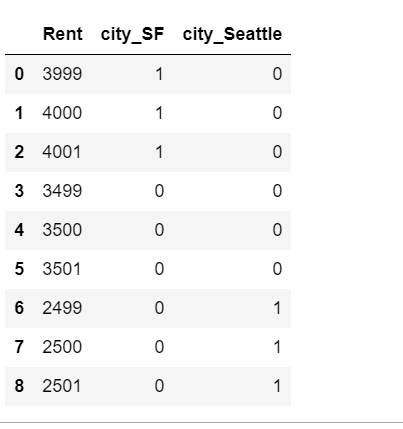
在这里插入图片描述
用虚拟编码构成的特征训练模型

lin_reg2 = linear_model.LinearRegression()
lin_reg2.fit(dummy_df[['city_SF', 'city_Seattle']], dummy_df['Rent'])
print(lin_reg2.coef_)
lin_reg2.intercept_

2.3效果编码

另一种分类变量编码是效果编码。效果编码与虚拟编码非常相似，区别在于参照类是用全部由 -1 组成的向量表示的。效果编码与虚拟编码非常相似，但它的线性回归模型更容易解释。截距项表示目标变量的整体均值，各个系数表示了各个类别的均值与整体均值之间的差。（这称为类别或水平的主效果，效果编码的名称就是由此而来。）one-hot 编码实际上也可以得到同样的截距和系数，但它的每个城市都有一个线性系数。在效果编码中，没有单独的特征来表示参照类，所以参照类的效果需要单独计算，它是所有其他类别的系数的相反数之和。

df = pd.DataFrame({'City': ['SF', 'SF', 'SF', 'NYC', 'NYC', 'NYC', 'Seattle', 'Seattle', 'Seattle'],
                   'Rent': [3999, 4000, 4001, 3499, 3500, 3501, 2499, 2500, 2501]})
dummy_df = pd.get_dummies(df, prefix=['city'], drop_first=True)

effect_df = dummy_df.copy()
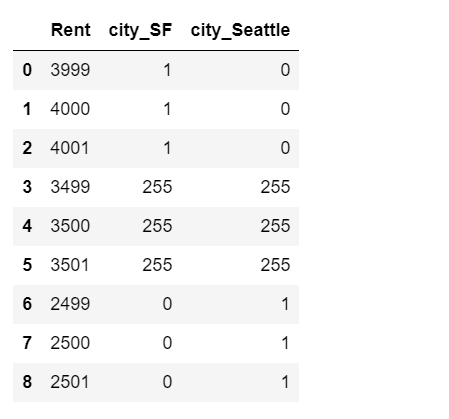
effect_df.loc[3:5, ['city_SF', 'city_Seattle']] = -1.0
effect_df

在这里插入图片描述

2.4各种分类变量编码的优缺点

one-hot编码有冗余，这会使得同一个问题有多个有效模型，这种非唯一性有时候比较难以解释。它的优点是每个特征都明确对应一个类别，而且可以把缺失数据编码为全零向量，模型输出也是目标变量的总体均值。

虚拟编码和效果编码没有冗余，它们可以生成唯一的可解释的模型。虚拟编码的缺点是不太容易处理缺失数据，因为全零向量已经映射为参照类了。它还会将每个类别的效果表示为与参照类的相对值，这看上去有点不直观。

效果编码使用另外一种编码表示参照类，从而避免了这个问题，但是全由 -1 组成的向量是个密集向量，计算和存储的成本都比较高。

当类别的数量变得非常大时，这 3 种编码方式都会出现问题，所以需要另外的策略来处理超大型分类变量。

3.处理大型分类变量

互联网上的自动数据采集可以生成大型分类变量，在定向广告和欺诈检测这样的应用中，这种情况非常常见。

在定向广告应用中，我们的任务是为一个用户匹配一组广告。这时的特征包括用户 ID、广告的站点域名、查询语句、当前页以及这些特征的所有成对组合。（查询语句是一个文本字符串，可以被分解转换成一般的文本特征。但是，查询语句一般很短，而且通常由短语组成，所以这时最好的做法是保持它们原封不动或者通过一个散列函数来传递，以使得存储和比较更加容易。这些特征中的每一个都是非常巨大的分类变量，面临的挑战就是找到一种合适的特征表示方法，既要内存高效，又能生成精确的、训练速度很快的模型。解决方案如下：

(1) 不在编码问题上搞什么花样，使用一个简单、容易训练的模型，在很多机器上使用one-hot 编码训练线性模型（逻辑回归或线性支持向量机）。

(2) 压缩特征，有两种方式。

a) 特征散列化，通常用于线性模型。
b) 分箱计数，常用于线性模型和树模型。

3.1压缩特征-特征散列化

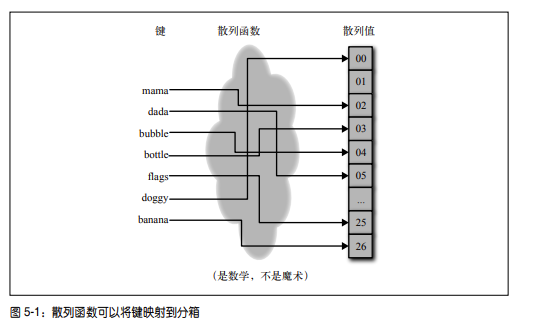
散列函数是一种确定性函数，它可以将一个可能无界的整数映射到一个有限的整数范围[1, m] 中。因为输入域可能大于输出范围，所以可能有多个值被映射为同样的输出，这称为碰撞。均匀散列函数可以确保将大致相同数量的数值映射到 m 个分箱中。以形象地将散列函数想象为一台机器，它吸入一些带数字标号的圆球（键），再把它们分发到 m 个分箱中。标有同样数字的球总是被分发到同一个分箱中。散列函数在保持特征空间的同时，又可以在机器学习的训练和评价周期中减少存储空间和处理时间。

当特征很多时，保存特征向量需要大量空间。通过对特征 ID 应用散列函数，特征散列化可以将初始特征向量压缩为 m 维向量;

如果模型中涉及特征向量和系数的内积运算，那么就可以使用特征散列化，比如线性模型和核方法。

特征散列化的一个缺点是散列后的特征失去了可解释性，只是初始特征的某种聚合。特征离散化减少了存储空间占用。

可以形象地将散列函数想象为一台机器，它吸入一些带数字标号的圆球（键），再把
它们分发到 m 个分箱中。标有同样数字的球总是被分发到同一个分箱中（见图 5-1）。散列
函数在保持特征空间的同时，又可以在机器学习的训练和评价周期中减少存储空间和处理
时间。
在这里插入图片描述
散列化算法原理实现：

# 单词特征的特征散列化
def hash_features(word_list, m):
    output = [0] * m
    for word in word_list:
        index = hash_fcn(word) % m
        output[index] += 1
    return output

# 带符号的特征散列化  : 确保散列后特征之间的内积等于初始特征内积的期望。
def hash_features(word_list, m):
    output = [0] * m
    for word in word_list:
        index = hash_fcn(word) % m
        sign_bit = sign_hash(word) % 2
        if (sign_bit == 0):
            output[index] -= 1
        else:
            output[index] += 1
    return output

实际案例
使用 scikit-learn 的 FeatureHasher 函数，在 Yelp 点评数据集上演示存储空间和解释性的这种取舍。

# 加载数据
# 存储空间与解释性的取舍
import pandas as pd
import json

f = open(r'..\data\yelp_academic_dataset_review.json')
js = []
for i in range(10000):
    js.append(json.loads(f.readline()))
f.close()
review_df = pd.DataFrame(js)
# 定义m为唯一的business_id的数量
m = len(review_df.business_id.unique())
review_df.shape

from sklearn.feature_extraction import FeatureHasher

h = FeatureHasher(n_features=m, input_type='string')
business_id_data = [ [r] for r in review_df['business_id'].tolist()]
f = h.transform(business_id_data)
# 散列化对特征可解释性的影响
business_id_data[0:5],f.toarray()

# 占用空间对比
from sys import getsizeof

print('Our pandas Series, in bytes: ', getsizeof(review_df['business_id']))
print('Our hashed numpy array, in bytes: ', getsizeof(f))

Our pandas Series, in bytes:  790144
Our hashed numpy array, in bytes:  48

3.2压缩特征-分箱计数

箱计数是机器学习中的重新发现之一，从广告点击率预测到硬件分支预测，很多应用都对它进行了改造并使用。分箱计数的思想稍有一点复杂：它不使用分类变量的值作为特征，而是使用目标变量取这个值的条件概率。换句话说，不对分类变量的值进行编码，而是要计算分类变量值与要预测的目标变量之间的相关统计量。对于那些熟悉朴素贝叶斯分类器的人来说，这个统计量肯定耳熟能详，因为它就是在所有特征都是独立的这个假设之下的各个类别的条件概率。

分箱计数将一个分类变量转换为与其值相关的统计量，它可以将一个大型的、稀疏的、二值的分类变量表示（如 one-hot 编码生成的结果）转换为一个小巧的、密集的、实数型的数值表示。

用于分箱计数的优势比和对数优势比：

优势比是指某种推测为真的概率与某种推测为假的概率的比值。比如下雨的概率为0.25，不下雨的概率为0.75。0.25与0.75的比值可以约分为1比3。因此，我们可以说今天将会下雨的优势比为1:3(或者今天不会下雨的概率比为3:1)。
对数优势比: 主要用于检验两个基因座间是否彼此连锁的可能性。对数优势比为正值，有利于连锁；对数优势比为零，意味连锁与不连锁的可能性各为50%；对数优势比为负值，表示有一定重组值的连锁。对数优势比为+3时，连锁概率为0.95；对数优势比为-2时，不连锁的概率为0.95。

为了实际演示一下分箱计数，我们要使用一下由 Avazu 主办的 Kaggle 竞赛中的数据。下
面是这个数据集的几个相关统计量。
• 共有 24 个变量，其中 click 是个二值计数器，值为 click 和 no click，device_id 用来跟踪广告显示在哪个设备上。
• 整个数据集包括 40 428 967 条观测，使用了 2 686 408 台独立的设备

Avazu 竞赛的目标是使用广告数据预测点击率，但我们要使用这个数据集做一个演示，说
明对于大量的流式数据，分箱计数是如何显著缩减特征空间的。

df = pd.read_csv(r'..\data\train_subset.csv')
len(df['device_id'].unique())#查看数据集中有多少个唯一的特征

# 对每个类别，要计算：
# Theta = [counts, p(click), p(no click), p(click)/p(no click)]
def click_counting(x, bin_column):
    clicks = pd.Series(x[x['click'] > 0][bin_column].value_counts(), name='clicks')
    no_clicks = pd.Series(x[x['click'] < 1][bin_column].value_counts(), name='no_clicks')
    
    counts = pd.DataFrame([clicks,no_clicks]).T.fillna('0')
    counts['total'] = counts['clicks'].astype('int64') + counts['no_clicks'].astype('int64')
    
    return counts

def bin_counting(counts):
    # divide：除法
    counts['N+'] = counts['clicks'].astype('int64').divide(counts['total'].astype('int64'))
    counts['N-'] = counts['no_clicks'].astype('int64').divide(counts['total'].astype('int64'))
    counts['log_N+'] = counts['N+'].divide(counts['N-'])
    #如果只想返回分箱属性就进行过滤
    bin_counts = counts.filter(items= ['N+', 'N-', 'log_N+'])
    return counts, bin_counts

# 对device_id进行分箱计数:
bin_column = 'device_id'
device_clicks = click_counting(df.filter(items= [bin_column, 'click']), bin_column)
device_all, device_bin_counts = bin_counting(device_clicks)

len(device_bin_counts)

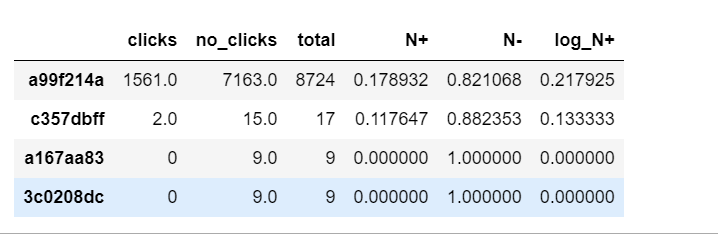
device_all.sort_values(by = 'total', ascending=False).head(4)

在这里插入图片描述

3.3如何处理稀有类

和罕见词一样，稀有类也需要特殊处理。设想一个一年只登录一次的用户：只有极少的数据能用来可靠地估计这个用户的广告点击率。而且，稀有类还会浪费计数表中的空间。

解决这个问题的一种方法称为 back-off，这是一种将所有稀有类的计数累加到一个特殊分箱中的简单技术;如果类别的计数大于一个确定的阈值，那么就使用它自己的计数统计量；否则，就使用 back-off 分箱的统计量。这种方法本质上就是把单个稀有类的统计量转换为使用所有稀有类计算的统计量。当使用 back-off 方法时，可以添加一个表示统计量是否来自于 back-off 分箱的二值指示器。
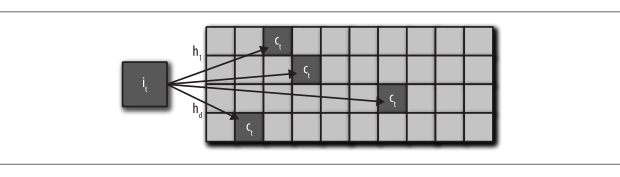
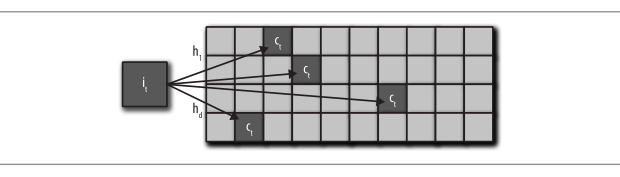
在这里插入图片描述

解决这个问题的另外一种方法称为最小计数图（Cormode and Muthukrishnan, 2005）。在这种方法中，不管是稀有类还是频繁类，所有类别都通过多个散列函数进行映射，每个散列函数的输出范围 m 都远远小于类别数量 k。在计算统计量时，需要使用所有散列函数进行计算，并返回结果中最小的那个统计量。与使用单散列函数相比，使用多个散列函数可以降低碰撞概率。这种方法的有效之处在于，散列函数的数量乘以散列表大小 m 之后，不但可以小于类别数量 k，而且能保持非常低的碰撞概率。
在这里插入图片描述

3.4防止数据泄露

因为分箱计数要依赖历史数据生成必需的统计量，所以它需要等待一段时间以完成数据收集，这就会在学习流程中导致一点轻微的延迟。还有，当数据分布改变时，需要更新计数。数据变化得越快，计数重新计算的频率就越高。在像定向广告这样的应用中，用户偏好和常用查询变化得非常快，所以这个问题变得特别重要，不能适应当前数据分布的变化意味着广告平台的巨大损失。数据泄露。

简单地说，数据泄露会使模型中包含一些不应该有的信息，这些信息可以使模型获得某种不现实的优势，从而做出更加精确的预测。出现数据泄露有多种原因，比如测试数据泄露到训练数据中，或者未来数据泄露到过去数据中。 只要模型获得了在生产环境中实时预测时不应该接触到的信息，就会发生数据泄露。

解决方法:

使用过去的数据点进行计数，使用当前的数据点进行训练（将分类变量映射到我们前面收集到的历史统计量上），再使用未来的数据点进行测试。这可以解决数据泄露问题，但会引发前面提过的流程延迟问题。
对于一个统计量，如果不管有没有任何一个数据点，它的分布都保持基本不变，那么它就是近似防漏的。实际上，使用 Laplace(0,1) 分布添加一个小的随机噪声，就足以弥补任何来自单数据点的潜在泄露。

3.5无界计数

当输入计数增加时，模型需要维持原来的规模。如果计数累积得比较慢，有效范围不会变得太快，模型就不需要维护得特别频繁。但当计数增加得非常快时，过于频繁的维护就会造成很多问题。由于这个原因，通常更好的做法是使用归一化后的计数，这样就可以保证把计数值限制在一个可知的区间中。例如，点击率的估计值被限制在 [0, 1] 这一范围。另一种方法是进行对数变换，这样可以强加一个严格的边界，但当计数值非常大时，变换结果的增加速度是非常慢的。