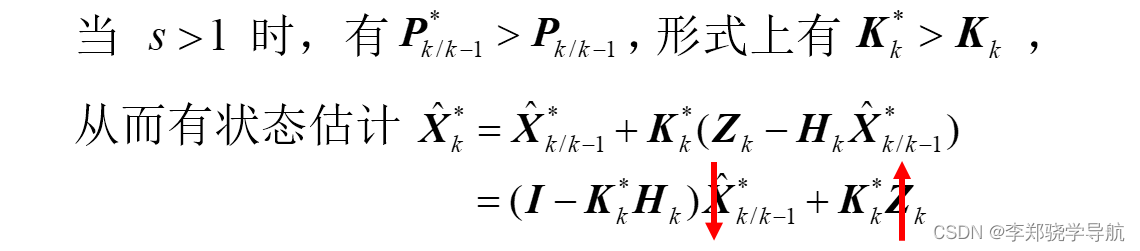函数模型
{
X
k
=
Φ
k
l
k
−
1
X
k
−
1
+
Γ
k
−
1
W
k
−
1
Z
k
=
H
k
X
k
+
V
k
\left\{\begin{array}{l} \boldsymbol{X}_{k}=\boldsymbol{\Phi}_{k l k-1} \boldsymbol{X}_{k-1}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1} \\ \boldsymbol{Z}_{k}=\boldsymbol{H}_{k} \boldsymbol{X}_{k}+\boldsymbol{V}_{k} \end{array}\right.
{Xk=Φklk−1Xk−1+Γk−1Wk−1Zk=HkXk+Vk
随机模型
{
E
[
W
k
]
=
0
,
E
[
W
k
W
j
T
]
=
s
N
−
k
+
1
Q
k
δ
k
j
j
,
k
≤
N
E
[
V
k
]
=
0
,
E
[
V
k
V
j
T
]
=
s
N
−
k
R
k
δ
k
j
E
[
W
k
V
j
T
]
=
0
\left\{\begin{array}{ll}\mathrm{E}\left[\boldsymbol{W}_{k}\right]=\mathbf{0}, & \mathrm{E}\left[\boldsymbol{W}_{k} \boldsymbol{W}_{j}^{\mathrm{T}}\right]={\color{green}s^{N-k+1}}\boldsymbol{Q}_{k} \delta_{k j}\quad j,k \le N\\ \mathrm{E}\left[\boldsymbol{V}_{k}\right]=\mathbf{0}, & \mathrm{E}\left[\boldsymbol{V}_{k} \boldsymbol{V}_{j}^{\mathrm{T}}\right]={\color{green}s^{N-k}} \boldsymbol{R}_{k} \delta_{k j} \quad \\ \mathrm{E}\left[\boldsymbol{W}_{k} \boldsymbol{V}_{j}^{\mathrm{T}}\right]=\mathbf{0}\end{array}\right.
⎩
⎨
⎧E[Wk]=0,E[Vk]=0,E[WkVjT]=0E[WkWjT]=sN−k+1Qkδkjj,k≤NE[VkVjT]=sN−kRkδkj
其中:渐消因子
s
≥
1
s \ge 1
s≥1,等于
1
1
1 时与普通的Kalman滤波相同。现在是
N
N
N 时刻,
k
k
k 越小就是越以前,
s
N
−
k
s^{N-k}
sN−k 越大,噪声前面乘的系数就越大,越以前的量测和系统越不可靠,慢慢遗忘;
k
=
N
k = N
k=N 就是现在,此时
s
N
−
k
s^{N-k}
sN−k 为
1
1
1。
加了
s
s
s 之后模型还是满足Kalman滤波条件,噪声还是高斯白噪声,只是时变了,在
N
N
N 时刻的Kalman滤波如下,其实就是多了
s
s
s :
{
X
^
k
/
k
−
1
N
=
Φ
k
/
k
−
1
X
^
k
−
1
N
P
k
/
k
−
1
N
=
Φ
k
/
k
−
1
P
k
−
1
N
Φ
k
/
k
−
1
T
+
Γ
k
−
1
s
N
−
k
Q
k
−
1
Γ
k
−
1
T
K
k
N
=
P
k
/
k
−
1
N
H
k
T
(
H
k
P
k
/
k
−
1
N
H
k
T
+
s
N
−
k
R
k
)
−
1
X
^
k
N
=
X
^
k
/
k
−
1
N
+
K
k
N
(
Z
k
−
H
k
X
^
k
/
k
−
1
N
)
P
k
N
=
(
I
−
K
k
N
H
k
)
P
k
/
k
−
1
N
\left\{\begin{array}{l}\hat{\boldsymbol{X}}_{k / k-1}^{N}=\boldsymbol{\Phi}_{k / k-1} \hat{\boldsymbol{X}}_{k-1}^{N} \\ \boldsymbol{P}_{k / k-1}^{N}=\boldsymbol{\Phi}_{k / k-1} \boldsymbol{P}_{k-1}^{N} \boldsymbol{\Phi}_{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}_{k-1} {\color{green}s^{N-k}}\boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} \\ \boldsymbol{K}_{k}^{N}=\boldsymbol{P}_{k / k-1}^{N} \boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1}^{N} \boldsymbol{H}_{k}^{\mathrm{T}}+{\color{green}s^{N-k}} \boldsymbol{R}_{k}\right)^{-1} \\ \hat{\boldsymbol{X}}_{k}^{N}=\hat{\boldsymbol{X}}_{k / k-1}^{N}+\boldsymbol{K}_{k}^{N}\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k / k-1}^{N}\right) \\ \boldsymbol{P}_{k}^{N}=\left(\boldsymbol{I}-\boldsymbol{K}_{k}^{N} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k / k-1}^{N}\end{array}\right.
⎩
⎨
⎧X^k/k−1N=Φk/k−1X^k−1NPk/k−1N=Φk/k−1Pk−1NΦk/k−1T+Γk−1sN−kQk−1Γk−1TKkN=Pk/k−1NHkT(HkPk/k−1NHkT+sN−kRk)−1X^kN=X^k/k−1N+KkN(Zk−HkX^k/k−1N)PkN=(I−KkNHk)Pk/k−1N
增益计算回路改写
提取出
s
N
k
s^{N_k}
sNk
s
−
(
N
−
k
)
P
k
/
k
−
1
N
=
Φ
k
/
k
−
1
s
⋅
s
−
[
N
−
(
k
−
1
)
]
P
k
−
1
N
Φ
k
/
k
−
1
T
+
Γ
k
−
1
Q
k
−
1
Γ
k
−
1
T
K
k
N
=
s
−
(
N
−
k
)
P
k
∣
k
−
1
N
H
k
T
(
H
k
s
−
(
N
−
k
)
P
k
k
k
−
1
N
H
k
T
+
R
k
)
−
1
s
−
(
N
−
k
)
P
k
N
=
(
I
−
K
k
N
H
k
)
s
−
(
N
−
k
)
P
k
∣
k
−
1
N
\begin{array}{l} {\color{red}s^{-(N-k)} \boldsymbol{P}_{k / k-1}^{N}}=\boldsymbol{\Phi}_{k / k-1} {\color{green}s} \cdot {\color{red}s^{-[N-(k-1)]} \boldsymbol{P}_{k-1}^{N}} \boldsymbol{\Phi}_{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} \\ \boldsymbol{K}_{k}^{N}={\color{red}s^{-(N-k)} \boldsymbol{P}_{k \mid k-1}^{N}}\boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} {\color{red}s^{-(N-k)} \boldsymbol{P}_{k k k-1}^{N}} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1} \\ {\color{red}{s^{-(N-k)} \boldsymbol{P}_{k}^{N}}}=\left(\boldsymbol{I}-\boldsymbol{K}_{k}^{N} \boldsymbol{H}_{k}\right) s^{-(N-k)} \boldsymbol{P}_{k \mid k-1}^{N} \\ \end{array}
s−(N−k)Pk/k−1N=Φk/k−1s⋅s−[N−(k−1)]Pk−1NΦk/k−1T+Γk−1Qk−1Γk−1TKkN=s−(N−k)Pk∣k−1NHkT(Hks−(N−k)Pkkk−1NHkT+Rk)−1s−(N−k)PkN=(I−KkNHk)s−(N−k)Pk∣k−1N
将红色部分合并:令
P
k
∗
≜
s
−
(
N
−
k
)
P
k
N
,
P
k
/
k
−
1
∗
≜
s
−
(
N
−
k
)
P
k
/
k
−
1
N
\boldsymbol{P}_{k}^{*} \triangleq s^{-(N-k)} \boldsymbol{P}_{k}^{N}, \boldsymbol{P}_{k / k-1}^{*} \triangleq s^{-(N-k)} \boldsymbol{P}_{k / k-1}^{N}
Pk∗≜s−(N−k)PkN,Pk/k−1∗≜s−(N−k)Pk/k−1N ,得
{
X
^
k
/
k
−
1
∗
=
Φ
k
/
k
−
1
X
^
k
−
1
∗
P
k
/
k
−
1
∗
=
Φ
k
/
k
−
1
(
s
P
k
−
1
∗
)
Φ
k
/
k
−
1
T
+
Γ
k
−
1
Q
k
−
1
Γ
k
−
1
T
K
k
∗
=
P
k
/
k
−
1
∗
H
k
T
(
H
k
P
k
/
k
−
1
∗
H
k
T
+
R
k
)
−
1
X
^
k
∗
=
X
^
k
/
k
−
1
∗
+
K
k
∗
(
Z
k
−
H
k
X
^
k
/
k
−
1
∗
)
P
k
∗
=
(
I
−
K
k
∗
H
k
)
P
k
/
k
−
1
∗
\left\{\begin{array}{l}\hat{\boldsymbol{X}}_{k / k-1}^{*}=\boldsymbol{\Phi}_{k / k-1} \hat{\boldsymbol{X}}_{k-1}^{*} \\ \boldsymbol{P}_{k / k-1}^{*}=\boldsymbol{\Phi}_{k / k-1}\left({\color{green}s} \boldsymbol{P}_{k-1}^{*}\right) \boldsymbol{\Phi}_{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} \\ \boldsymbol{K}_{k}^{*}=\boldsymbol{P}_{k / k-1}^{*} \boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1}^{*} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1} \\ \hat{\boldsymbol{X}}_{k}^{*}=\hat{\boldsymbol{X}}_{k / k-1}^{*}+\boldsymbol{K}_{k}^{*}\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k / k-1}^{*}\right) \\ \boldsymbol{P}_{k}^{*}=\left(\boldsymbol{I}-\boldsymbol{K}_{k}^{*} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k / k-1}^{*}\end{array}\right.
⎩
⎨
⎧X^k/k−1∗=Φk/k−1X^k−1∗Pk/k−1∗=Φk/k−1(sPk−1∗)Φk/k−1T+Γk−1Qk−1Γk−1TKk∗=Pk/k−1∗HkT(HkPk/k−1∗HkT+Rk)−1X^k∗=X^k/k−1∗+Kk∗(Zk−HkX^k/k−1∗)Pk∗=(I−Kk∗Hk)Pk/k−1∗
改写的式子中就只有一个
s
s
s ,用起来很简单,对上一时刻的
P
P
P 阵乘以一个标量
s
s
s 就行。
遗忘效果的理解
s s s 取值越大,对以前信息的利用更小