直接导入无图片，先不改了，不过图片都是原题目，不影响对答案。

计算机系统2022期末

本课程的复习请以知识点复习为重，全部内容共有大小280+个知识点，都可能在期末考试出现，仅通过往年试卷复习是远远不够的，往年试卷仅能作为部分知识点的检测以及题目类型的大致参考，复习本课程需要尽可能完整复习所学的知识点，串联各个章节关联的部分。

本答案非标准答案，是我本学期完成的。由于对全部知识点已经没有一年前熟悉，请几位同学完成了部分题目进行了核验，但是最后一题由于课程未结束，没有请同学做并和我核对，有任何问题请及时私戳我。

作为检验复习情况的参考：本卷整体简单(前六题)，涉及的知识点较少，复习之后应该顺利完成。完成该卷的时长超过2h是正常的，2h应该可以完成前六题+最后一题的读题(快的话可以做一部分了)。不用担心题量问题，如果考试遇到了难度比较大且难以完成的题，保证其他题正确就足够了。最后一题难度稍大，我写明了完整的地址翻译过程给大家参考，理解整个地址翻译过程是很重要的，如果弄明白最后一题，任何形式的对地址翻译的考察就都没有问题了。

根据几个同学做题的情况，第4题也比较容易出错，难度略大于其他题，请同学们注意，复习好最基本的汇编指令都完成了什么动作，避免在基础题上犯错。

1.IEEE浮点数

(1)证明：

IEEE浮点数表示为：
$n=(-1)^s \times M \times 2^E$
阶码部分为：
$\begin{cases} e- bias & 规格化数\\ 1-bias &非规格化数 \end{cases}$
题设范围内，不存在负数和特殊值。符号位为0，因此编码可只考虑后31位。若m<n，则：
$M_m\times 2^{E_m}<M_n\times 2^{E_n}$

若Em=En，满足上式必须有Mm<Mn，则m与n的阶码部分编码相同，尾数部分m<n，有fm<fn
若Em<En，Mm和Mn可能取任意值：
- m和n都是规格化数：E=e-bias，em<en，编码的高位m<n，fm<fn
- m是规格化数，n是非规格化数：不存在这种情况，规格化数m<非规格化数n
- m是非规格化数，n是规格化数：em(全0)<en，编码的高位m<n，fm<fn

|说明：

本题不需要严格的证明，列出浮点数表示，分情况讨论就可以了，并且有以上两点就可以了。Em>En的情况，不存在m<n，不便也不需证明或说明。从下图可以看出，阶码大的数值总是更大：

(2)证明：

假设m+1，n+1也都是规格化数，则有：
$step_m=m+1-m=2^{E_m}(M_m+1-M_m)=2^{E_m} \\ step_n=n+1-n=2^{E_n}(M_n+1-M_n)=2^{E_n}$
由m<n，Em<=En，即stepm<=stepn。

假设m为非规格化数，m+1为规格化数，stepm=1。(由于非规格化数阶码为1-bias，规格化数为E-bias，二者之间实现了平滑的过渡，可参照上表)。此时也有stepm<=stepn，无论n+1和n的具体情况。

|说明：

本题同样不需要严格的证明，分情况简要说明即可。

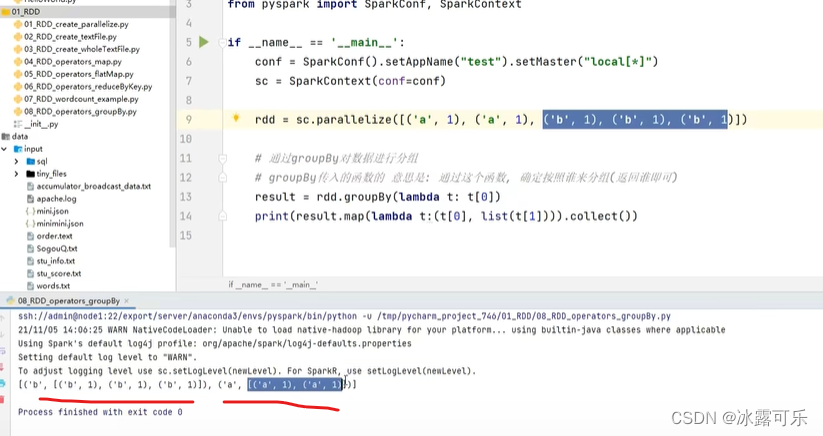
2.汇编代码分析

(1)

(2)

(3)

(j>15) ? 0 : (j-15)

(4)

array1[i][j] - 2array2[k]

(5)

sum + array1[0][0] + array2[0]

3.汇编代码分析

(1)

*x>a[y]

(2)

xy>ua.i

(3)

test1(ua.pi, test1(ua.pi, ua.i+10))

|说明：

ua.pi、ua.i直接写为ua也正确，但是源程序中应该是写全的。本题和上题较为简单，应该保证可以无误完成。

4.汇编程序模拟

(1)

帧栈变化过程如下：

	esp	ebp
进入main函数，调整栈指针	0xbffff1e0	0xbffff1f8
call P(5)，retaddr入栈	0xbffff1dc	0xbffff1f8
控制转移给P(5)，调整栈指针	0xbffff1c0	0xbffff1d8
call P(16)，retaddr入栈	0xbffff1bc	0xbffff1d8
控制转移给P(8)，调整栈指针	0xbffff1a0	0xbffff1b8
call P(8)，retaddr入栈	0xbffff19c	0xbffff1b8
控制转移给P(8)，调整栈指针	0xbffff180	0xbffff198
call P(4)，retaddr入栈(题中所求位置)	0xbffff17c	0xbffff198
控制转移给P(4)，调整栈指针	0xbffff160	0xbffff178

题中所求位置，刚刚执行完call P(4)，(%esp)为返回地址0x804842f，(%esp+4)为参数4。

|说明：

本题考察程序执行过程中栈和栈指针的变化，细心模拟就可以完成，但是可能需要一点时间，不要忘记CALL指令让返回地址入栈，改变栈指针。

(2)

更改后的程序：

void p(int x){
    cout<<x<<endl;
    while(x>1){
        if(x%2==0) x/=2;
        else x=x*3+1;
    }
}

递归函数每次调用自身时都会重新开辟栈空间，当递归调用次数过多时，就会因栈空间耗尽而导致段错误。修改为非递归情况后，处理过程中只对固定位置的x的值进行修改，就不会出现栈空间耗尽的问题。

5.CPU设计题

(1)

增加的部分：

(2)

添加寄存器B。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FccWNcGJ-1686106724904)(2022期末/image-20230512101623027.png)]

|说明：

本题只需要照着原状态和数据通路补充就可以了，如果遇到已出现的同类型指令的CPU设计问题，应该能快速解决。

6.链接与异常控制流

(1)

可执行目标文件没有.rel节。.rel节存放了可重定位条目，用于链接时的重定位，链接完成后的可执行目标文件不再需要该节。
可执行目标文件中的节经重定位后，都已经有了最终的运行时存储器地址。链接器进行重定位时，会将可重定位目标文件中所有相同类型的节合并为同一类型的新的聚合节，并将运行时存储器地址赋给新的聚合节和每个符号，并完成了节中符号引用的重定位。
可执行目标文件有一个.init节，在程序加载后会调用该节代码进行初始化。

(2)

该段代码在符号解析时存在多重定义问题。对于变量x，函数f存在多重定义。函数和已经初始化的全局变量是强符号，未初始化的全局变量是弱符号。多重定义的符号按照以下规则来处理：

不允许多个强符号
一个强符号和多个弱符号，选择强符号
如果有多个弱符号，任意选择一个

该段代码的两个x的定义均为弱符号，会随机选择一个定义。而f有一个强符号定义，会采用为x赋值的f函数。运行时，可能x选择了int型，占4个字节，而f按照double类型对x进行8字节赋值，会覆盖存储器中x和y的位置。

(3)

重定位分为两步：

重定位节和符号定义：链接器将所有相同类型的节合并为同一类型的新的聚合节，将运行时存储器地址赋给新的聚合节，赋给每个符号，此时所有的指令和全局变量都有唯一的运行时存储器地址。
重定位节中的符号引用：链接器修改代码和数据节中对每个符号的引用，使这些引用指向正确的运行时地址。该步需要借助重定位条目完成。

(4)

在输入可执行文件名之后，shell会通过execve函数调用加载器，修改虚拟地址空间，在可执行目标文件的段头部表的指导下将文件的代码和数据段拷贝到存储器中，然后跳转到程序入口_start，调用一些初始化例程，并调用atexit例程注册一些终止时调用的程序。接着调用main函数，运行结束后，会调用_exit函数，终止程序，将控制返回操作系统。

(5)

会产生SIGCHLD信号，发送给父进程，信号的接收者是shell，表示子进程已经停止或终止。信号不排队指的是同一类型的信号，最多有一个处于待处理状态，后续到来的相同信号会被直接丢弃。这是因为待处理信号是用位向量维护的，不能计数。

|说明：

本题都是基本的概念，其中(1)只需要答出两点，应该至少可以答出前两点，其他问内容本身就很少，尽量答全。

7.虚拟存储器+存储器层次结构

为了加快地址翻译，使用TLB进行地址缓存，如果TLB命中，则得到PDE，计算出页表的物理地址，然后找到PTE，完成地址的翻译。由图可以看出，TLB采用四路组相联，因此查找过程为先由索引找到组，再匹配tag进行查找。TLB是用VPN的位进行索引的，本题中页是4K的，偏移量VPO占用了12位，因此前20位用于TLB查找，需要先将地址进行划分，这20位中，组索引是后2位，tag是前18位。

如果未命中，则需要到物理存储中找到PDE，PDE的地址是页目录的基址0x45d000，偏移是虚拟地址的前10位。偏移量需要左移2位，因为一个PDE4字节，类似于数组寻址，A[i]的地址是A+4i。页表同理。从PDE得到的二级页表基址还要左移12位，因为二级页表有4KB，基址后12位为0。

该题中TLB直接缓存了物理页号，而在书中，TLB缓存的是PTE。注意这个区别。