一、基本数学运算

● max（a，b）
○ 返回较大的
● min（a，b）
○ 返回较小的
● mul（a，b）
○ 两向量相乘，常用于矩阵运算
● abs（a）
○ 返回a的绝对值
● round（x）
○ 返回与x最近的整数
● sqrt（x）
○ 返回x的平方根
● rsqrt（x）
○ 返回x的平方根的倒数
● degrees（x）
○ 将弧度转化为角度
● redians（x）
○ 将角度转化为弧度
● noise（x）
○ 噪声函数
○ 将uv的坐标作为x传入，随机的返回一个[0,1]的值，就会得到一张噪声图
在这里插入图片描述

二、幂指对函数与偏导数

● pow（x，y）
○ x的y次幂（x、y都可以是自变量或具体数） → $x^y$
● exp（x）
○ 返回以e为底的指数函数 → $e^x$
● exp2（value x）
○ 返回以2为底，x为指数的幂 → $2^x$
● ldexp（x，exp）
○ 返回与2的exp次方的乘积 → $x*2^exp$
● log（x）
○ 返回指定值的以e为底数的对数 → $l n x$
● log10（x）
○ 求以10为底的对数 → $log_{10}x$
● log2（x）
○ 求以2为底数的对数 → $log_{2}x$
● frexp（x，out exp）
○ 把浮点数分解为尾数和指数，x的返回值是尾数（x=ret*2^exp），exp参数返回的是指数
○ 是按照计算机存储浮点数的方式分解的
■ eg：1.2这个数，是分为两部分的，尾数为12，指数为0.1
○ out关键字：exp也会作为一个返回值传出，也就是说这个函数有两个返回值。
○ 如果x参数为0，则此函数的尾数和指数均返回0

三、三角函数和双曲线函数

● sin（x）、cos（x）、tan（x）
○ 三角函数（弧度制：1°=π/180 rad）
● asin（x）、acos（x）、atan（x）
○ 反三角函数
● sincos（x，out s，out c）
○ 返回x的正弦和余弦
● tan（y，x）
○ 返回y/x的正切
● atan2（y，x）
○ 返回y/x的反正切
● 双曲正余弦
○ sinh（x）返回x的双曲正弦值 → $e^{x}-e^{-x}）/2$
○ cosh（x）返回x的双曲余弦值 → $e^{x}+e^{-x}）/2$
○ tanh（x）返回x的双曲正弦值 → $e^{x}-e^{-x}）/（e^{x}+e^{-x}）$

四、数据范围类

● ceil（x）
○ 返回>=x的最小整数（向上取整）
● floor（x）
○ 返回<=x的最大整数（向下取整）
● step（x，y）
○ x<=y返回1（真），否则返回0
● saturate（x）
○ 返回将x钳制到[0,1]范围之间的值
● clamp（x，min，max）
○ 将x限制在[min，max]范围的值，比min小返回min，比max大返回max
● fmod（x，y）
○ 返回x对y取余的余数
● frac（x）
○ 取x的小数部分
● modf（x，out ip）
○ 将x分为小数和整数部分（输出的ip为整数部分，返回值为小数部分）
● lerp（x，y，s）
○ 按照s在x到y之间插值，返回 $x * （ 1 - s ） + y * s$
● smoothstep（min，max，x）
○ 如果x在[min，max]范围内，就返回介于[0，1]之间的平滑Hermite插值，使用smoothstep在两个值直接创建平滑过渡
○ 平滑地混合两种颜色

五、类型判断类

● all（x）
○ 确定指定量的所有分量是否均为非零，均非零则返回true，否则返回false（处理由浮点型、整型、布尔型数据定义的标量、向量或者矩阵）
● clip（x）
○ 如果输入值小于零，则丢弃当前像素常用于判定范围(不仅仅针对0,返回值为void)
○ 常用于Alpha Test，如果每个分量代表到平面的距离，还可以用来模拟剪切平面
● sign（x）返回x的正负性
○ 如果x小于零返回-1
○ 如果x等于零返回0
○ 如果x大于零返回1
● isinf（x）
○ 如果x参数为+ INF或-INF(无穷+无穷仍无穷，0x3f3f3f3f)，返回true，否则返回False
● isfinite（x）
○ 判断x参数是有限，即有界的，与isinf(x)相反
● isnan（x）
○ 如果x参数为NAN(非数字)，返回true，否则返回false

六、向量和矩阵类

● length(v)
○ 返回向量的长度
● normalize(v)
○ 向量归一化，x/length(x) 方向向量归一化
● distance(a,b)
○ 返回两个向量之间的距离，不平行的两个向量应该为0，此处表示为根号下各分量之差的平方和
● dot(a,b)
○ 点积
● cross(a,b)
○ 叉积
● determinant(m)
○ 返回指定浮点矩阵的按行列式方式计算的值
● transpose(m)
○ 返回矩阵m的转置矩阵

七、光线运算类

● reflect(i,n)
○ 以i为入射向量n为法线方向的反射光
● refract(i,n,ri)
○ 以i为入射向量n为法线方向,ri为折射率的折射光
● lit(n_dot_l,n_dot_h，m)
○ 输入标量(normal,light,半角向量h,镜面反射系数m)
○ 返回光照向量(环境光，漫反射光，镜面高光反射，1)

八、纹理查找

1.一些注意的点：
纹理查找的分类
● 所有的纹理查找函数都可以分为三类：普通的、微分的、投影的

—1.1 偏导函数ddx ddy（微分类）
● 如果函数 ddx 的参数为 myVar，该参数对应的像素点记为p（i，j），则 ddx(myVar)的值为“像素点 p（i+1，j）的值减去myVar”（ddy同理）
● 如果函数 ddx 和 ddy 的输入参数为常数，则函数返回值永远为 0。
● 1.函数 ddx 和 ddy 用于求取相邻像素间某属性的差值；
● 2.函数 ddx 和 ddy 的输入参数通常是纹理坐标；
● 3.函数 ddx 和 ddy 返回相邻像素键的属性差值；偏导数的物理含义是：在某一个方向上的变化快慢。
○ 4 所以 ddx 求的是 X 方向上，相邻两个像素的某属性值的变化量
○ 5 ddy 求的是 Y方向上，相邻两个像素的某属性值的变化量
● 6 由于 ddx 和 ddy 指令是作用于像素级的，所以 ddx 和 ddy 函数只被片段程序所支持
● mipmap在选择到底用哪一层mipmap的level时，靠的就是偏导数。

1.2 投影类
● 投影纹理是指：将纹理当做一张幻灯片投影到场景中，使用投影纹理技术需要计算投影纹理坐标，然后使用投影纹理坐标进行查询。使用投影纹理坐
标进行查询的函数就是投影纹理查询函数。

1.3 Mipmap类
● lod 采样一张mipmap
● bias 偏置后再采样（由t，w决定）
● grad 使用微分来选择mip的层，进行采样

1D纹理查找（几乎不用）
● tex1D(s, t) 普通一维纹理查找返回纹理采样器s在标量t位置的color4
● tex1D(s,t,ddx,ddy) 使用微分查询一维纹理， t和ddxy均为vector
● tex1Dlod(s, t) 使用LOD查找纹理s在t.w位置的color4
● tex1Dbias(s, t) 将t.w决定的某个MIP层偏置后的一维纹理查找
● tex1Dgrad(s,t,ddx,ddy) 使用微分并指定MIP层的一维纹理查找
● ex1Dproj(s, t) 把纹理当做一张幻灯片投影到场景中，先使用投影纹理技术需要计算出投影纹理坐标t(坐标t.w除以透视值)，然后使用投影纹理坐标进行查询

2D纹理查找
● tex2D(s, t) 普通二维纹理查找返回纹理采样器s在vector t位置的颜色
● tex2D(s,t,ddx,ddy) 使用微分查询二维纹理，t和ddxy均为vector
● tex2Dlod(s, t) 使用LOD查找纹理s在t.w位置的color4
● tex2Dbias(s, t) 将t.w决定的某个MIP层偏置后的二维纹理查找
● tex2Dgrad(s,t,ddx,ddy) 使用微分并指定MIP层的二维纹理查找
● tex2Dproj(s, t) 把纹理当做一张幻灯片投影到场景中，先使用投影纹理技术需要计算出投影纹理坐标t(坐标t.w除以透视值)，然后使用投影纹理坐标进行查询

3D纹理查找
● tex3D(s, t) 普通三维纹理查找返回纹理采样器s在vector t位置的颜色
● tex3D(s,t,ddx,ddy) 使用微分查询三维纹理， t和ddxy均为vector
● tex3Dlod(s, t) 使用LOD查找纹理s在t.w位置的color4
● tex3Dbias(s, t) 将t.w决定的某个MIP层偏置后的三维纹理查找
● tex3Dgrad(s,t,ddx,ddy) 使用微分并指定MIP层的三维纹理查找
● tex3Dproj(s, t) 把纹理当做一张幻灯片投影到场景中，先使用投影纹理技术需要计算出投影纹理坐标t(坐标t.w除以透视值)，然后使用投影纹理坐标进行查询

立方体纹理查找
立方体体纹理记录三个方向，从里到外的信息
● texCUBE(s,t) 返回纹理采样器s在vector t位置的颜色
● texCUBE(s,t,ddx,ddy) 使用微分查询立方体维纹理，t和ddxy均为vector
● texCUBEDload(s,t) 使用LOD查找纹理s在t.w位置的color4
● texCUBEbias(s,t) 将t.w决定的某个MIP层偏置后的立方体纹理查找
● texCUBEgrad(s,t,ddx,ddy) 使用微分并指定MIP层的立方体纹理查找
● texCUBEproj(s,t) 使用投影方式的立方体纹理查找

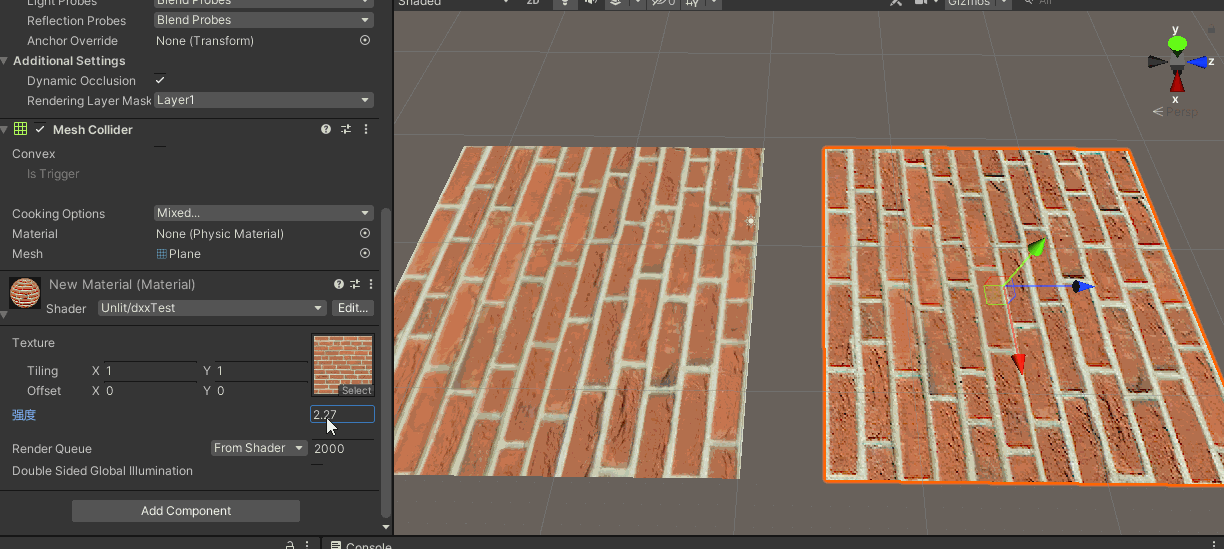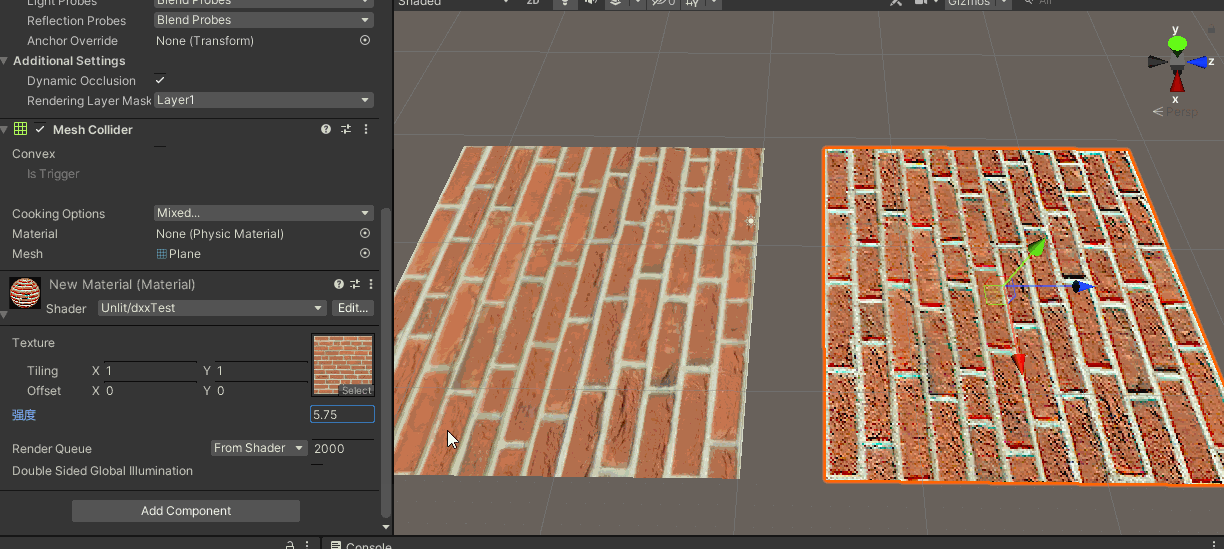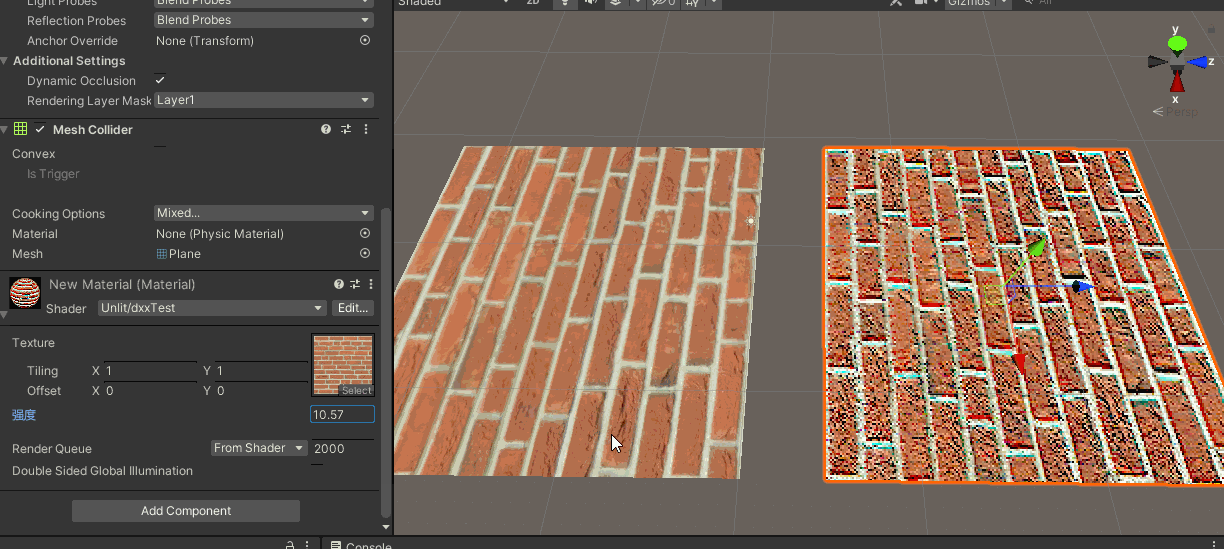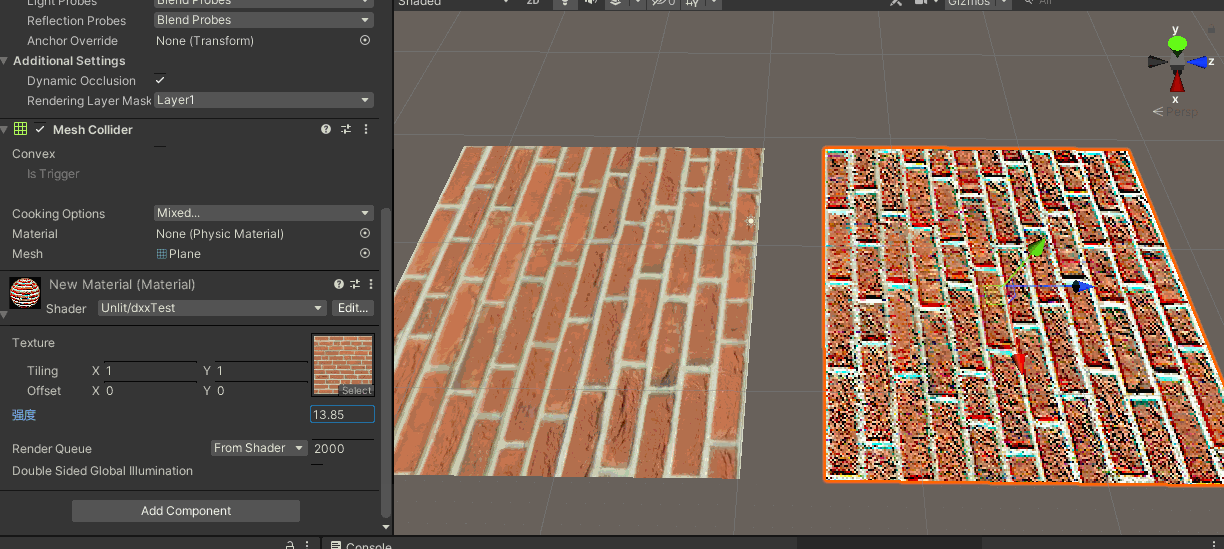
2.ddx ddy的实际使用测试

● 上边说了，ddx 、ddy求的是 x、y方向上，相邻两个像素的某属性值的变化量
● 这也就是《GAMES101》中讲mipmap部分时说的，相邻像素（pixel）之间的距离（差值）对应到纹理（texel）中是多少距离。
● 随便找个了采样贴图的shader，左边为正常采样的结果，作为对照
● 右边部分，shader中声明一个修改差值的系数Range，并在片元着色器中添加ddx ddy的部分。

   fixed4 frag (v2f i) : SV_Target
            {
                // sample the texture
                fixed4 col = tex2D(_MainTex, i.uv);
                col += (ddx(col), ddy(col)) * _Float;
                // apply fog
                // UNITY_APPLY_FOG(i.fogCoord, col);
                return fixed4(col.rgb,1.0);
            }