一. 关于关键路径

1. 有向无环图

2. AOV网

3. 拓补排序

4. 关键路径

二. 如何实现寻找关键路径

三. 关键路径的代码实现

1. 正向计算

1.1 计算每个节点的入度

1.2 拓扑排序（计算每个节点最早开始的时间）

2. 反向计算

2.1 计算每个节点的出度，计算方法类似1.1，这里不再赘述。

2.2 逆拓扑排序（计算每个节点最晚开始的时间）

3. 计算关键路径

四. 代码展示

五. 数据测试

六. 总结与反思

一. 关于关键路径

1. 有向无环图

若一个有向图中不存在环，则称为有向无环图，简称DAG图。

2. AOV网

若用DAG图表示一个工程，其顶点表示活动，用有向边< $V_{i},V_{j}$ > 表示活动 $V_{i}$ 必须先于活动 $V_{j}$ 进行的这样一种关系，则将这种有向图称为顶点表示活动的网格，记为AOV网。在AOV网中，活动 $V_{i}$ 是活动 $V_{j}$ 的直接前驱，活动 $V_{j}$ 是活动 $V_{i}$ 的直接后继，这种前驱关系和后继关系具有传递性，且任何活动 $V_{i}$ 不能以它自己作为自己的前驱或后继。

3. 拓补排序

在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件时，称为该图的一个拓扑排序。

①每个顶点出现且只出现一次。

②若顶点A在序列中排在顶点B的前面，则在图中不存在从顶点B到顶点A的路径，或定义为：拓扑排序是对有向无环图的顶点的一种排序，它使得若存在一条从顶点A到顶点B的路径，则在排序中顶点B出现在顶点A的后面。每个AOV网都有一个或多个拓扑排序序列。

对一个AOV网进行拓扑排序的算法有很多，下面介绍比较常用的一种方法的步骤：

从AOV网中选择一个没有前驱的顶点输出；从网中删除该顶点和所有以它为起点的有向边；重复前面上述两步直到当前的AOV网为空或当前网中不存在无前驱的顶点为止。

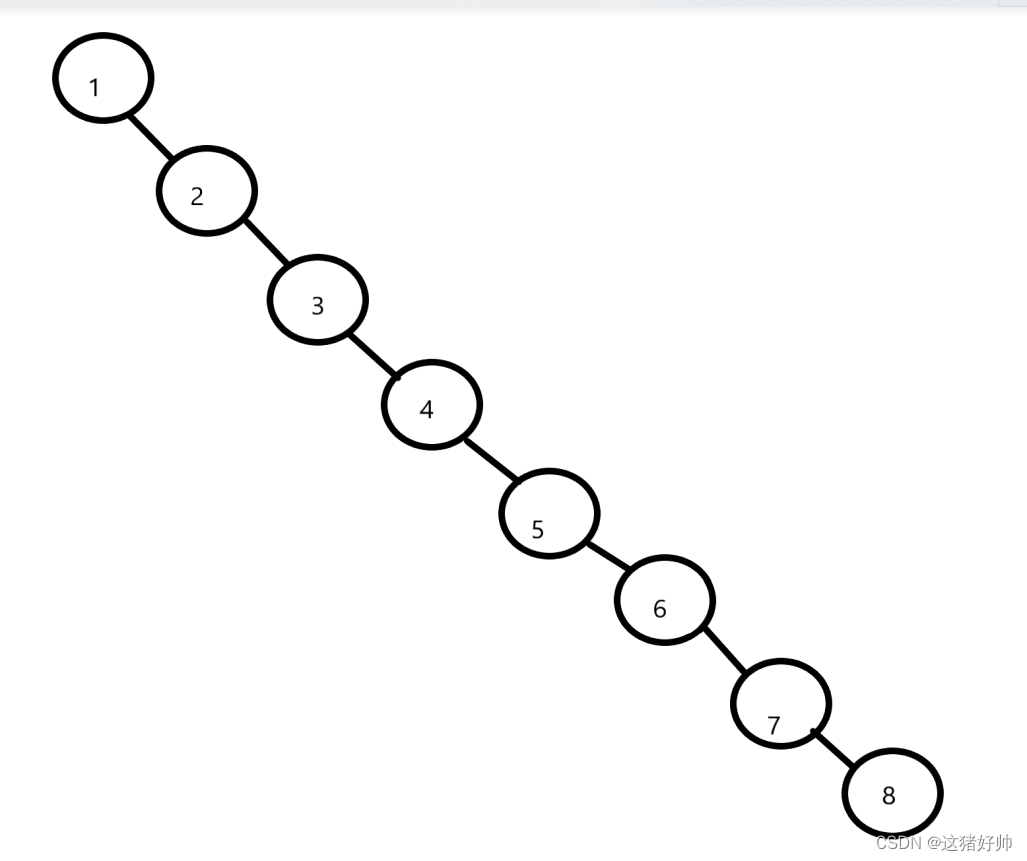
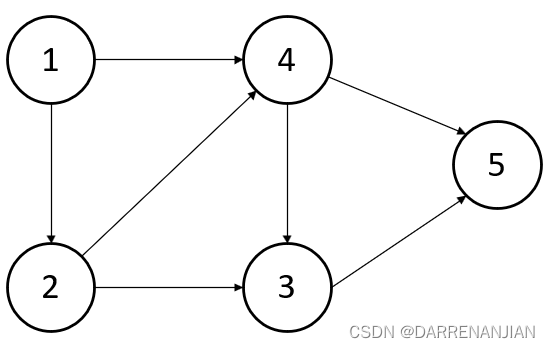
图G1-G6为拓扑排序过程的示例

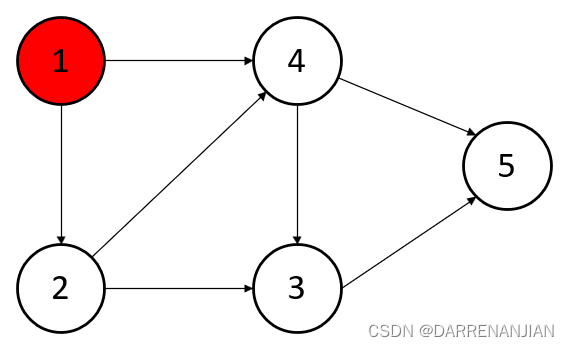
第一步找到节点1的入度为0，输出1，并且删除与节点1直接相连的有向边

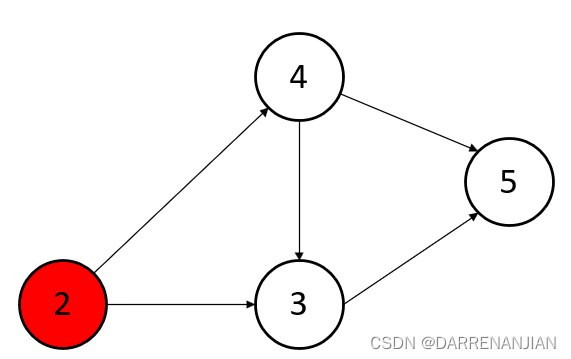
第二步找到节点2的入度为0，输出2，并且删除与节点2直接相连的有向边

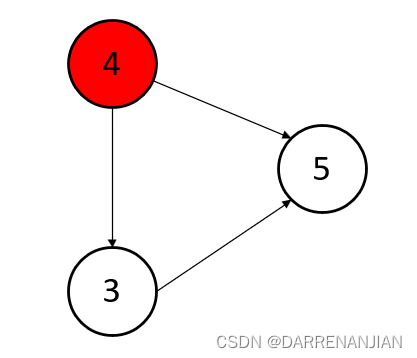
第三步找到节点3的入度为0，输出3，并且删除与节点3直接相连的有向边

第四步找到节点4的入度为0，输出4，并且删除与节点4直接相连的有向边

第五步找到节点5的入度为0，输出5。

4. 关键路径

在带权有向图中，以顶点表示事件，以有向边表示活动，以边上的权值表示完成该活动的开销(如完成活动所需的时间)，称之为用边表示活动的网络，简称AOE网。AOE网和AOV网都是有向无环图，不同之处在于它们的边和顶点所代表的含义是不同的，AOE网中的边有权值；而AOV网中的边无权值，仅表示顶点之间的前后关系。

         AOE网具有以下两个性质：
        ①只有在某顶点所代表的事件发生后，从该顶点出发的各有向边所代表的活动才能开始；
        ②只有在进入某顶点的各有向边所代表的活动都已结束时，该顶点所代表的事件才能发生。

在AOE网中仅有一个入度为0的顶点，称为开始顶点(源点)，它表示整个工程的开始；网中也仅存在一个出度为0的顶点，称为结束顶点(汇点)，它表示整个工程的结束。在AOE网中，有些活动是可以并行进行的。从源点到汇点的有向路径可能有多条，并且这些路径长度可能不同。完成不同路径上的活动所需的时间虽然不同，但是只有所有路径上的活动都已完成，整个工程才能算结束。因此，从源点到汇点的所有路径中，具有最大路径长度的路径称为关键路径，而把关键路径上的活动称为关键活动。

完成整个工程的最短时间就是关键路径的长度，即关键路径上各活动花费开销的总和。这是因为关键活动影响了整个工程的时间，即若关键活动不能按时完成，则整个工程的完成时间就会延长。因此，只要找到了关键活动，就找到了关键路径，也就可以得出最短完成时间。

二. 如何实现寻找关键路径

现解释符号：事件 $V_{k}$ 的最早发生时间 $V_{ek}$ ，事件 $V_{k}$ 的最晚发生时间 $V_{lk}$

求关键路径的算法步骤如下：

step1：从源点出发，令 $V_{eStart}$ =0，按拓扑有序求其余顶点的最早发生时间 $V_{ek}$ ；

step2：从汇点出发，令 $V_{lLast}$ = $V_{eLast}$ ，按拓扑有序求其预定点的最迟发生时间 $V_{lk}$ ；

step3：根据各顶点的 $V_{ek}$ 和 $V_{lk}$ 的差值为0，计算出关键路径的节点，即这些顶点构成关键路径。

三. 关键路径的代码实现

1. 正向计算

1.1 计算每个节点的入度

根据第i行邻接矩阵不为-1的列的个数，计算第i个节点的入度，得到的结果存储在矩阵tempInDegrees里面。

        // Step 1. The in-degree of each node.
        int[] tempInDegrees = new int[numNodes];
        for (int i = 0; i < numNodes; i++) {
            for (int j = 0; j < numNodes; j++) {
                if (weightMatrix.getValue(i, j) != -1) {
                    tempInDegrees[j]++;
                } // Of if
            } // Of for j
        } // Of for i
        System.out.println("In-degree of nodes: " + Arrays.toString(tempInDegrees));

1.2 拓扑排序（计算每个节点最早开始的时间）

首先初始化设置每一个节点最早开始的时间都为0，用矩阵tempEarliestTimeArray记录。接着从节点0开始循环，找到入度为0的节点j，移出节点j，更新图中剩余节点的信息：若邻接矩阵第0行的第j列不为-1（0号节点与j号节点连通），计算tempValue= 0号节点最早开始时间tempEarliestTimeArray[0] +节点0到节点j的时间；若tempValue计算得到的结果大于tempEarliestTimeArray[j]（j号节点最早能多久开始），那么更新tempEarliestTimeArray[j]=tempValue（保证节点j最早能够开始的时间一定是路径里面最大的，否则就是节点j在条件没有满足的情况下开始（不符合题意）），将j号节点的入度tempInDegrees[j]减1；继续找入度为0的节点i，按照上述计算；当0号节点循环完成（第一个入度为0）。接着寻找第二个入度为0的节点k按照0号节点一样对计算方法，得到计算结果...最终我们得到所有节点最早开始的矩阵tempEarliestTimeArray。

        // Step 2. Topology sorting.
        int[] tempEarliestTimeArray = new int[numNodes];
        for (int i = 0; i < numNodes; i++) {
            // This node cannot be removed.
            if (tempInDegrees[i] > 0) {
                continue;
            } // Of if

            System.out.println("Removing " + i);

            for (int j = 0; j < numNodes; j++) {
                if (weightMatrix.getValue(i, j) != -1) {
                    tempValue = tempEarliestTimeArray[i] + weightMatrix.getValue(i, j);
                    if (tempEarliestTimeArray[j] < tempValue) {
                        tempEarliestTimeArray[j] = tempValue;
                    } // Of if
                    tempInDegrees[j]--;
                } // Of if
            } // Of for j
        } // Of for i

        System.out.println("Earlest start time: " + Arrays.toString(tempEarliestTimeArray));

2. 反向计算

2.1 计算每个节点的出度，计算方法类似1.1，这里不再赘述。

        // Step 3. The out-degree of each node.
        int[] tempOutDegrees = new int[numNodes];
        for (int i = 0; i < numNodes; i++) {
            for (int j = 0; j < numNodes; j++) {
                if (weightMatrix.getValue(i, j) != -1) {
                    tempOutDegrees[i]++;
                } // Of if
            } // Of for j
        } // Of for i
        System.out.println("Out-degree of nodes: " + Arrays.toString(tempOutDegrees));

2.2 逆拓扑排序（计算每个节点最晚开始的时间）

用矩阵tempLatestTimeArray记录每个节点最晚开始的时间，初始化tempLatestTimeArray都等于tempEarliestTimeArray[5]。同样的道理我们寻找出度为0的节点，第一个出度为0的节点是5。寻找节点j直接与节点5相连，若tempValue=tempLatestTimeArray[i]（节点i最迟开始时间）-节点j到节点i的时间小于tempLatestTimeArray[j]（节点j的最迟开始时间），那么更新tempLatestTimeArray[j]=tempValue。节点j的出度tempOutDegrees[j]减1。继续循环直到邻接矩阵第6行结束。最后继续寻找下一个出度为0的节点i，继续上述循环。

        // Step 4. Reverse topology sorting.
        int[] tempLatestTimeArray = new int[numNodes];
        for (int i = 0; i < numNodes; i++) {
            tempLatestTimeArray[i] = tempEarliestTimeArray[numNodes - 1];
        } // Of for i

        for (int i = numNodes - 1; i >= 0; i--) {
            // This node cannot be removed.
            if (tempOutDegrees[i] > 0) {
                continue;
            } // Of if

            System.out.println("Removing " + i);

            for (int j = 0; j < numNodes; j++) {
                if (weightMatrix.getValue(j, i) != -1) {
                    tempValue = tempLatestTimeArray[i] - weightMatrix.getValue(j, i);
                    if (tempLatestTimeArray[j] > tempValue) {
                        tempLatestTimeArray[j] = tempValue;
                    } // Of if
                    tempOutDegrees[j]--;
                    System.out.println("The out-degree of " + j + " decreases by 1.");
                } // Of if
            } // Of for j
        } // Of for i

        System.out.println("Latest start time: " + Arrays.toString(tempLatestTimeArray));

3. 计算关键路径

我们得到了两个矩阵tempEarliestTimeArray，tempLatestTimeArray，将这两个矩阵相减，得到值为0的节点，那么就是关键路径上面的节点，得到最终答案。

        boolean[] resultCriticalArray = new boolean[numNodes];
        for (int i = 0; i < numNodes; i++) {
            if (tempEarliestTimeArray[i] == tempLatestTimeArray[i]) {
                resultCriticalArray[i] = true;
            } // Of if
        } // Of for i

        System.out.println("Critical array: " + Arrays.toString(resultCriticalArray));
        System.out.print("Critical nodes: ");
        for (int i = 0; i < numNodes; i++) {
            if (resultCriticalArray[i]) {
                System.out.print(" " + i);
            } // Of if
        } // Of for i

四. 代码展示

主类：

package Day_39;
import Day_38.Net;
public class demo1 {
    /**
     *********************
     * The entrance of the program.
     *
     * @param args
     *            Not used now.
     *********************
     */
    public static void main(String args[]) {
        int MAX_DISTANCE= 1000;
//        Net tempNet0 = new Net(3);
//        System.out.println(tempNet0);
//
//        int[][] tempMatrix1 = { { 0, 9, 3, 6 }, { 5, 0, 2, 4 }, { 3, 2, 0, 1 }, { 2, 8, 7, 0 } };
//        Net tempNet1 = new Net(tempMatrix1);
//        System.out.println(tempNet1);
//
//        // Dijkstra
        tempNet1.dijkstra(1);
//
//        // An undirected net is required.
//        int[][] tempMatrix2 = { { 0, 7, MAX_DISTANCE, 5, MAX_DISTANCE }, { 7, 0, 8, 9, 7 },
//                { MAX_DISTANCE, 8, 0, MAX_DISTANCE, 5 }, { 5, 9, MAX_DISTANCE, 0, 15, },
//                { MAX_DISTANCE, 7, 5, 15, 0 } };
//        Net tempNet2 = new Net(tempMatrix2);
//        tempNet2.prim();

        // A directed net without loop is required.
        // Node cannot reach itself. It is indicated by -1.
        int[][] tempMatrix3 = { { -1, 3, 2, -1, -1, -1 }, { -1, -1, -1, 2, 3, -1 },
                { -1, -1, -1, 4, -1, 3 }, { -1, -1, -1, -1, -1, 2 }, { -1, -1, -1, -1, -1, 1 },
                { -1, -1, -1, -1, -1, -1 } };

        Net tempNet3 = new Net(tempMatrix3);
        System.out.println("-------critical path");
        tempNet3.criticalPath();
    }// Of main

}

调用类：

package Day_38;

import Day_31.IntMatrix;

import java.util.Arrays;

/**
 * Weighted graphs are called nets.
 *
 * @author An Jian 2569222191@qq.com.
 */
public class Net {

    /**
     * The maximal distance. Do not use Integer.MAX_VALUE.
     */
    public static final int MAX_DISTANCE = 10000;

    /**
     * The number of nodes.
     */
    int numNodes;

    /**
     * The weight matrix. We use int to represent weight for simplicity.
     */
    IntMatrix weightMatrix;

    /**
     * ********************
     * The first constructor.
     *
     * @param paraNumNodes The number of nodes in the graph.
     *                     ********************
     */
    public Net(int paraNumNodes) {
        numNodes = paraNumNodes;
        weightMatrix = new IntMatrix(numNodes, numNodes);
        for (int i = 0; i < numNodes; i++) {
            // For better readability, you may need to write fill() in class
            // IntMatrix.
            Arrays.fill(weightMatrix.getData()[i], MAX_DISTANCE);
        } // Of for i
    }// Of the first constructor

    /**
     * ********************
     * The second constructor.
     *
     * @param paraMatrix The data matrix.
     *                   ********************
     */
    public Net(int[][] paraMatrix) {
        weightMatrix = new IntMatrix(paraMatrix);
        numNodes = weightMatrix.getRows();
    }// Of the second constructor

    /**
     * ********************
     * Overrides the method claimed in Object, the superclass of any class.
     * ********************
     */
    public String toString() {
        String resultString = "This is the weight matrix of the graph.\r\n" + weightMatrix;
        return resultString;
    }// Of toString

    /**
     * ********************
     * The Dijkstra algorithm: shortest path from the source to all nodes.
     *
     * @param paraSource The source node.
     * @return The distances to all nodes.
     * ********************
     */
    public int[] dijkstra(int paraSource) {
        // Step 1. Initialize.
        int[] tempDistanceArray = new int[numNodes];
        for (int i = 0; i < numNodes; i++) {
            tempDistanceArray[i] = weightMatrix.getValue(paraSource, i);
        } // Of for i

        int[] tempParentArray = new int[numNodes];
        Arrays.fill(tempParentArray, paraSource);
        // -1 for no parent.
        tempParentArray[paraSource] = -1;

        // Visited nodes will not be considered further.
        boolean[] tempVisitedArray = new boolean[numNodes];
        tempVisitedArray[paraSource] = true;

        // Step 2. Main loops.
        int tempMinDistance;
        int tempBestNode = -1;
        for (int i = 0; i < numNodes - 1; i++) {
            // Step 2.1 Find out the best next node.
            tempMinDistance = Integer.MAX_VALUE;
            for (int j = 0; j < numNodes; j++) {
                // This node is visited.
                if (tempVisitedArray[j]) {
                    continue;
                } // Of if

                if (tempMinDistance > tempDistanceArray[j]) {
                    tempMinDistance = tempDistanceArray[j];
                    tempBestNode = j;
                } // Of if
            } // Of for j

            tempVisitedArray[tempBestNode] = true;

            // Step 2.2 Prepare for the next round.
            for (int j = 0; j < numNodes; j++) {
                // This node is visited.
                if (tempVisitedArray[j]) {
                    continue;
                } // Of if

                // This node cannot be reached.
                if (weightMatrix.getValue(tempBestNode, j) >= MAX_DISTANCE) {
                    continue;
                } // Of if

                if (tempDistanceArray[j] > tempDistanceArray[tempBestNode]
                        + weightMatrix.getValue(tempBestNode, j)) {
                    // Change the distance.
                    tempDistanceArray[j] = tempDistanceArray[tempBestNode]
                            + weightMatrix.getValue(tempBestNode, j);
                    // Change the parent.
                    tempParentArray[j] = tempBestNode;
                } // Of if
            } // Of for j

            // For test
            System.out.println("The distance to each node: " + Arrays.toString(tempDistanceArray));
            System.out.println("The parent of each node: " + Arrays.toString(tempParentArray));
        } // Of for i

        // Step 3. Output for debug.
        System.out.println("Finally");
        System.out.println("The distance to each node: " + Arrays.toString(tempDistanceArray));
        System.out.println("The parent of each node: " + Arrays.toString(tempParentArray));
        return tempDistanceArray;
    }// Of dijkstra

    /**
     * ********************
     * The minimal spanning tree.
     *
     * @return The total cost of the tree.
     * ********************
     */
    public int prim() {
        // Step 1. Initialize.
        // Any node can be the source.
        int tempSource = 0;
        int[] tempDistanceArray = new int[numNodes];
        for (int i = 0; i < numNodes; i++) {
            tempDistanceArray[i] = weightMatrix.getValue(tempSource, i);
        } // Of for i

        int[] tempParentArray = new int[numNodes];
        Arrays.fill(tempParentArray, tempSource);
        // -1 for no parent.
        tempParentArray[tempSource] = -1;

        // Visited nodes will not be considered further.
        boolean[] tempVisitedArray = new boolean[numNodes];
        tempVisitedArray[tempSource] = true;

        // Step 2. Main loops.
        int tempMinDistance;
        int tempBestNode = -1;
        for (int i = 0; i < numNodes - 1; i++) {
            // Step 2.1 Find out the best next node.
            tempMinDistance = Integer.MAX_VALUE;
            for (int j = 0; j < numNodes; j++) {
                // This node is visited.
                if (tempVisitedArray[j]) {
                    continue;
                } // Of if

                if (tempMinDistance > tempDistanceArray[j]) {
                    tempMinDistance = tempDistanceArray[j];
                    tempBestNode = j;
                } // Of if
            } // Of for j

            tempVisitedArray[tempBestNode] = true;

            // Step 2.2 Prepare for the next round.
            for (int j = 0; j < numNodes; j++) {
                // This node is visited.
                if (tempVisitedArray[j]) {
                    continue;
                } // Of if

                // This node cannot be reached.
                if (weightMatrix.getValue(tempBestNode, j) >= MAX_DISTANCE) {
                    continue;
                } // Of if

                // Attention: the difference from the Dijkstra algorithm.
                if (tempDistanceArray[j] > weightMatrix.getValue(tempBestNode, j)) {
                    // Change the distance.
                    tempDistanceArray[j] = weightMatrix.getValue(tempBestNode, j);
                    // Change the parent.
                    tempParentArray[j] = tempBestNode;
                } // Of if
            } // Of for j

            // For test
            System.out.println(
                    "The selected distance for each node: " + Arrays.toString(tempDistanceArray));
            System.out.println("The parent of each node: " + Arrays.toString(tempParentArray));
        } // Of for i

        int resultCost = 0;
        for (int i = 0; i < numNodes; i++) {
            resultCost += tempDistanceArray[i];
        } // Of for i

        // Step 3. Output for debug.
        System.out.println("Finally");
        System.out.println("The parent of each node: " + Arrays.toString(tempParentArray));
        System.out.println("The total cost: " + resultCost);

        return resultCost;
    }// Of prim

    /**
     *********************
     * Critical path. Net validity checks such as loop check not implemented.
     * The source should be 0 and the destination should be n-1.
     *
     * @return The node sequence of the path.
     *********************
     */
    public boolean[] criticalPath() {
        // One more value to save simple computation.
        int tempValue;

        // Step 1. The in-degree of each node.
        int[] tempInDegrees = new int[numNodes];
        for (int i = 0; i < numNodes; i++) {
            for (int j = 0; j < numNodes; j++) {
                if (weightMatrix.getValue(i, j) != -1) {
                    tempInDegrees[j]++;
                } // Of if
            } // Of for j
        } // Of for i
        System.out.println("In-degree of nodes: " + Arrays.toString(tempInDegrees));

        // Step 2. Topology sorting.
        int[] tempEarliestTimeArray = new int[numNodes];
        for (int i = 0; i < numNodes; i++) {
            // This node cannot be removed.
            if (tempInDegrees[i] > 0) {
                continue;
            } // Of if

            System.out.println("Removing " + i);

            for (int j = 0; j < numNodes; j++) {
                if (weightMatrix.getValue(i, j) != -1) {
                    tempValue = tempEarliestTimeArray[i] + weightMatrix.getValue(i, j);
                    if (tempEarliestTimeArray[j] < tempValue) {
                        tempEarliestTimeArray[j] = tempValue;
                    } // Of if
                    tempInDegrees[j]--;
                } // Of if
            } // Of for j
        } // Of for i

        System.out.println("Earlest start time: " + Arrays.toString(tempEarliestTimeArray));

        // Step 3. The out-degree of each node.
        int[] tempOutDegrees = new int[numNodes];
        for (int i = 0; i < numNodes; i++) {
            for (int j = 0; j < numNodes; j++) {
                if (weightMatrix.getValue(i, j) != -1) {
                    tempOutDegrees[i]++;
                } // Of if
            } // Of for j
        } // Of for i
        System.out.println("Out-degree of nodes: " + Arrays.toString(tempOutDegrees));

        // Step 4. Reverse topology sorting.
        int[] tempLatestTimeArray = new int[numNodes];
        for (int i = 0; i < numNodes; i++) {
            tempLatestTimeArray[i] = tempEarliestTimeArray[numNodes - 1];
        } // Of for i

        for (int i = numNodes - 1; i >= 0; i--) {
            // This node cannot be removed.
            if (tempOutDegrees[i] > 0) {
                continue;
            } // Of if

            System.out.println("Removing " + i);

            for (int j = 0; j < numNodes; j++) {
                if (weightMatrix.getValue(j, i) != -1) {
                    tempValue = tempLatestTimeArray[i] - weightMatrix.getValue(j, i);
                    if (tempLatestTimeArray[j] > tempValue) {
                        tempLatestTimeArray[j] = tempValue;
                    } // Of if
                    tempOutDegrees[j]--;
                    System.out.println("The out-degree of " + j + " decreases by 1.");
                } // Of if
            } // Of for j
        } // Of for i

        System.out.println("Latest start time: " + Arrays.toString(tempLatestTimeArray));

        boolean[] resultCriticalArray = new boolean[numNodes];
        for (int i = 0; i < numNodes; i++) {
            if (tempEarliestTimeArray[i] == tempLatestTimeArray[i]) {
                resultCriticalArray[i] = true;
            } // Of if
        } // Of for i

        System.out.println("Critical array: " + Arrays.toString(resultCriticalArray));
        System.out.print("Critical nodes: ");
        for (int i = 0; i < numNodes; i++) {
            if (resultCriticalArray[i]) {
                System.out.print(" " + i);
            } // Of if
        } // Of for i
        System.out.println();

        return resultCriticalArray;
    }// Of criticalPath

}// Of class Net

五. 数据测试

此次代码内部数据对应的AOE图如图H1所示，对应的邻接矩阵如图H2所示

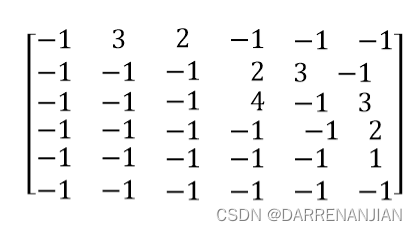
代码运行的结果（部分）：

六. 总结与反思

关键路径的代码难以理解的地方很多，这个需要我们把握名词的每一个定义，类似于什么是AOV网，AOE网？它们的区别是什么？什么是拓补排序？拓扑排序和关键路径的联系在哪里等等之类。除此之外我们还需要理解算法的逻辑思维过程，只有把握好这两个方面才有可能看的懂闵老师写的代码（这里不得不说闵老师的代码写的真的很清楚，我感觉理解的很快QAQ）。上述完成之后，意指算法部分完成，代码的话就是要根据算法的思维过程逢山开路，遇水架桥（像这一小节里面的出度，入度这里算法和代码其实是有一个转化过程的）需要什么补充什么，最后对于代码里面实在理解不到的地方，我的建议是用人脑模拟计算机运行一遍（这招非常有用，有时候我不知道这个变量是干什么的，当我自己模拟运行一次之后豁然开朗）。

最后补充一句吧：路漫漫其修远兮，吾将上下而求索，加油吧少年！！！