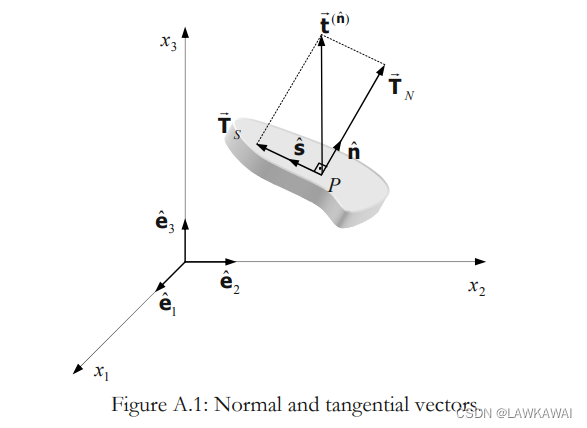
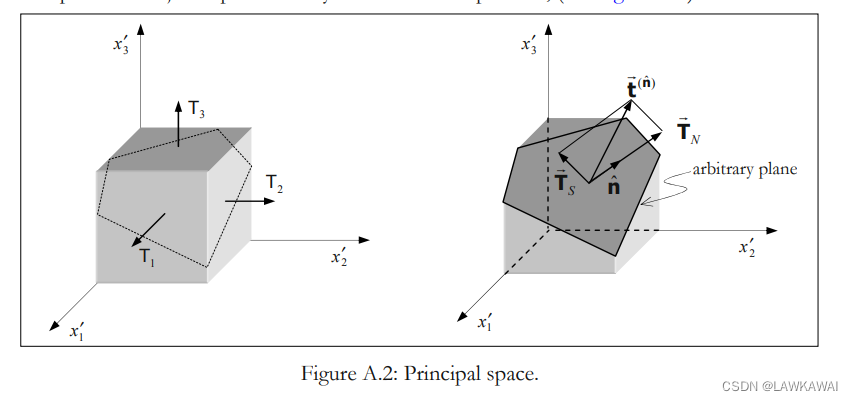
二阶张量在特定方向的投影
法向和切向分量
二阶张量T投影到
n
^
\hat n
n^方向的结果是
t
⃗
(
n
^
)
=
T
⋅
n
^
\vec t^{(\hat n)}=T \cdot \hat n
t(n^)=T⋅n^,其中
t
⃗
(
n
^
)
\vec t^{(\hat n)}
t(n^)可以分解成:
t
⃗
(
n
^
)
=
T
⃗
N
+
T
⃗
S
\vec t^{(\hat n)}=\vec T_N+\vec T_S
t(n^)=TN+TS
其中,
T
⃗
N
\vec T_N
TN是法向量,
T
⃗
S
\vec T_S
TS是切向量
如果记
n
^
\hat n
n^和
s
^
\hat s
s^是
T
⃗
N
\vec T_N
TN和
T
⃗
S
\vec T_S
TS方向的单位向量,那么可以表示成:
t
⃗
(
n
^
)
=
T
N
n
^
+
T
S
s
^
\vec t^{(\hat n)}=T_N\hat n+T_S\hat s
t(n^)=TNn^+TSs^
其中,
T
N
T_N
TN和
T
S
T_S
TS是
T
⃗
N
\vec T_N
TN和
T
⃗
S
\vec T_S
TS的大小
向量
T
⃗
N
\vec T_N
TN如下所示:
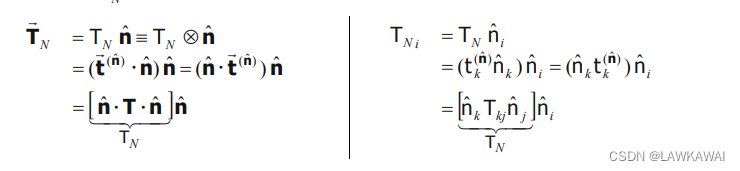
因此:
T
N
=
t
⃗
(
n
^
)
⋅
n
^
=
n
^
⋅
T
⋅
n
^
=
n
^
k
T
k
j
n
^
j
T_N = \vec t^{(\hat n)}\cdot \hat n=\hat n \cdot T \cdot \hat n=\hat n_kT_{kj}\hat n_j
TN=t(n^)⋅n^=n^⋅T⋅n^=n^kTkjn^j
之前有讨论过,若对于所有的 n ^ ≠ 0 \hat n \neq 0 n^=0,有 T N = n ^ ⋅ T ⋅ n ^ > 0 T_N=\hat n \cdot T\cdot \hat n>0 TN=n^⋅T⋅n^>0,则 T T T是正定张量,并且可以表示成: T N = n ^ ⋅ T ⋅ n ^ = n ^ ⋅ T s y m ⋅ n ^ T_N = \hat n \cdot T \cdot \hat n=\hat n \cdot T^{sym} \cdot \hat n TN=n^⋅T⋅n^=n^⋅Tsym⋅n^
所以,如果一个张量的对称部分是正定的,那么这个张量也是正定的
向量
T
⃗
S
\vec T_S
TS可以表示成:
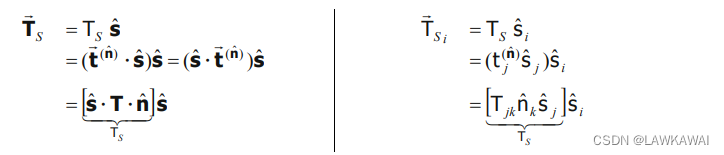
也可以表示成如下所示:
T
⃗
S
=
t
⃗
(
n
^
)
−
T
⃗
N
=
T
⋅
n
^
−
[
T
:
(
n
^
⨂
n
^
)
]
n
^
\vec T_S = \vec t^{(\hat n)}-\vec T_N=T\cdot \hat n-[T:(\hat n \bigotimes \hat n)]\hat n
TS=t(n^)−TN=T⋅n^−[T:(n^⨂n^)]n^
T
⃗
S
\vec T_S
TS的大小可以由勾股定理得到:
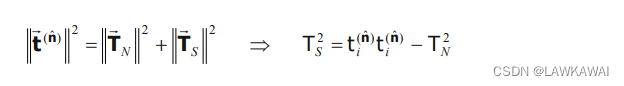
其中:
t
i
(
n
^
)
t
i
(
n
^
)
=
T
i
j
T
i
k
n
j
n
k
t_i^{(\hat n)}t_i^{(\hat n)}=T_{ij}T_{ik}n_jn_k
ti(n^)ti(n^)=TijTiknjnk
思考:在哪个平面才是最大的法向和切向分量?
问题A.1 证明 T ⃗ S = t ⃗ ( n ^ ) ⋅ ( 1 − n ^ ⨂ n ^ ) \vec T_S = \vec t^{(\hat n)}\cdot (1-\hat n\bigotimes \hat n) TS=t(n^)⋅(1−n^⨂n^),其中 t ⃗ ( n ^ ) \vec t ^{(\hat n)} t(n^)就是二阶张量 T T T投影到方向 n ^ \hat n n^的结果, T ⃗ S \vec T_S TS是切向向量

法向分量的最大和最小值
法向分量为
T
N
=
n
^
⋅
T
⋅
n
^
T_N = \hat n\cdot T \cdot \hat n
TN=n^⋅T⋅n^,满足
n
^
⋅
n
^
=
1
\hat n \cdot \hat n = 1
n^⋅n^=1约束条件。那么求在这个约束条件下
T
N
T_N
TN的最大最小值可以使用拉格朗日乘子法:
L
(
n
^
,
μ
)
=
T
N
−
μ
(
n
^
⋅
n
^
−
1
)
=
n
^
⋅
T
⋅
n
^
−
μ
(
n
^
⋅
n
^
−
1
)
\mathcal{L}(\hat n, \mu)=T_N-\mu (\hat n \cdot \hat n-1)=\hat n\cdot T \cdot \hat n-\mu (\hat n \cdot \hat n-1)
L(n^,μ)=TN−μ(n^⋅n^−1)=n^⋅T⋅n^−μ(n^⋅n^−1)
其中,
μ
\mu
μ是拉格朗日乘子,那么函数
L
\mathcal{L}
L关于
μ
\mu
μ和
n
^
\hat n
n^的导数为:
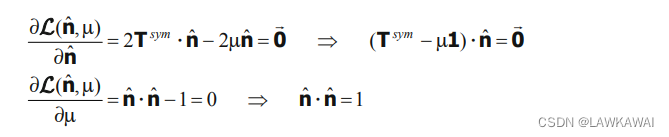
第一行有解当且仅当
det
(
T
s
y
m
−
1
)
=
0
\det(T^{sym}-1)=0
det(Tsym−1)=0,这是关于张量T的对称部分的特征值问题。
也就是说, T N T_N TN的最大最小值问题跟 T s y m T^{sym} Tsym的特征值相关。
现在,假设有
T
1
s
y
m
,
T
2
s
y
m
,
T
3
s
y
m
T_1^{sym}, T_2^{sym}, T_3^{sym}
T1sym,T2sym,T3sym作为
T
s
y
m
T^{sym}
Tsym的特征值,那么可以重组这些值为:
T
I
s
y
m
>
T
I
I
s
y
m
>
T
I
I
I
s
y
m
T_I^{sym}>T_{II}^{sym}>T_{III}^{sym}
TIsym>TIIsym>TIIIsym
那么,
T
N
T_N
TN的最大值记为
T
I
s
y
m
T_I^{sym}
TIsym, 最小值记为
T
I
I
I
s
y
m
T_{III}^{sym}
TIIIsym
NOTE: 反对称部分在法向量中不起作用,因为 T N = n ^ ⋅ T ⋅ n ^ = n ^ ⋅ T s y m ⋅ n ^ T_N = \hat n \cdot T \cdot \hat n = \hat n \cdot T^{sym} \cdot \hat n TN=n^⋅T⋅n^=n^⋅Tsym⋅n^
切向分量的最大最小值
为了方便,将在T的主空间讨论,分量表示为法向分量
那么,方向
n
^
\hat n
n^的法向分量
T
N
T_N
TN,如下所示:
T
N
=
t
i
(
n
^
)
n
^
i
=
T
i
j
n
^
i
n
^
j
=
T
1
n
^
1
2
+
T
2
n
^
2
2
+
T
3
n
^
3
2
T_N=t_i^{(\hat n)}\hat n_i=T_{ij}\hat n_i\hat n_j=T_1\hat n_1^2+T_2\hat n_2^2+T_3\hat n_3^2
TN=ti(n^)n^i=Tijn^in^j=T1n^12+T2n^22+T3n^32
在特定的方向 n ^ i = [ 1 , 0 , 0 ] ⟹ T N = T i \hat n _i= [1, 0, 0] \implies T_N=T_i n^i=[1,0,0]⟹TN=Ti
切向分量如下所示:
T
S
2
=
∣
∣
t
⃗
(
n
^
)
∣
∣
2
−
T
N
2
=
t
i
(
n
^
)
t
i
(
n
^
)
−
T
N
2
=
T
i
j
T
i
k
n
^
j
n
^
k
−
T
N
2
T_S^2=||\vec t^{(\hat n)}||^2-T_N^2=t_i^{(\hat n)}t_i^{(\hat n)}-T_N^2=T_{ij}T_{ik}\hat n_j\hat n_k-T_N^2
TS2=∣∣t(n^)∣∣2−TN2=ti(n^)ti(n^)−TN2=TijTikn^jn^k−TN2
代入
T
N
=
t
i
(
n
^
)
n
^
i
=
T
i
j
n
^
i
n
^
j
T_N=t_i^{(\hat n)}\hat n_i=T_{ij}\hat n_i\hat n_j
TN=ti(n^)n^i=Tijn^in^j,有:
T
S
2
=
T
1
2
n
1
2
+
T
2
2
n
2
2
+
T
3
2
n
3
2
−
(
T
1
n
^
1
2
+
T
2
n
^
2
2
+
T
3
n
^
3
2
)
2
T_S^2=T_1^2n_1^2+T_2^2n_2^2+T_3^2n_3^2-(T_1\hat n_1^2+T_2\hat n_2^2+T_3\hat n_3^2)^2
TS2=T12n12+T22n22+T32n32−(T1n^12+T2n^22+T3n^32)2
现在如果问:
n
^
i
\hat n_i
n^i取什么值才能使得函数
T
S
2
T_S^2
TS2等于最大最小值,这个问题等价于:
F
(
n
^
)
=
T
S
2
−
μ
(
n
^
i
n
^
i
−
1
)
F(\hat n)=T_S^2-\mu(\hat n_i\hat n_i-1)
F(n^)=TS2−μ(n^in^i−1)
其中,
μ
\mu
μ是拉格朗日乘子,约束条件为
n
^
⋅
n
^
=
1
\hat n \cdot \hat n = 1
n^⋅n^=1,那么:
∂
F
(
n
^
)
∂
n
j
=
0
j
;
∂
F
(
n
^
)
∂
μ
=
0
\frac{\partial F(\hat n)}{\partial n_j}=0_j; \quad \frac{\partial F(\hat n)}{\partial \mu}=0
∂nj∂F(n^)=0j;∂μ∂F(n^)=0
解以上方程组,得到:
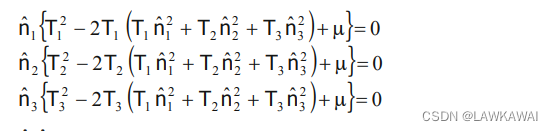
那么,可能的解如下所示:

前三组解:提供了 T S T_S TS的最小值,为0,正好对应于主方向
(4), (5), (6)这三组解,所表示的平面如下图所示:
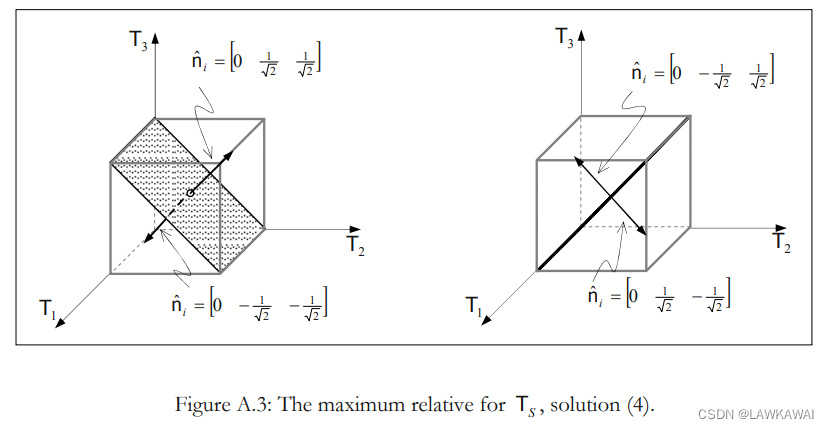
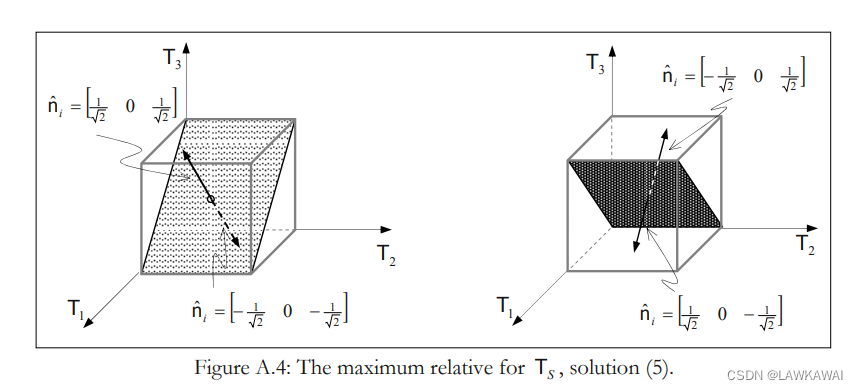
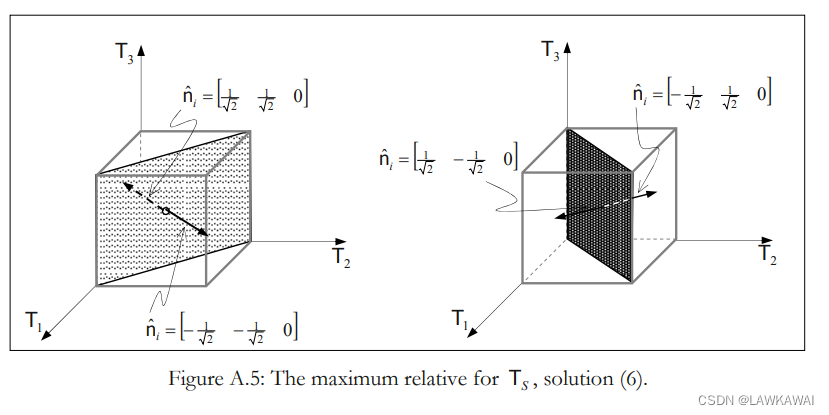
对
T
1
,
T
2
,
T
3
T_1, T_2, T_3
T1,T2,T3进行排序,那么,
T
S
T_S
TS可以表示成
T
I
,
T
I
I
,
T
I
I
I
T_I, T_{II}, T_{III}
TI,TII,TIII的形式:
T
S
m
a
x
=
T
I
−
T
I
I
I
2
T_{Smax}=\frac{T_I-T_{III}}{2}
TSmax=2TI−TIII
任意二阶张量的图像表示
如果给定一个二阶张量的笛卡尔分量,那么就可以列出在任意由法向量 n ^ \hat n n^ 定义的平面上的法向和切向分量 ( T N , T S ) (T_N, T_S) (TN,TS)
约束条件是: n ^ ⋅ n ^ = n ^ 1 2 + n ^ 2 2 + n ^ 3 2 = 1 \hat n \cdot \hat n = \hat n_1^2+\hat n_2^2+\hat n_3^2=1 n^⋅n^=n^12+n^22+n^32=1
可以画出以 T N T_N TN为横坐标, T S T_S TS为纵坐标的图像
数值过程:
先随机列举几个不同的
n
^
\hat n
n^,这样就可以得到不同的
(
T
N
,
T
S
)
(T_N, T_S)
(TN,TS),把点画在
T
N
×
T
S
T_N \times T_S
TN×TS的图像中
同样,可以建立一个由其对称部分构成的图像: T N s y m × T S s y m T_N^{sym} \times T_S^{sym} TNsym×TSsym
第一个例子:对称的正定张量, T N = n ^ ⋅ T ⋅ n ^ > 0 , f o r a l l n ^ ≠ 0 ⃗ T_N = \hat n \cdot T \cdot \hat n>0, \quad for \quad all \quad \hat n \neq \vec 0 TN=n^⋅T⋅n^>0,foralln^=0
可以证明,有三个特征值对应的是 T S = 0 T_S = 0 TS=0
由下图可以看出,
T
N
T_N
TN的最大最小值对其对称部分的最大最小值

对于切向向量,可以得到以下分解:
T
⃗
S
=
[
s
^
⋅
T
⋅
n
^
]
s
^
=
[
s
^
⋅
T
s
y
m
⋅
n
^
+
s
^
⋅
T
s
k
e
w
⋅
n
^
]
s
^
\vec T_S = [\hat s \cdot T \cdot \hat n]\hat s=[\hat s \cdot T^{sym}\cdot \hat n+\hat s \cdot T^{skew}\cdot \hat n]\hat s
TS=[s^⋅T⋅n^]s^=[s^⋅Tsym⋅n^+s^⋅Tskew⋅n^]s^
当
n
^
\hat n
n^ 是对称部分的其中的一个主方向时,有:

其中
s
^
⋅
n
^
=
0
\hat s \cdot \hat n = 0
s^⋅n^=0,因为单位向量
s
^
\hat s
s^和
n
^
\hat n
n^是正交的
所以,切向分量如下所示:
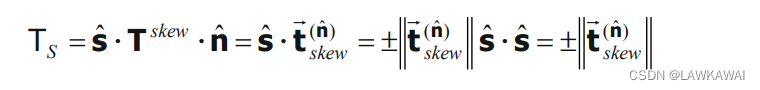
以上公式仅适用于
n
^
\hat n
n^是
T
s
y
m
T^{sym}
Tsym主方向的其中一个
对于特征值
T
I
s
y
m
=
10.55
T_I^{sym}=10.55
TIsym=10.55,对应的特征向量
n
^
j
(
1
)
=
[
−
0.4522937
;
−
0.561517458
;
0.692913086
]
\hat n_j^{(1)}=[-0.4522937; -0.561517458; 0.692913086]
n^j(1)=[−0.4522937;−0.561517458;0.692913086],有:

而对于特征值
T
I
I
s
y
m
=
3.61
T_{II}^{sym}=3.61
TIIsym=3.61, 有:
s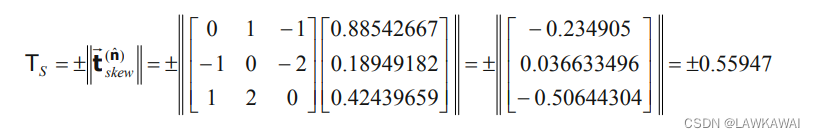
对于特征值
T
I
I
I
s
y
m
=
0.84
T_{III}^{sym}=0.84
TIIIsym=0.84, 有:

可以发现,T的最大和最小的法向分量对应的是
T
s
y
m
T^{sym}
Tsym的特征值,
例如, T N m a x = T I s y m = 10.55 T_{N_{max}}=T_I^{sym}=10.55 TNmax=TIsym=10.55, T N m i n = T I I I s y m = 0.84 T_{N_{min}}=T_{III}^{sym}=0.84 TNmin=TIIIsym=0.84
那么最大的切向分量等于圆的半径,即由
T
I
s
y
m
=
10.55
T_I^{sym}=10.55
TIsym=10.55 和
T
I
I
I
s
y
m
=
0.84
T_{III}^{sym}=0.84
TIIIsym=0.84构成的:
T
S
m
a
x
s
y
m
=
10.55
−
0.84
2
=
4.86
T_{S_{max}}^{sym}=\frac{10.55-0.84}{2}=4.86
TSmaxsym=210.55−0.84=4.86
第二个例子:
对称张量有两个相同的特征值,可以验证 ( T N , T S ) (T_N, T_S) (TN,TS)可取的值被限制在以半径 R = T I − T I I I 2 = 2.5 R = \frac{T_I-T_{III}}{2}=2.5 R=2TI−TIII=2.5, 以及圆中心为 ( T N = T I + T I I I 2 = 1.5 , T S = 0 ) (T_N=\frac{T_I+T_{III}}{2}=1.5, T_S=0) (TN=2TI+TIII=1.5,TS=0)上的圆
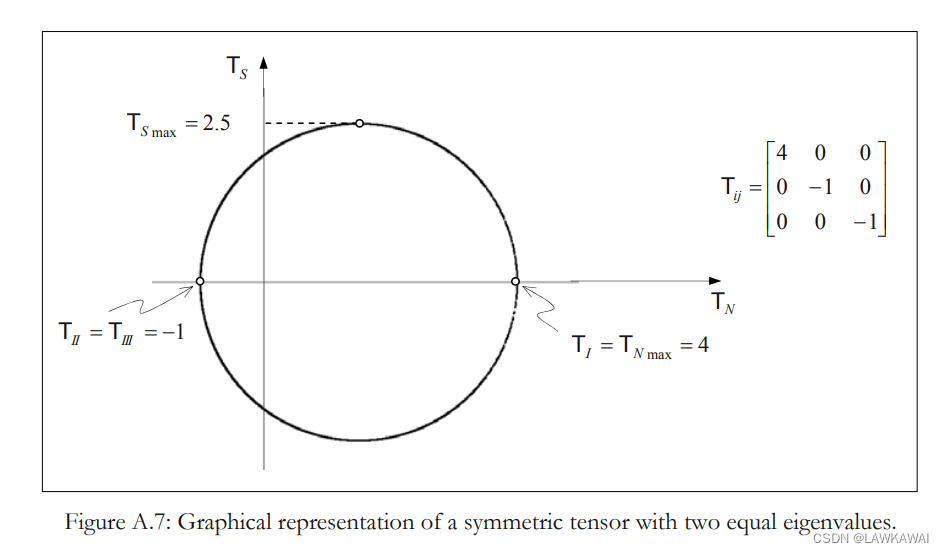
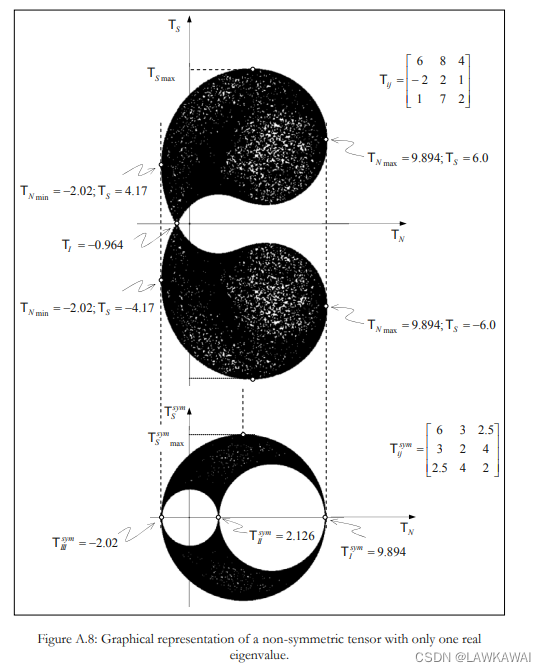
第三个例子:非对称张量
只有一个实数特征值,为 T I = − 0.964 T_I= -0.964 TI=−0.964
在T的对称部分的主方向上,可以列出切向分量的值:
对于特征值
T
I
s
y
m
=
9.894
T_{I}^{sym}=9.894
TIsym=9.894,有:

对于特征值
T
I
I
I
s
y
m
=
−
2.02
T_{III}^{sym}=-2.02
TIIIsym=−2.02, 有:

对称二阶张量的图像表示(莫尔圆)
有:
T
S
2
+
T
N
2
=
t
⃗
(
n
^
)
⋅
t
⃗
(
n
^
)
=
∣
∣
t
⃗
(
n
^
)
∣
∣
2
T_S^2+T_N^2=\vec t^{(\hat n)}\cdot \vec t^{(\hat n)}=||\vec t ^{(\hat n)}||^2
TS2+TN2=t(n^)⋅t(n^)=∣∣t(n^)∣∣2
主空间的
t
⃗
(
n
^
)
=
T
⋅
n
^
\vec t^{(\hat n)}=T \cdot \hat n
t(n^)=T⋅n^的分量,由下给出:


那么点乘
t
⃗
(
n
^
)
⋅
t
⃗
(
n
^
)
\vec t^{(\hat n)} \cdot \vec t^{(\hat n)}
t(n^)⋅t(n^), 如下所示:
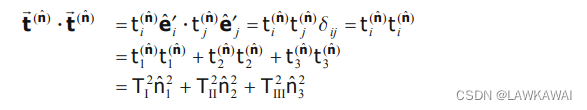
那么:
T
S
2
+
T
N
2
=
T
I
2
n
^
1
2
+
T
I
I
2
n
^
2
2
+
T
I
I
I
2
n
^
3
2
T_S^2+T_N^2 = T_I^2\hat n_1^2+T_{II}^2\hat n_2^2+T_{III}^2\hat n_3^2
TS2+TN2=TI2n^12+TII2n^22+TIII2n^32
那么,在主空间的法向分量
T
N
T_N
TN,可以写成:
T
N
=
t
⃗
(
n
^
)
⋅
T
=
T
i
j
n
^
i
n
^
j
=
T
I
n
^
1
2
+
T
I
I
n
^
2
2
+
T
I
I
I
n
^
1
2
T_N = \vec t ^{(\hat n)} \cdot T=T_{ij}\hat n_i\hat n_j=T_I\hat n_1^2+T_{II}\hat n_2^2+T_{III}\hat n_1^2
TN=t(n^)⋅T=Tijn^in^j=TIn^12+TIIn^22+TIIIn^12
考虑约束条件:
n
^
i
n
^
i
=
1
⟹
n
^
1
2
=
1
−
n
^
2
2
−
n
^
3
2
\hat n_i \hat n_i=1 \implies \hat n_1^2 = 1-\hat n_2^2-\hat n_3^2
n^in^i=1⟹n^12=1−n^22−n^32, 代入到上式,求出
n
^
2
2
\hat n_2^2
n^22:
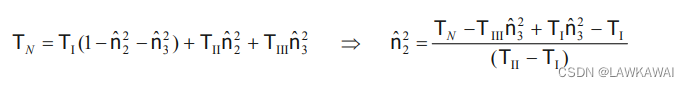
n
^
1
2
=
1
−
n
^
2
2
−
n
^
3
2
\hat n_1^2 = 1-\hat n_2^2-\hat n_3^2
n^12=1−n^22−n^32代入公式:
T
S
2
+
T
N
2
=
T
I
2
n
^
1
2
+
T
I
I
2
n
^
2
2
+
T
I
I
I
2
n
^
3
2
T_S^2+T_N^2 = T_I^2\hat n_1^2+T_{II}^2\hat n_2^2+T_{III}^2\hat n_3^2
TS2+TN2=TI2n^12+TII2n^22+TIII2n^32
可得:

再代入
n
^
2
2
\hat n_2^2
n^22,得:
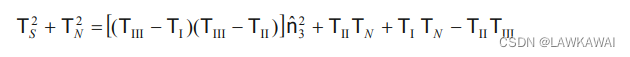
得到
n
^
3
2
\hat n_3^2
n^32:
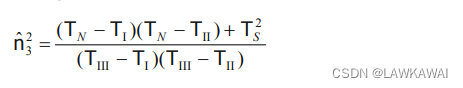
所以,也可以用相似得方式求出
n
^
1
2
\hat n_1^2
n^12 和
n
^
2
2
\hat n_2^2
n^22, 如下所示:

若
T
I
>
T
I
I
>
T
I
I
I
T_I > T_{II} > T_{III}
TI>TII>TIII, (a)和©的分母都为正,那么分子也为正;(b)分母为负,那么分子也必须为负
例如:
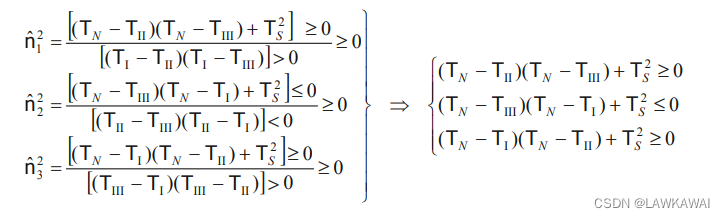
经过代数变换:
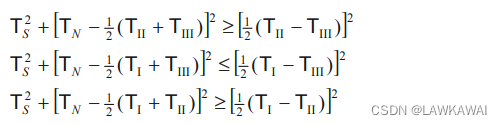
以上的等式表示是圆
第一个圆
中心:
(
1
2
(
T
I
I
+
T
I
I
I
)
,
0
)
(\frac{1}{2}(T_{II}+T_{III}), 0)
(21(TII+TIII),0)
半径:
1
2
(
T
I
I
−
T
I
I
I
)
\frac{1}{2}(T_{II}-T_{III})
21(TII−TIII)
第一个可行域是在圆
C
1
C_1
C1之外:
第二个圆
中心:
(
1
2
(
T
I
+
T
I
I
I
)
,
0
)
(\frac{1}{2}(T_{I}+T_{III}), 0)
(21(TI+TIII),0)
半径:
1
2
(
T
I
−
T
I
I
I
)
\frac{1}{2}(T_{I}-T_{III})
21(TI−TIII)
第二个可行域是在圆
C
2
C_2
C2之内:
第三个圆
中心:
(
1
2
(
T
I
+
T
I
I
)
,
0
)
(\frac{1}{2}(T_{I}+T_{II}), 0)
(21(TI+TII),0)
半径:
1
2
(
T
I
−
T
I
I
)
\frac{1}{2}(T_{I}-T_{II})
21(TI−TII)
第三个可行域是在圆
C
3
C_3
C3之外:
所以,可行域如下所示:
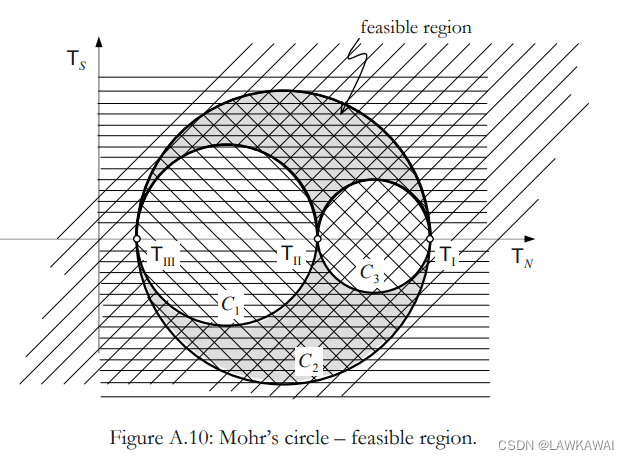
在莫尔圆中,最大值
T
S
m
a
x
T_{S_{max}}
TSmax的解:
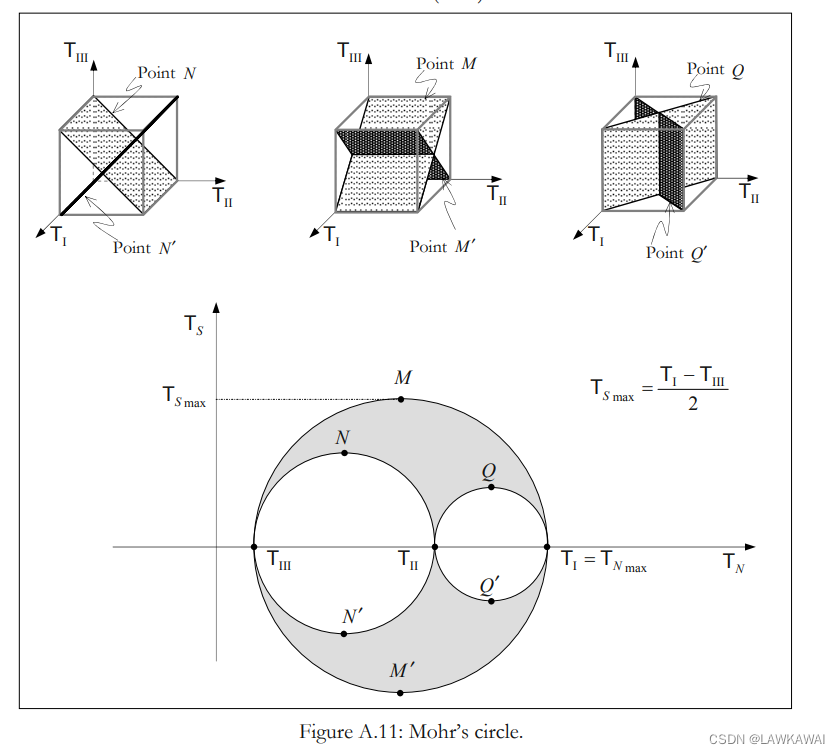
张量椭球
对称二阶张量T在主空间的特征值
(
T
1
,
T
2
,
T
3
)
(T_1, T_2, T_3)
(T1,T2,T3) , 满足以下:

现在,在主空间定义一个曲面,这个曲面可以描述
n
^
\hat n
n^ 的所有可能值得向量
t
⃗
(
n
^
)
\vec t ^{(\hat n)}
t(n^)
由约束条件:
n
^
1
2
+
n
^
2
2
+
n
^
3
2
=
1
\hat n_1^2+ \hat n_2^2+\hat n_3^2=1
n^12+n^22+n^32=1, 有:
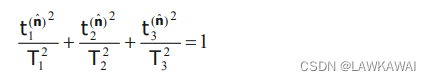
这个表示得是一个在T主空间得椭球。如下所示
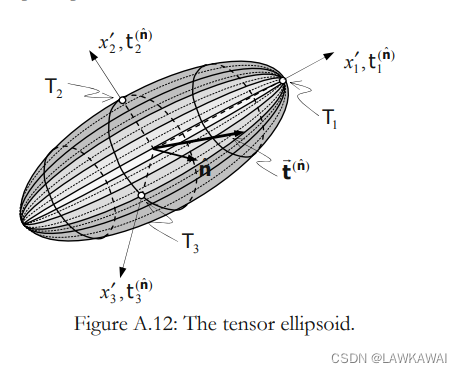
椭球表面表示的是
t
1
,
t
2
,
t
3
t_1, t_2, t_3
t1,t2,t3的可能取值
当两个特征值相等,那么就会得到一个旋转的椭球
当三个特征值相等,那么得到一个球, 此时表现出这种性质的张量被称为球面张量,任意方向都是主方向
球面张量和偏张量的图像表示
八面体向量
八面体平面,又称作偏平面,在这个平面上的法向与主方向的夹角都相等
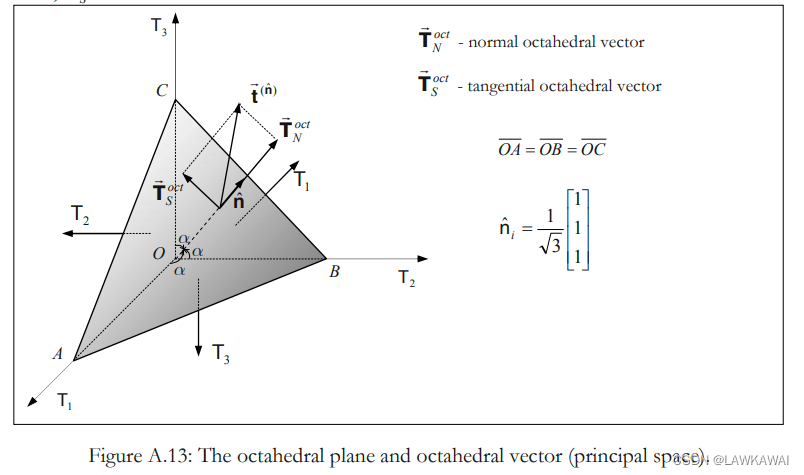
n
^
1
=
n
^
2
=
n
^
3
\hat n_1=\hat n_2 = \hat n_3
n^1=n^2=n^3, 有:
3
n
^
1
2
=
1
3\hat n_1^2=1
3n^12=1 , 所以:
n
^
i
=
[
1
3
1
3
1
3
]
\hat n_i= [\frac{1}{\sqrt{3}} \quad \frac{1}{\sqrt{3}} \quad \frac{1}{\sqrt{3}}]
n^i=[313131]
二阶张量投影到一个八面体平面得到的向量,标记为八面体向量 t ⃗ ( n ^ ) \vec t ^{(\hat n)} t(n^), 可以分解为法向分量和切向分量,
定义法向八面体向量 T ⃗ N o c t \vec T_N^{oct} TNoct, 切向八面体向量 T ⃗ S o c t \vec T_S^{oct} TSoct
八面体向量可以表示成:
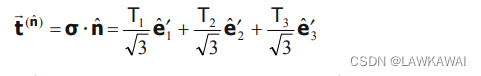
那么,
T
⃗
N
o
c
t
\vec T_N^{oct}
TNoct 的大小可以用
T
⃗
N
o
c
t
\vec T_N^{oct}
TNoct投影到
n
^
\hat n
n^来表示:
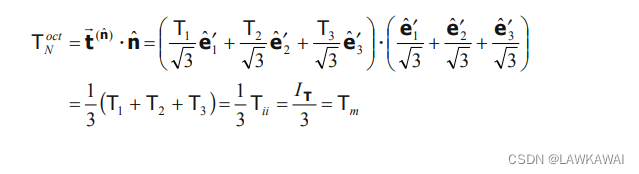
其中
T
N
o
c
t
T_N^{oct}
TNoct称为 八面体法向分量
那么,八面体切向分量
T
S
o
c
t
T_S^{oct}
TSoct,如下所示:
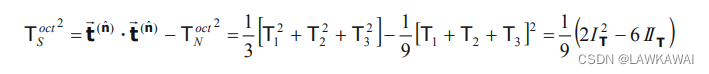
以上式子同样可以表示成:
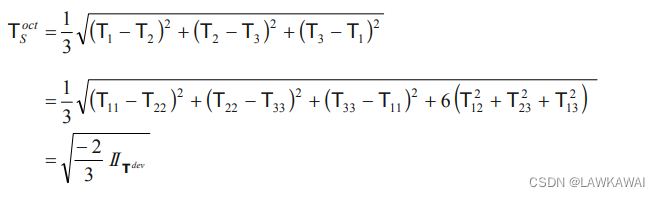
或者表示偏张量:
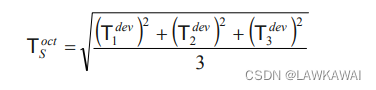
总结:

八面体法向和切向分量是8个八面体平面:
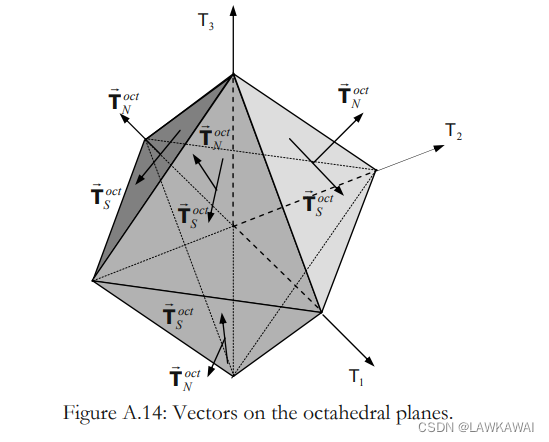
在主空间表示点
P
(
T
1
,
T
2
,
T
3
)
P(T_1, T_2, T_3)
P(T1,T2,T3),如下所示:

任意与直线 O A ‾ \overline{OA} OA 垂直的平面是八面体的(偏的),并且经过原点的八面体平面为 Π \Pi Π, 最后,直线 O A ‾ \overline{OA} OA 被称为球轴(净水轴)
考虑一个偏平面穿过点P,标记为 Π ′ \Pi' Π′, 定义三个向量 O P ⃗ , O A ⃗ , A P ⃗ \vec {OP}, \vec {OA}, \vec {AP} OP,OA,AP
O
P
⃗
\vec {OP}
OP 可以表示成T的主值:
O
P
⃗
=
T
1
e
^
1
′
+
T
2
e
^
2
′
+
T
3
e
^
3
′
\vec {OP} = T_1 \hat e_1'+T_2 \hat e_2'+T_3 \hat e_3'
OP=T1e^1′+T2e^2′+T3e^3′
根据上面的图像,
O
A
⃗
\vec {OA}
OA 的大小表示为:
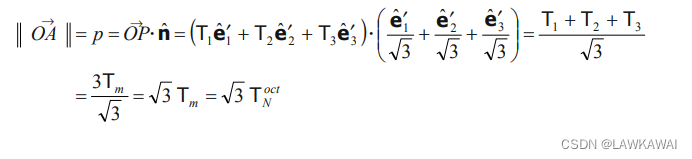
p = 3 T m = 3 T N o c t \boxed{p=\sqrt{3}T_m=\sqrt{3}T_N^{oct}} p=3Tm=3TNoct
因此,向量
O
A
⃗
\vec {OA}
OA 表示为:
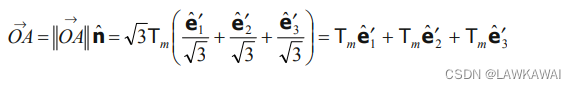
那么就可以求出
A
P
⃗
\vec {AP}
AP:
A
P
⃗
=
O
P
⃗
−
O
A
⃗
\vec {AP} = \vec {OP} - \vec {OA}
AP=OP−OA
由于:
O
P
⃗
=
T
1
e
^
1
′
+
T
2
e
^
2
′
+
T
3
e
^
3
′
\vec {OP} = T_1 \hat e_1'+T_2 \hat e_2'+T_3 \hat e_3'
OP=T1e^1′+T2e^2′+T3e^3′
所以,有:
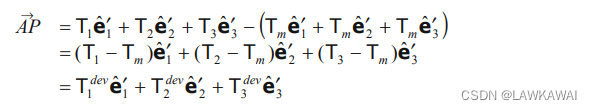
利用定义
T
i
j
d
e
v
=
T
i
j
−
T
m
δ
i
j
T_{ij}^{dev} = T_{ij}-T_m \delta_{ij}
Tijdev=Tij−Tmδij,有:
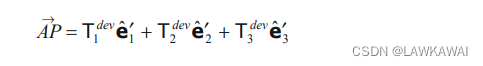
AP的分量表示的是主值的偏部分
T
i
j
d
e
v
T_{ij}^{dev}
Tijdev
A
P
⃗
\vec {AP}
AP的大小为:
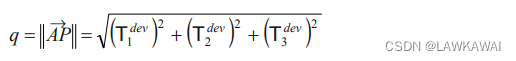
考虑
2
I
I
T
d
e
v
=
−
(
T
1
d
e
v
)
2
−
(
T
2
d
e
v
)
2
−
(
T
3
d
e
v
)
2
2II_{T^{dev}}=-(T_1^{dev})^2-(T_2^{dev})^2-(T_3^{dev})^2
2IITdev=−(T1dev)2−(T2dev)2−(T3dev)2
有:
q
=
−
2
I
I
T
d
e
v
=
3
T
S
o
c
t
\boxed{q = \sqrt{-2II_{T^{dev}}}=\sqrt{3}T_S^{oct}}
q=−2IITdev=3TSoct
根据毕达哥拉斯定理,也可以得到:
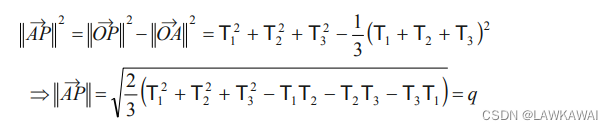
q: 表示张量状态距离球面状态的距离
考虑将主空间投影到
Π
\Pi
Π 平面
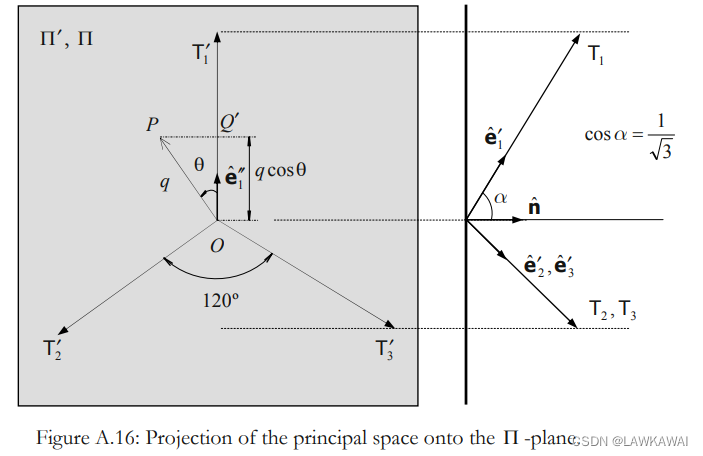
单位向量
e
^
1
′
′
=
a
1
e
^
1
′
+
a
2
e
^
2
′
+
a
3
e
^
3
′
\hat e_1''=a_1 \hat e_1'+a_2 \hat e_2'+a_3 \hat e_3'
e^1′′=a1e^1′+a2e^2′+a3e^3′
其中:
cos
β
=
sin
α
=
2
3
=
a
1
\cos \beta=\sin \alpha=\frac{\sqrt{2}}{\sqrt{3}}=a_1
cosβ=sinα=32=a1,
a
2
=
a
3
a_2 = a_3
a2=a3
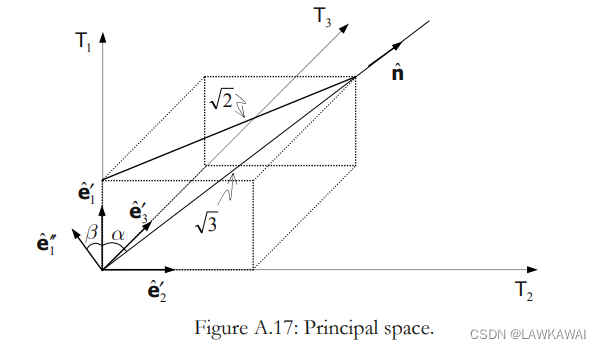
如果净水轴与偏平面是正交的,那么:
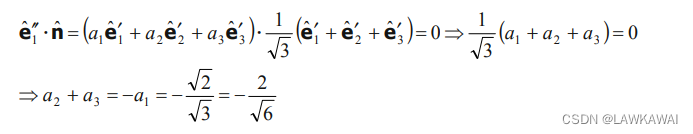
解得:

因此:
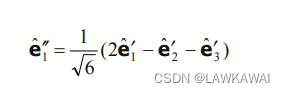
那么,
O
P
⃗
\vec {OP}
OP 在
e
^
1
′
′
\hat e_1''
e^1′′ 的投影如下所示:
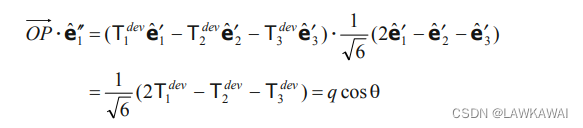
如果考虑
T
1
d
e
v
+
T
2
d
e
v
+
T
3
d
e
v
=
0
T_1^{dev}+T_2^{dev}+T_3^{dev}=0
T1dev+T2dev+T3dev=0 , 那么
−
T
1
d
e
v
=
T
2
d
e
v
+
T
3
d
e
v
-T_1^{dev}=T_2^{dev}+T_3^{dev}
−T1dev=T2dev+T3dev, 则上式变为:
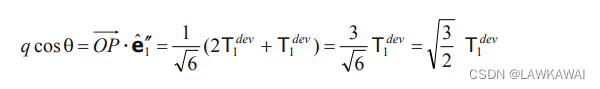
由于
q
=
−
2
I
I
T
d
e
v
q = \sqrt{-2II_{T^{dev}}}
q=−2IITdev, 有:

同样地,可以求出
T
2
d
e
v
T_2^{dev}
T2dev 和
T
3
d
e
v
T_3^{dev}
T3dev
那么,可以将主值表示为, T i j = T m δ i j + T i j d e v T_{ij}=T_m\delta_{ij}+T_{ij}^{dev} Tij=Tmδij+Tijdev

其中
0
≤
θ
≤
π
/
3
0 \le \theta \le \pi / 3
0≤θ≤π/3
所以,张量可以表示成 ( p , q , θ ) (p, q, \theta ) (p,q,θ)
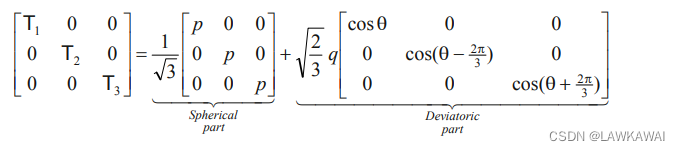
由于:

且有:
cos
3
θ
=
4
cos
3
θ
−
3
cos
θ
\cos 3\theta=4\cos^3 \theta -3\cos \theta
cos3θ=4cos3θ−3cosθ, 代入可得:
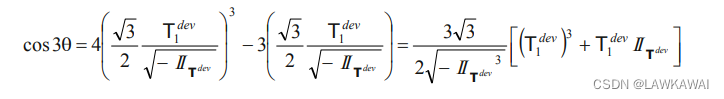
并且有:
I
I
T
d
e
v
=
(
T
1
d
e
v
T
2
d
e
v
+
T
2
d
e
v
T
3
d
e
v
+
T
1
d
e
v
T
3
d
e
v
)
II_{T^{dev}}=(T_1^{dev}T_2^{dev}+T_2^{dev}T_3^{dev}+T_1^{dev}T_3^{dev})
IITdev=(T1devT2dev+T2devT3dev+T1devT3dev)
那么:
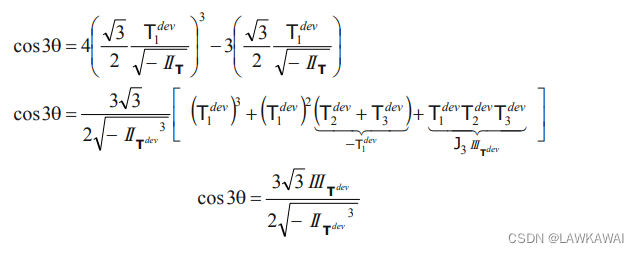
由于
I
I
T
d
e
v
II_{T^{dev}}
IITdev 和
I
I
I
T
d
e
v
III_{T^{dev}}
IIITdev是不变量,所以
cos
3
θ
\cos 3\theta
cos3θ也是不变量
参考教材:
Eduardo W.V. Chaves, Notes On Continuum Mechanics