求第n个斐波那契数列

斐波那契数 0 1 1 2 3 5 数列默认从0开始

	public static int fib1(int n) {
		if(n <= 1) return n;
		
		return fib1(n-1) + fib1(n-2);
	}
	
	public static int fib2(int n) {
		if(n <= 1) return n;
		
		int first = 0;
		int secend = 1;
		
		for (int i = 0; i < n-1; i++) {
			int sum = first + secend;
			first = secend;
			secend = sum;
		}
		
		return secend;
	}
	

如何评价一个算法的好坏？

事后统计法
正确性，可读性，健壮性（对不合理输入的反应能力和处理能力）
时间复杂度：估计指令的执行次数
空间复杂度：所占用的存储空间

	public static void test6(int n) {
		// log5(n)
		// O(logn)
		while ((n = n / 5) > 0) {
			System.out.println("test");
		}
	}
		public static void test7(int n) {
		// O(nlogn)
		for (int i = 1; i < n; i += i) {//log2(n)
			for (int j = 0; j < n; j++) {
				System.out.println("test");//n
			}
		}
	}

大O表示法

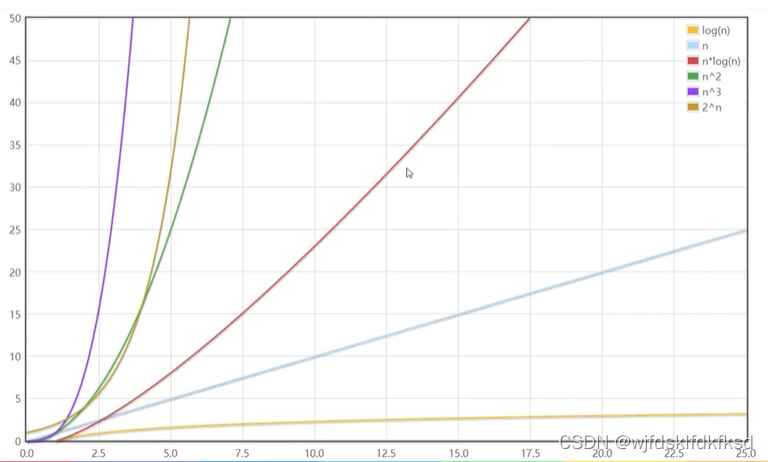
一般用大O表示法来描述复杂度，表示的是数据规模n对应的复杂度。忽略常数，系数，低阶，对数阶省略底数。
例如:
16 … O(1)
2n+1 …O(n)
$n^2+2n+\mathrm{6...............................}$ $O(n^2)$

递归版的斐波那契数算法的时间复杂度分析

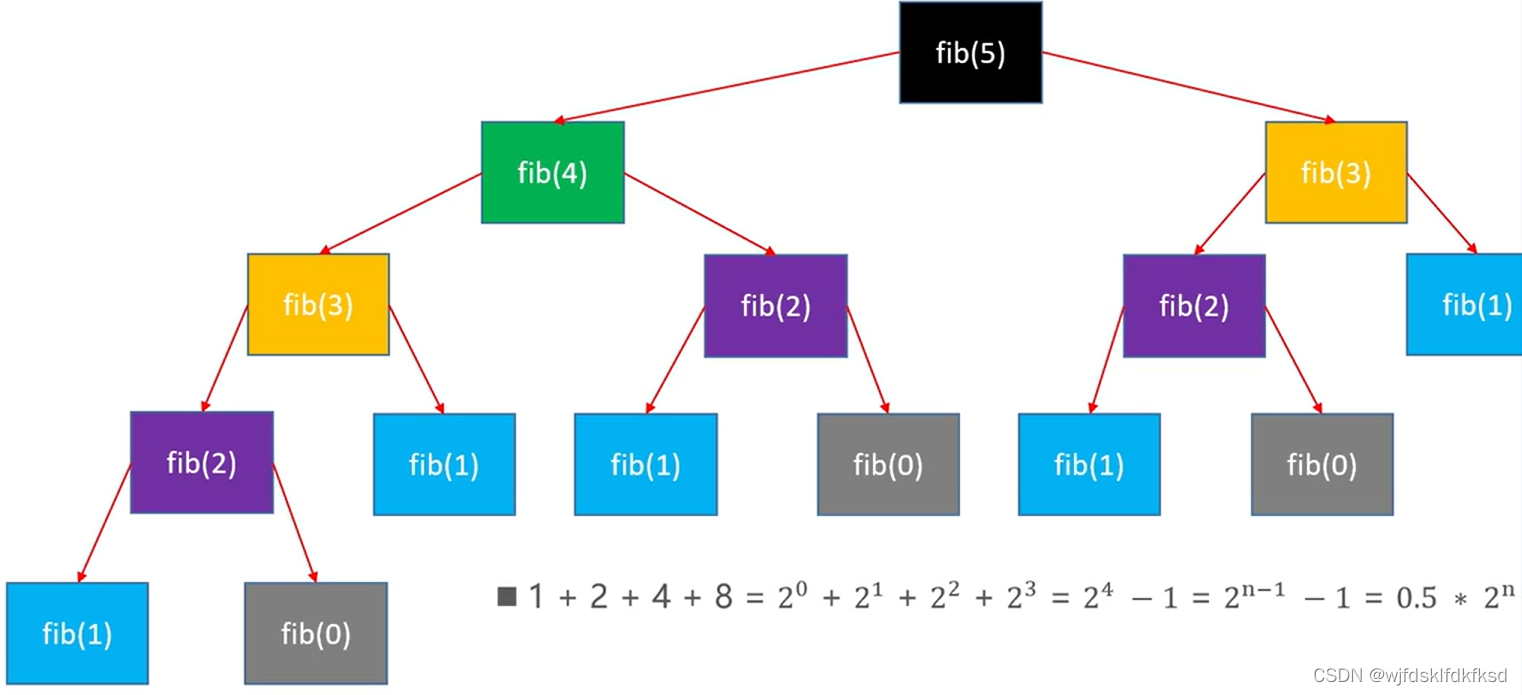
按照每层计算，第一层1，第二层2，第三层4，第四层8，等比数列求和得$0.5\ast 2^n-1$,时间复杂度为$O(2^n)$