文章目录
- 前言
- 🌟一、常见的排序算法:
- 🌟二、选择排序---直接选择排序:
- 🌏2.1.1 基本思想:
- 🌏2.1.2 直接选择排序:
- 🌏2.1.3 直接选择排序的特性总结:
- 🌏2.1.4 思路:
- 🌏2.1.5 代码:
- 🌏2.1.6 注意易错点:
- 🌟三、交换排序---快速排序(上):
- 🌏3.1.1 基本思想:
- 🌏3.1.2 快速排序
- 💫3.1.2.1 第一种---挖坑填补法:
- 📒思路:
- 📒代码:
- 📒流程图:
- 📒时间复杂度:
- 🔑最好的情况:接近二分
- 🔑最坏的情况:有序
- 📒解决方法:三数取中---解决了快排中最坏的情况
- 🔑代码:
- 📒补充知识点:>>1与/2的关系
- 📒小区间优化:
- 🔑代码:
- 😽总结
前言
👧个人主页:@小沈熬夜秃头中୧⍤⃝❅
😚小编介绍:欢迎来到我的乱七八糟小星球🌝
📋专栏:算法
🔑本章内容:选择排序中的直接选择排序和交换排序中的快速排序
送给各位💌:你被黑暗敲打恰恰说明你是光明本身
记得 评论📝 +点赞👍 +收藏😽 +关注💞哦~
提示:以下是本篇文章正文内容,下面案例可供参考
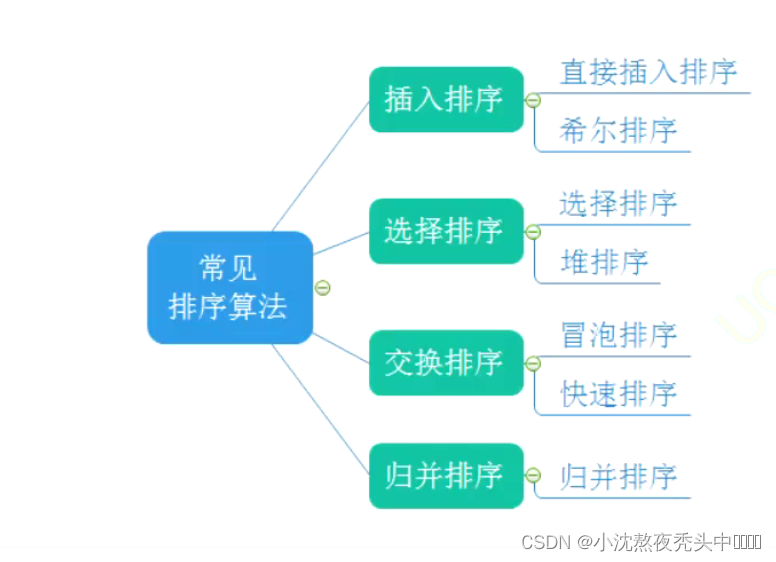
🌟一、常见的排序算法:
前面的插入排序可以回顾【算法】— 几分钟带你走进排序算法大门(上)
选择排序中的堆排序可以回顾【数据结构】—堆排序+TOP-K问题(了解游戏排行底层原理)
交换排序中的冒泡排序可以回顾C-指针的进阶(下)+qsort库函数
所以本章讲解选择排序中的直接选择排序和交换排序中的快速排序
🌟二、选择排序—直接选择排序:
🌏2.1.1 基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
🌏2.1.2 直接选择排序:
- 在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素
- 若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
- 在剩余的array[i]–array[n-2](array[i+1]–array[n-1])集合中,重复上述步骤,直到集合剩余1个元素
🌏2.1.3 直接选择排序的特性总结:
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
🌏2.1.4 思路:
遍历比较选取一个最大的数,一个最小的数,将最小的数和开始位置值交换,最大的数和末尾位置值交换。
🌏2.1.5 代码:
#include<stdio.h>
void Swap(int* p1, int* p2)
{
int* tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int mini = begin, maxi = begin;
for (int i = begin; i <= end; i++)
{
if (a[i] < a[mini])
{
mini = i;
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
Swap(&a[begin],& a[mini]);
if (begin == maxi)
{
maxi = mini;
}
Swap(&a[maxi],& a[end]);
begin++;
end--;
}
}
int main()
{
int a[] = { 9,5,1,7,4,2,6,8
,0,8 };
int n = sizeof(a)/sizeof(a[0]);
SelectSort(a, n);
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
return 0;
}
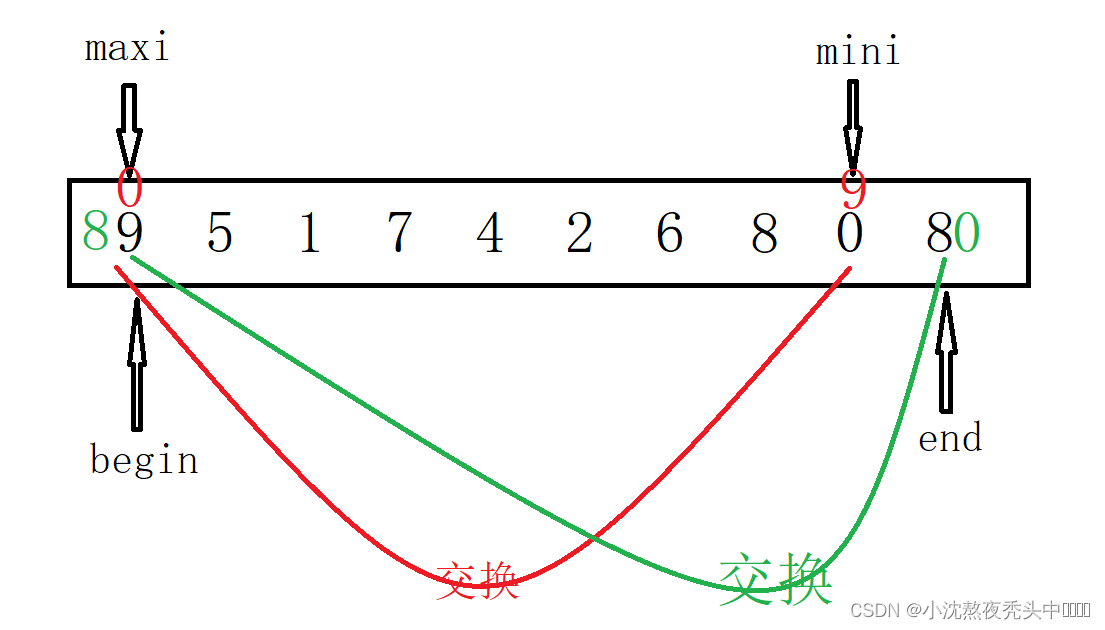
🌏2.1.6 注意易错点:
这一部分是必须要加上的,不然会出现一个bug,当交换开始位置值与最小值之后,要想一下若最大值就是开始位置值,再交换最大值和末尾值那最大值已经和最小值位置交换了不懂可以看下图:
Swap(&a[begin],& a[mini]);
if (begin == maxi)
{
maxi = mini;
}
Swap(&a[maxi],& a[end]);
begin++;
end--;
🌟三、交换排序—快速排序(上):
🌏3.1.1 基本思想:
所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
🌏3.1.2 快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
💫3.1.2.1 第一种—挖坑填补法:
📒思路:
快速排序算法是基于分治策略的另一个排序算法。
该方法的基本思想是:
1.先从数列中取出一个数作为基准数,记为key。
2.分区过程,将小于key的数全放到它的左边,大于key的数全放到它的右边。
📒代码:
#include<stdio.h>
void QuickSort(int* a,int left ,int right)
{
//剩下一个数或者没有数就达到了排序就不用排了
if (left >= right)
{
return;
}
int begin = left, end = right;
int pivot = begin;
int key = a[begin];
while (begin < end)
{
//右边找小,放到左边
while (begin < end && a[end]>=key)
{
end--;
}
//找到放在左边的坑里
a[pivot] = a[end];
pivot = end;
//左边找小,放到右边
while (begin < end && a[begin] <= key)
{
begin++;
}
a[pivot] = a[begin];
//找到放在右边的坑里
pivot = begin;
}
//相遇了
pivot = begin;
a[pivot] = key;
//分治策略,分区间将key左边和右边分别再次找关键key然后再次左小右大
//直到剩下一个数或者没有数就达到了排序的目的
QuickSort(a, left, pivot - 1);//注意传递的区间
QuickSort(a, pivot +1,right);//注意传递的区间
}
int main()
{
int a[] = { 9,5,1,7,4,2,6,3,0,8 };
int n = sizeof(a) / sizeof(a[0]);
QuickSort(a, 0,n-1);
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
return 0;
}
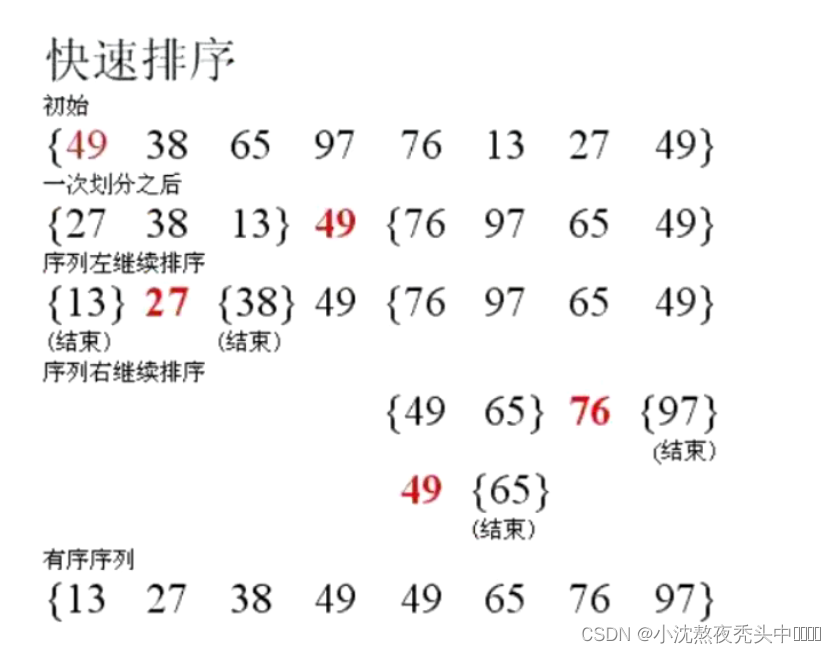
📒流程图:
然后再分为左区间,右区间然后再从左区间中找关键数字再次进行下图这种流程,右区间同理就类似二叉树
📒时间复杂度:
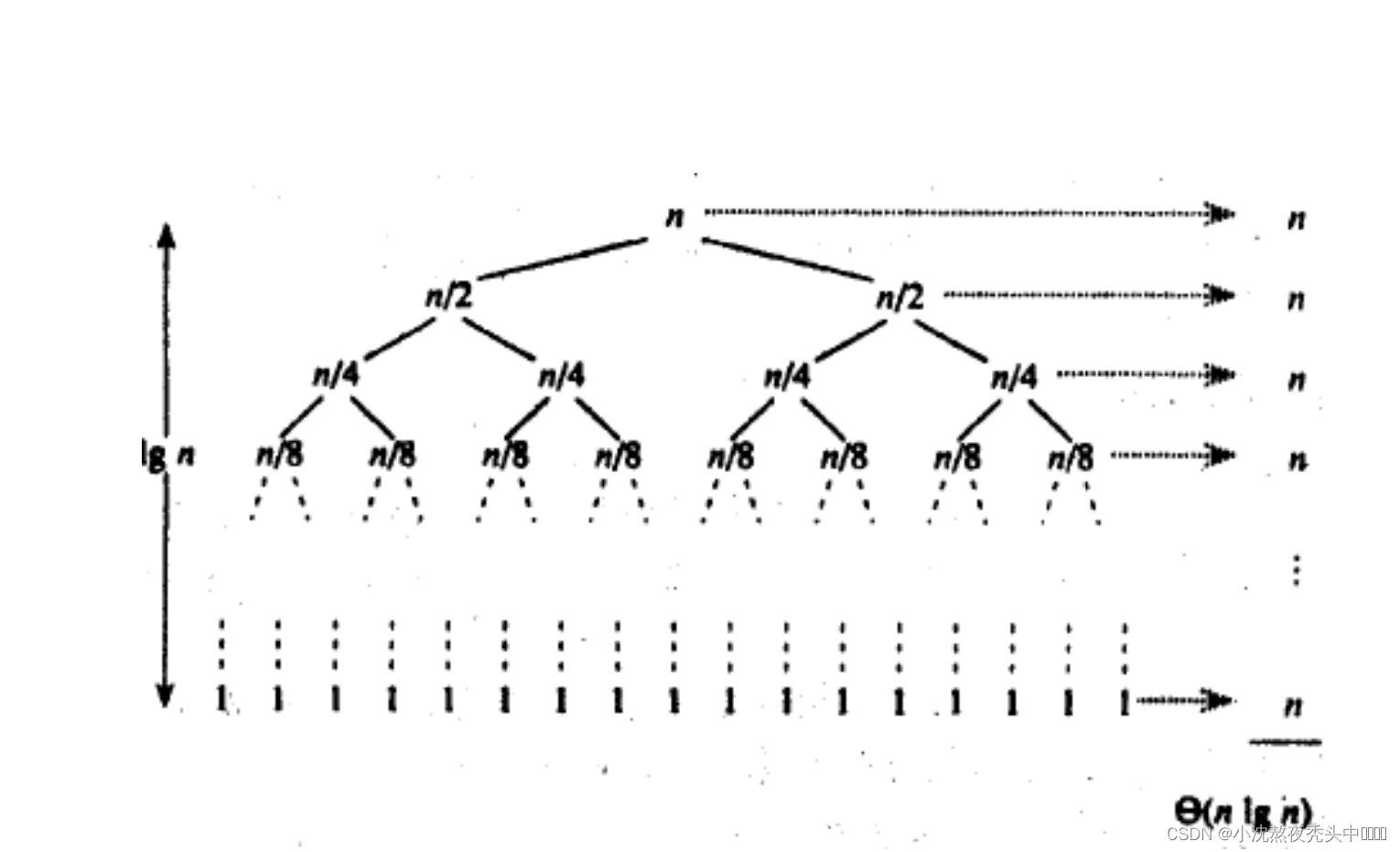
🔑最好的情况:接近二分
快排最好的情况就是二分(选取的key值正确位置刚好接近中间位置):每一次将一个数排到正确位置,分治算法就相当于一个完全二叉树高度为logN,且每一次时间复杂度O(N),所以总共时间复杂度是O(NlogN)*
🔑最坏的情况:有序
快排最坏情况就是有序:当有序时选取最左边(最右边)的数那么都小于(大于)其他数,就会出现左边(右边)没有要排的数,这样每一次都只排一个不像上面的情况类似一个二叉树
📒解决方法:三数取中—解决了快排中最坏的情况
🔑代码:
#include<stdio.h>
void Swap(int* p1, int* p2)
{
int* tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
int GetMidIndex(int* a, int left, int right)
{
int mid = (left + right) >> 1;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else//a[left]>a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}
void QuickSort(int* a,int left ,int right)
{
//剩下一个数或者没有数就达到了排序就不用排了
if (left >= right)
{
return;
}
int index = GetMidIndex(a, left, right);
Swap(&a[left], &a[index]);
int begin = left, end = right;
int pivot = begin;
int key = a[begin];
while (begin < end)
{
//右边找小,放到左边
while (begin < end && a[end]>=key)
{
end--;
}
//找到放在左边的坑里
a[pivot] = a[end];
pivot = end;
//左边找小,放到右边
while (begin < end && a[begin] <= key)
{
begin++;
}
a[pivot] = a[begin];
//找到放在右边的坑里
pivot = begin;
}
//相遇了
pivot = begin;
a[pivot] = key;
//分治策略,分区间将key左边和右边分别再次找关键key然后再次左小右大
//直到剩下一个数或者没有数就达到了排序的目的
QuickSort(a, left, pivot - 1);
QuickSort(a, pivot +1,right);
}
int main()
{
//int a[] = { 0.1,2,3,4,5,6,7,8,9 };
int a[] = { 9,5,1,7,4,2,6,3,0,8 };
int n = sizeof(a) / sizeof(a[0]);
QuickSort(a, 0,n-1);
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
return 0;
}
📒补充知识点:>>1与/2的关系
- n为非负数时,>> 1和/ 2的结果是一样的
- n为负数且还是偶数时,>> 1和/ 2的结果是一样的
- n为负数且还是奇数时,>> 1和/ 2的结果是不一样的
📒小区间优化:
🔑代码:
当每次调用越到最后递归调用越多,所以可以将最后几层递归调用消除掉,越到最后所排序的区间越小所以采用直接插入排序接可以了
对于直接插入排序可以回顾【算法】— 几分钟带你走进排序算法大门(上)
if (pivot - 1 - left > 10)
{
QuickSort(a, left, pivot - 1);
}
else
{
InsertSort(a + left, pivot - 1 - left + 1);
}
if (right-(pivot+1) > 10)
{
QuickSort(a, pivot + 1, right);
}
else
{
InsertSort(a + pivot+1, right-(pivot+1) + 1);
}
😽总结
😽Ending,今天的直接选择排序+快排(中)的内容就到此结束啦~,如果后续想了解更多,就请关注我吧,一键三连哦 ~