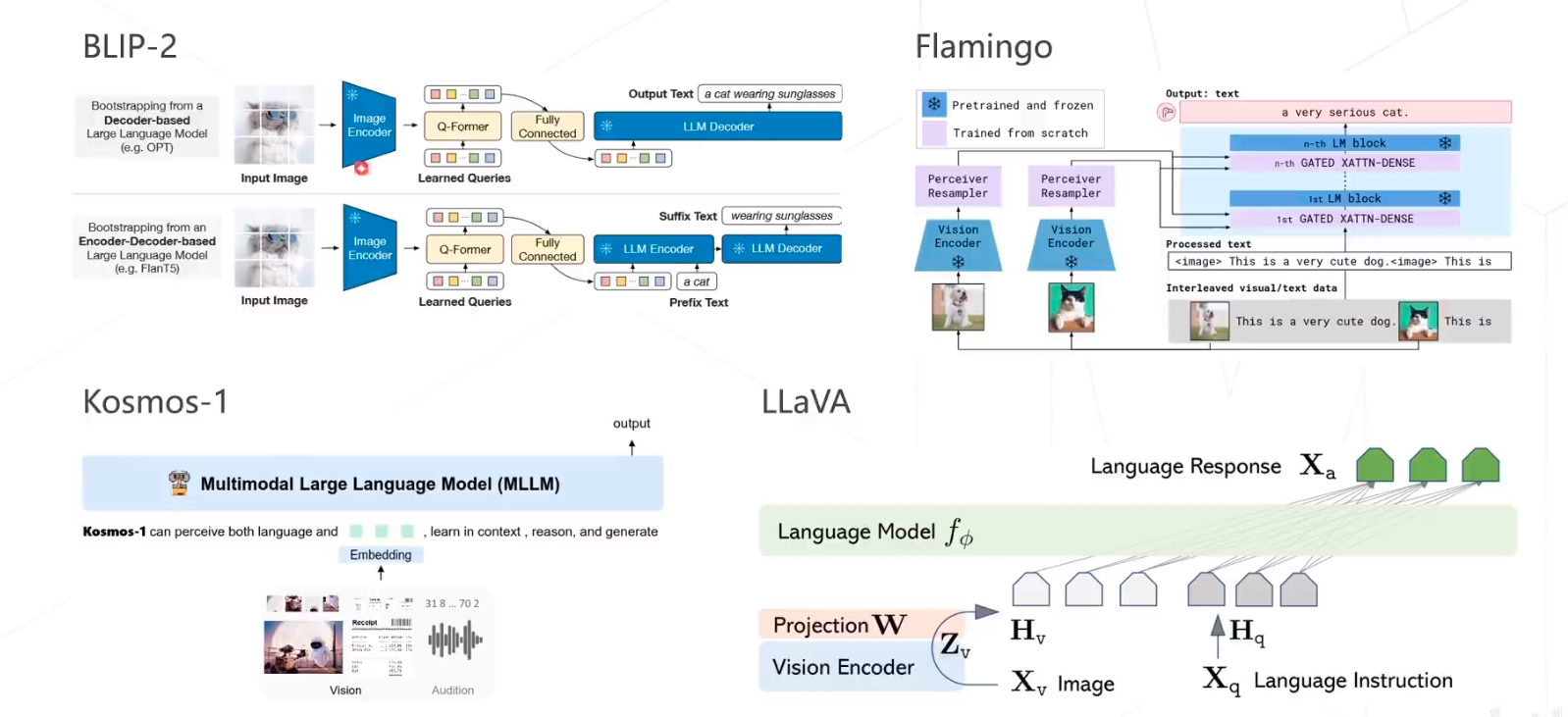
概述

$$Y={\beta }_1{X}_1+{\beta }_2{X}_2+{ϵ}_i$$
边际效应：就是系数，即${\beta }_1$ 、${\beta }_2$
解释：如，在控制其他变量（条件）不变的情况下，每增加一个单位的$X_1$，$Y$增加${\beta }_1$ 个单位。

Probit

模型：

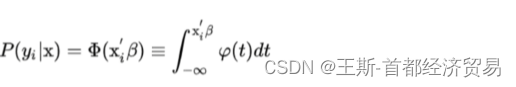
它的边际效益推导：

Probit模型的边际效应可以通过计算变量对概率密度函数的一阶偏导数来获取。具体来说，对于一个二进制（0/1）的因变量$y$，Probit模型可以表示为：

$$P(y=1|x)=\Phi ({\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_k{x}_k)$$

其中，$\Phi ()$是标准正态分布函数。则$x_j$的边际效应为：

$$\frac{\partial P(y=1|x)}{\partial x_j}=\varphi ({\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_k{x}_k)\cdot {\beta }_j$$

其中，$\varphi ()$是标准正态分布的概率密度函数。这个结果告诉我们，边际效应是指当其他变量不变时，增加自变量$x_j$一个单位对因变量的概率影响，即${\beta }_j$。需要注意的是，由于Probit模型是非线性的，所以边际效应可能会随着$x_j$的变化而变化。

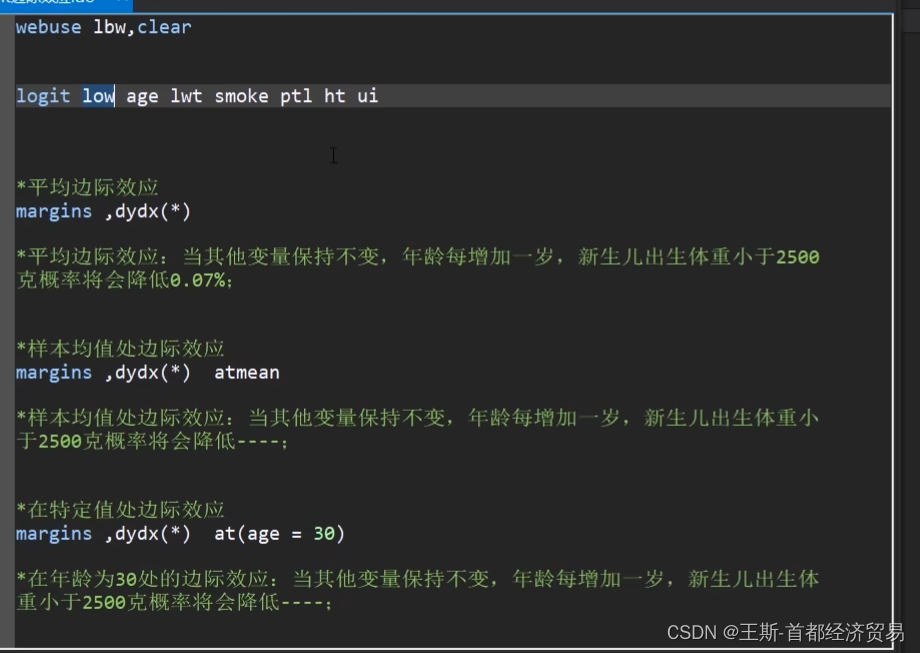
*表示展示所有的变量的边际取值
atmean在样本均值的边际效应
at(age=30)在特定值边际效应的取值

Logit

模型：

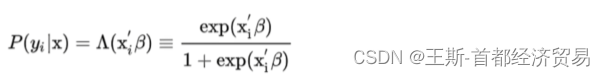
1、只做一次probit模型 
命令：probit y x1 x2,nolog 
mfx compute 
outreg2 using myfile, word replace(导出的是回归系数)
outreg2 using myfile, word mfx ctitle(mfx) append(导出的是边际效应，若不想要回归系数忽略上条命令)
2、做多次probit（因为我是分别加入控制变量和调节变量的，所以我做了两次probit）
probit y x1 x2,nolog 
mfx compute
outreg2 using myfile, word mfx ctitle(mfx) append
probit y x1 x2 x3 x4,nolog 
mfx compute
outreg2 using myfile, word mfx ctitle(mfx) append
注意每次做完probit回归都要做mfx命令和outreg2命令，最后结果就是多次probit的边际效应在一个表里

延伸阅读

这篇知乎文章写得很好
【传送门-二元Logit模型和Probit模型及其Stata实现】作为笔记，码住

IV-Probit

这部分的模型延伸，其实最难的还是找IV，可以参是从地理因素、环境、气候等。
代码：
y:被解释变量
age age_2 sex minzu hukou marry edu pary:控制变量
z:工具变量，可在后面加IV
x:核心解释变量

原理：
见文章：二值选择模型内生性检验方法、步骤及Stata应用

IV-Logit

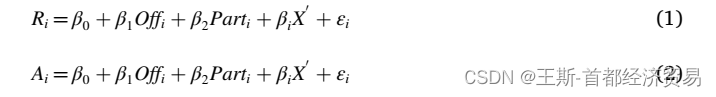
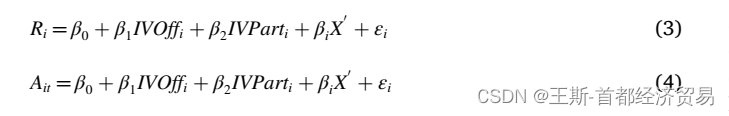
从参考的文献来看，IV-Logit与Logit的区别就是引入工具变量的区别。