1 概述

2 定点数

2.1 表示方法

定点数	描述
定点整数	纯整数。约定小数点在有效数值位之后
定点小数	纯小数。约定小数点在符号位之后，有效数值位之前

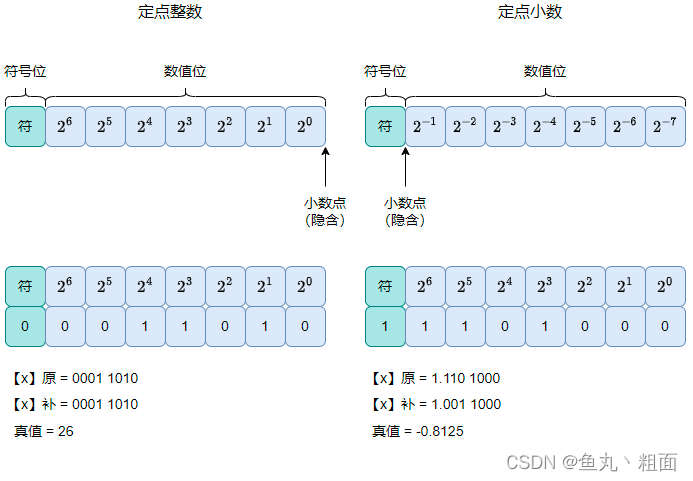
在这里插入图片描述

说明：
① 符号位：0 表示正数，1 表示负数
② 隐含：计算机并不存储小数点，此处的小数点是逻辑概念，故称为隐含
③ 补码：计算机中的数据以补码的形式进行存储

2.2 取值范围

码制	定点整数		定点小数
码制	最小值	最大值	最小值	最大值
原码	-(2^n-1 - 1)	+(2^n-1 - 1)	-(1 - 2^-(n-1))	+(1 - 2^-(n-1))
反码	-(2^n-1 - 1)		-(1 - 2^-(n-1))
补码	-2^n-1		-1
移码	-2^n-1		-1

取值范围理解：当 n = 8 时
定点整数：
   ① 最小值为：1111 1111 = $2^{n-1} - 1)$
   ② 最大值为：0111 1111 = $2^{n-1} - 1)$
   ③ 补码、移码的最小值为：1000 0000 = -128 = $2^{n-1})$ // 特殊
定点小数：
   ① 最小值为：1.111 1111 = $-(2^{-1} + 2^{-2} + 2^{-3} + ... + 2^{-(n-1)}) = - \frac{\frac{1}{2}(1 - \frac{1}{2}^{n-1})}{1 - \frac{1}{2}} =-(1 - 2^{-(n-1)})$ (等比数列)
   ② 最大值为：0.111 1111 = $1 - 2^{-(n-1)})$
   ③ 补码、移码的最小值为：1.000 0001
注意：
   ① 以上最小值，最大值，都是转成原码后，进行比较的
   ② 补码比原码、反码多一个 1000 0000 = --128 唯一特殊
   ③ 计算机中是以补码进行存储的
   ④ 原码和反码取值范围一样，补码和移码取值范围一样，可参考下表

码制	定点整数					定点小数
	负数		0	正数		负数		正数
	最小值	最大值	取值	最小值	最大值	最小值	最大值	最小值	最大值
原码	1111 1111 = -(2 ⁷-1)	1000 0001 = -1	1000 0000 = -0 0000 0000 = +0	0000 0001 = +1	0111 1111 = +(2 ⁷-1)	1.111 1111 = -(1-2^-7)	1.000 0001 = -2^-7	0.000 0001 = 2^-7	0.111 1111 = 1 - 2^-7
补码	1000 0000 = -2 ⁷	1111 1111 = -1	0000 0000 = +0 = 0	0000 0001 = +1	0111 1111 = +(2 ⁷-1)	1.000 0001 = -1	1.111 1111 = -2 ^-7	0.000 0001 = 2^-7	0.111 1111 = 1 - 2^-7

2.3 运算方法

运算	符号	说明
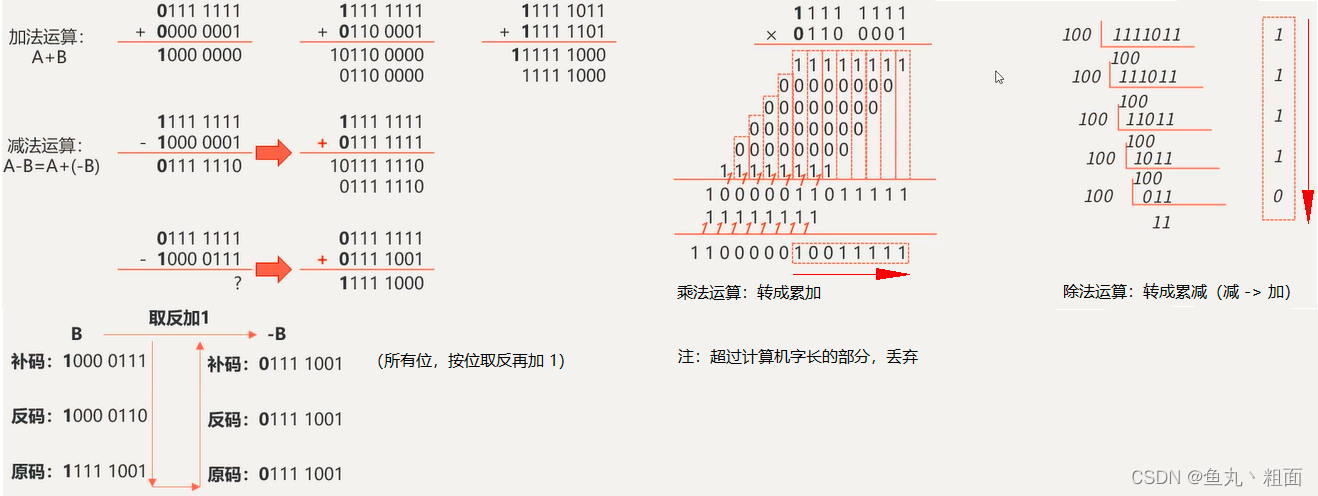
算术运算	加（+）	以 + 为主，减(-)、乘(x)、除(/) 可转换为 +
逻辑运算	与（&）	有 0 为 0，全 1 为 1
	或（\|）	有 1 为 1，全 0 为 0
	非（!）	0 变 1，1 变 0
按位运算	按位与（&）	有 0 为 0，全 1 为 1
	按位或（\|）	有 1 为 1，全 0 为 0
	按位取反（~）	0 变 1，1 变 0
	按位异或（^）	相同为 0，不同为 1
	左移（<<）	向左平移，右边补 0
	右移（>>）	向右平移，左边补符号位
	无符号右移（>>>）	向右平移，左边补 0

在这里插入图片描述

3 浮点数

3.1 表示方法

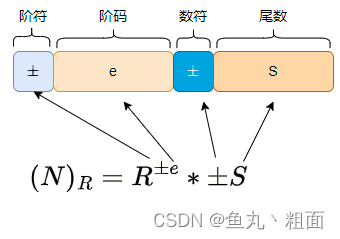
任何一个 R 进制数 N，可以表示为： $(N)_R =\pm S * R^{\pm e}$
- S：尾数。N 的有效数字，反映了数的精度，常用补码表示的 定点小数
- R：基值。即进制数，2、8、10、16 等，常用 2
- e：阶码。小数点的实际位置，反映了数的范围，常用补码表示的 定点整数
- $\pm$ ：阶符、数符。表示符号位。0：正数，1：负数。
$N)_2 = 1101.1001 = 0.11011001 * 2^{100}$
- 尾数 S：11011001
- 基值 R：2
- 阶码 e：100，也就是十进制数 4（可以理解为小数点向左移动 4 位）

3.2 运算方法

顺序	步骤	描述
1	对阶	使阶码相等（小 -> 大），也就是让两个数的数量级相同
2	尾数求和/差
3	规格化	尾数的最高数值位必须有效（非 0）
4	舍入	截断法（恒舍法）：强制舍去 0 舍 1 入法：舍弃位的最高位为 1，则进 1 恒置 1 法：末位恒置 1
5	判断溢出	阶码上溢：异常阶码下溢：作 0