目录

1、什么是Top-K问题？

1.1 Top-K基本思路

2、Top-K问题逻辑分析

2.1 建堆，大小为K的小堆

2.2 将剩余的N - K 个元素依次与堆顶元素比较，大于就替换

2.3 打印堆

3、TopK实现代码

4、Top-K问题完整代码

结果展示：

---

TopK问题的引入：
大家在玩王者荣耀的时候都遇到过xxx市第xxx某英雄，xxx区第xxx某英雄。或者是今天我们点外卖的时候想吃某个食物，我们打开美团/饿了么，选离自己最近的选项或者评分最高的选项就会将你所选的店铺的前x名按顺序排出来。福布斯排行榜前10名，胡润富豪排行榜前5名等等。这些问题都是需要对大量的数据排序，选出最大的前K个，这里就用到了TopK算法来解决这一类问题。

1、什么是Top-K问题？

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能
数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：

1.1 Top-K基本思路

（1）用数据集合中前K个元素来建堆
        如果是前k个最大的元素，则建小堆
        如果是前k个最小的元素，则建大堆

（2）用剩余的N-K个元素依次与堆顶元素来比较（我们这里求前K个最大为例），我们是建小堆，所以堆顶元素是这个小堆中最小的，因此我们就从剩下的N-K个元素第一个开始与堆顶比较，如果大于堆顶元素，就将堆顶元素替换掉，并向下调整重建小堆，如果小于堆顶元素就不替换，让下一个元素与堆顶比较，剩下的N-K个元素依次比较，重复此步骤。
（3）将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

2、Top-K问题逻辑分析

（1）先用前K个建小堆；

（2）将剩余的N - K 个元素依次与堆顶元素比较，大于就替换；

（3）打印堆。

这是我们的大逻辑，我们将这三步一步步的来分析：

2.1 建堆，大小为K的小堆

过程：

1.我们先开辟一个大小为k的空间；

2.将前K个数据向下调整建成小堆。（向下调整建堆不明白的小伙伴可以戳这里复习）

代码如下：

int* kminheap = (int*)malloc(sizeof(int) * k);
if (NULL == kminheap)
{
    perror("malloc fail:");
    return;
}

for (int i = 0; i < k; i++)
{
    fscanf(fout, "%d", &kminheap[i]);
}

//建小堆
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
{
    AdjustDown(kminheap, k, i);
}

2.2 将剩余的N - K 个元素依次与堆顶元素比较，大于就替换

过程：

1.因为我们是前K个最大数据，所以我们建的是小堆，小堆的堆顶元素就是这个堆中最小的元素，让剩下的N-K个元素依次与堆顶比较；

2.如果这个元素比堆顶大，我们就让它替换掉堆顶元素，如果小于则不交换，依次往后面的元素走再去比较；

3.如果交换了，就从堆顶开始往下调整重新建堆，堆顶就又是最小的元素；

4.当 N-K 个元素依次比较完后，堆中的 K 个元素就是要找的前 K 个最大元素。

代码如下：

int val = 0;
while (!feof(fout))
{
    fscanf(fout, "%d", &val);
    if (val > kminheap[0])
    {
        kminheap[0] = val;
        AdjustDown(kminheap, k, 0);
    }
}

2.3 打印堆

for (int i = 0; i < k; i++)
{
    printf("%d ", kminheap[i]);
}

3、TopK实现代码

void PrintTopK(int k)
{
	const char* file = "data.txt";
	FILE* fout = fopen(file, "r");
	if (NULL == fout)
	{
		perror("fopen error:");
		return;
	}

		int* kminheap = (int*)malloc(sizeof(int) * k);
		if (NULL == kminheap)
		{
			perror("malloc fail:");
			return;
		}

		for (int i = 0; i < k; i++)
		{
			fscanf(fout, "%d", &kminheap[i]);
		}

		//建小堆
		for (int i = (k - 1 - 1) / 2; i >= 0; i--)
		{
			AdjustDown(kminheap, k, i);
		}

	int val = 0;
	while (!feof(fout))
	{
		fscanf(fout, "%d", &val);
		if (val > kminheap[0])
		{
			kminheap[0] = val;
			AdjustDown(kminheap, k, 0);
		}
	}

	for (int i = 0; i < k; i++)
	{
		printf("%d ", kminheap[i]);
	}
	printf("\n");

}

我们这里的代码是从文件中读数据的，我们是将准备的数据存放在文件中。

4、Top-K问题完整代码

我们这是先造1000个数字，将数字存放到一个文件中，求 Top-K 的时候再从文件中拿这些数字。

void CreateNData()
{
	//造数据
	int n = 1000;
	srand((unsigned int)time(NULL));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (NULL == fin)
	{
		perror("fopen error:");
		return;
	}

	for (size_t i = 0; i < n; i++)
	{
		int x = rand() % 100000;
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}
void PrintTopK(int k)
{
	const char* file = "data.txt";
	FILE* fout = fopen(file, "r");
	if (NULL == fout)
	{
		perror("fopen error:");
		return;
	}

		int* kminheap = (int*)malloc(sizeof(int) * k);
		if (NULL == kminheap)
		{
			perror("malloc fail:");
			return;
		}

		for (int i = 0; i < k; i++)
		{
			fscanf(fout, "%d", &kminheap[i]);
		}

		//建小堆
		for (int i = (k - 1 - 1) / 2; i >= 0; i--)
		{
			AdjustDown(kminheap, k, i);
		}

	int val = 0;
	while (!feof(fout))
	{
		fscanf(fout, "%d", &val);
		if (val > kminheap[0])
		{
			kminheap[0] = val;
			AdjustDown(kminheap, k, 0);
		}
	}

	for (int i = 0; i < k; i++)
	{
		printf("%d ", kminheap[i]);
	}
	printf("\n");

}

结果展示：

快速验证技巧：我们这里是写到文件里面了，我们为了快速验证代码是否写正确调用一遍生成数据的接口，然后将它注释掉，进到data.txt文件中改五个最大的数据出来，再去打印，这样就能快速验证。

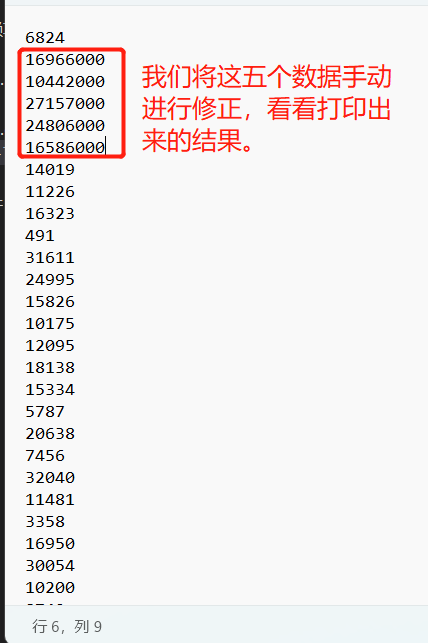
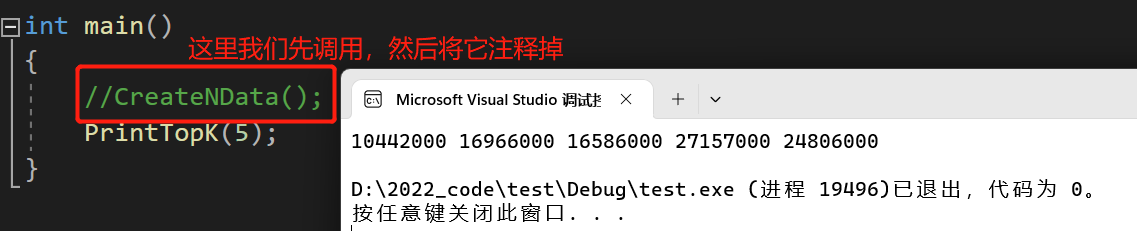
对比两张图片，打印出来的就是前 5 个最大的值。

*** 本篇完 ***