辐射的频谱分析

• 韧致辐射就是带电粒子入射到物质靶上时，它和靶内原子中的电子和原子核碰撞，在碰撞过程减速而产生的辐射。X射线的连续谱部分就体现了韧致辐射的性质。在这个过程中的带电粒子速度远小于光速

低速运动带电粒子在碰撞过程中的辐射频谱

• 频谱形式的电场强度公式

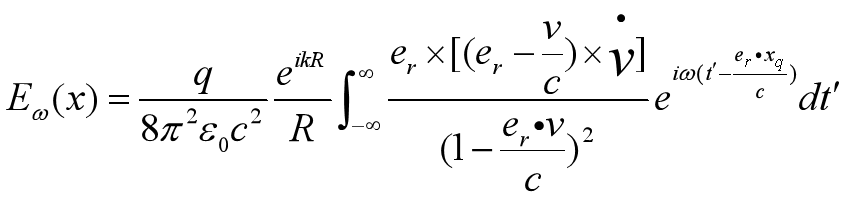
• 粒子在很短的时间τ内减速
  • ω>>1/τ时
    • W_ω≈0 (ωτ≫1)
  • ω<<1/τ时
    • E_ω(x)=q/8π^2ε_0c^2e^ikR/R∫_−∞^∞e_r×(e_r×v ̇)exp(iωt’)dt’
    • ≈q/8π^2ε_0c^2e^ikR/Re_r×(e_r×∆v) (ωτ≪1)
• 设e_r与∆v的夹角为Θ，则易知e_r×(e_r×∆v)在数值上等于|∆vsinΘ|，则带入已经求得的频率为ω的单位频率间隔辐射能量角分布有dW_ω/dΩ=q^2/16π^3ε_0c^3|∆v|^2sin^2Θ;W_ω=q^2/6π^2ε_0c(∆v/c)^2

高速圆周运动带电粒子的辐射频谱

• 设有一个高速运动(v≈c)的带电粒子在做圆周运动.在每一瞬间粒子产生的辐射都集中于沿v方向的狭窄射束内，射束的张角~1/γ
• 当粒子做圆周运动时，在远处某一点P观察，粒子每旋转一周时的射束只在一个短时间∆t内扫过，是一个周期性的脉冲波形
• 设轨道半径为ρ，粒子走过路程ρ∆θ的时间为∆t^′=ρ∆θ/v~ρ/cγ
• 在P点上观察到脉冲的持续时间为∆t=(dt/dt^′)∆t′
  • dt/dt^′=1−v/ccosθ≈1/2(1/γ^2+θ^2)-->∆t~ρ/cγ^3
• 当脉冲时间为∆t时，频谱主要分布区域ω≤ω_c~1/∆t~c/ργ^3=ω_0γ^3