在自然语言处理（NLP）中，语言模型（Language Models）是用来预测文本序列中下一个单词或者字符的概率分布的模型。语言模型的主要目标是捕捉语言的统计规律，以此来生成自然语言。以下是一些常见的语言模型：

• N-gram Language Model: 这是最早的语言模型之一，主要用于捕捉词序列中的n-1阶依赖关系。然而，N-gram模型对于长距离依赖的处理不佳，且模型大小随着n的增大而急剧增大。

• Hidden Markov Model (HMM): HMM是一种统计模型，用于描述一个含有未知参数的马尔可夫过程。在NLP中，HMM常被用于词性标注和命名实体识别等任务。

• Recurrent Neural Networks (RNNs): RNNs可以捕捉序列数据中的长距离依赖关系，尤其是LSTM和GRU等变体，在处理包含长序列的语言数据时表现出色。

• Transformers and Attention Mechanisms: Transformers模型使用自注意力（Self-Attention）机制来捕捉输入序列中不同位置之间的依赖关系。最著名的Transformer模型是Google的BERT。

• BERT (Bidirectional Encoder Representations from Transformers): BERT模型改变了语言模型的训练方式，使其能够同时考虑上下文中的前后信息。这让模型在许多NLP任务中都取得了显著的改进。

• GPT (Generative Pretraining Transformer): GPT模型由OpenAI提出，是一种以Transformer为基础的生成式预训练模型。GPT在很多生成性任务，如文本生成，对话系统等方面表现优秀。

• RoBERTa, ELECTRA, T5, BART: 这些都是在BERT和GPT的基础上提出的模型，通过不同的训练策略或模型结构，进一步提升了模型的性能。

这些模型在自然语言处理的许多任务中都取得了良好的效果，包括文本分类、命名实体识别、情感分析、文本生成、机器翻译等等。

N-gram Language Model

• N-gram 语言模型基于马尔科夫假设

马尔科夫假设：

• 马尔科夫假设是指一个词的出现仅依赖于它前面的几个词，而与更早的词或更晚的词无关。在N-gram模型中，这个“几个词”就是N-1个。例如，在一个2-gram（也被称为bigram）模型中，一个词的出现仅依赖于它前面的一个词。在3-gram（也被称为trigram）模型中，一个词的出现依赖于它前面的两个词，以此类推。
• 马尔科夫假设使得N-gram模型的计算变得可行，因为它大大减少了需要计算的条件概率的数量。然而，这个假设也引入了一些限制，最明显的是它不能处理长距离的依赖关系

Trigram Example

$$P(w_i|w_{i-2},w_{i-1})=\frac{C(w_{i-2},w_{i-1},w_i)}{C(w_{i-2},w_{i-1})}$$

• 其中 $C(\cdot )$ 代表的是当前序列的 频次

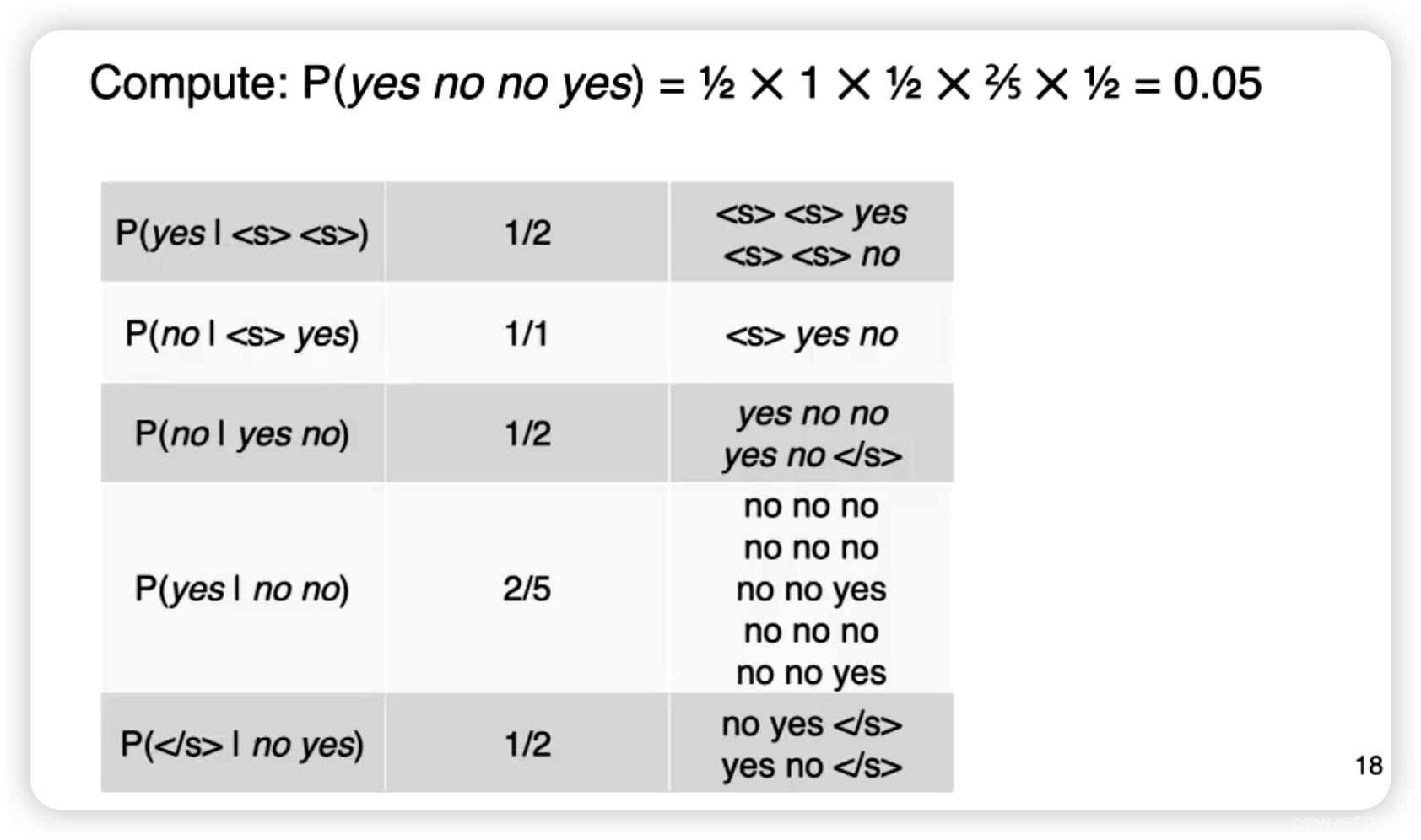
在这个例子中，我们执行几个简单的计算步骤看一下：

• 要计算 $P(yesnonoyes)$ 这个概率，我们需要先计算第一个 yes 在当前 corpus 中的概率，由于我们当前的情景是 3-gram，因此需要在前面增加两个 <s><s> 然后我们统计在 corpus 中：$C(<s><s>yes)$ 的频次是 1
  

• 而 $C(<s><s>)$ 的频次是 2：
  

• 所以第一项 $P(yes|<s><s>)$ 的概率是 $\frac{1}{2}$

• 以此类推，我们重复这个过程直到 </s> 出现的 $P(</s>|noyes)$

• 然后将这些概率连乘起来就得到了整个序列的概率 $P(yesnonoyes)$
  

存在的问题

N-gram 在许多简单应用中表现得很好，但它也有一些显著的缺点：

• 数据稀疏问题： N-gram 模型的性能很大程度上取决于训练数据的质量和数量。如果训练数据中没有出现过某个特定的 N-gram，模型就无法预测它。这就是所谓的数据稀疏问题，也是 N-gram 模型的一个主要限制。

• 长距离依赖问题： N-gram 模型基于马尔可夫假设，即下一个词的出现只依赖于前面的 N-1 个词。这使得模型在处理长距离依赖关系时效果不佳。例如，对于一个长句子，句首的词可能会影响句尾的词，但如果 N 值设置得较小，这种依赖关系就无法被模型捕获。

• 计算和存储需求： 随着 N 的增大，需要计算和存储的 N-gram 的数量会呈指数级增长。这使得 N-gram 模型对计算资源和存储空间的需求很高，特别是对于大规模的语料库。

• 无法学习语义信息： N-gram 是一种基于统计的模型，它无法学习词语之间的深层次语义关系。例如，它无法理解同义词或反义词这样的语义信息。

• 无法处理未知词： 对于训练数据中未出现过的词，N-gram 模型无法处理。这在处理实际文本数据时是一个常见问题，因为语言中总会有新词出现。

smoothing

• 对于 N-gram 来说，最严中的问题就是 未知词 问题，因为 N-gram 的最终的概率值取决于连乘的概率项，而有的项可能为 0，当这种情况出现，整个句子的概率就会为 0， 因此我们需要进行处理。
  

Laplacian （add-one） smoothing

• 在 unigram 的场景下，我们对当前词 w_i 的频次 +1，在分母上我们则加上整个 词表 的大小
  

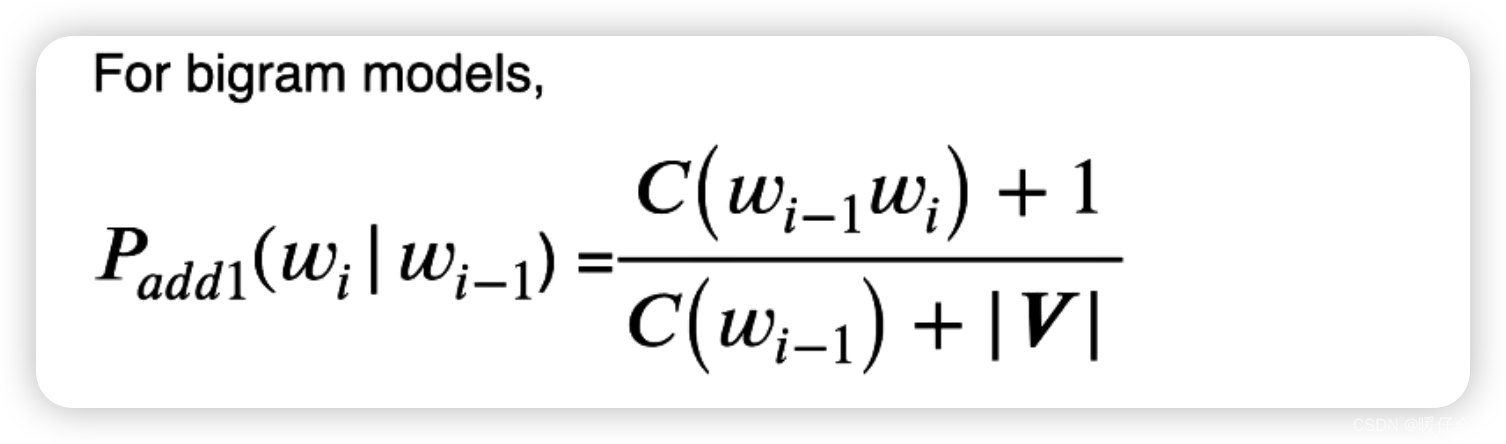
• 在 bigram 的场景下，分子依然 +1，分母依然加整个 词表 的大小

案例 1

• 注意：这里的词表 V中包含了最后一个结束字符 </s> 但是没有包含开始字符 <s>，原因是：
  • 在计算过程中我们几乎总要计算 $P(</s>|w_{i-1}{w}_{i-2}....)$ ，因为我们需要得到 </s> 来表示句子的预测过程结束了，但是我们不会计算 $P(<s>|....)$ 因为这没有意义。
    

案例 2

• 当我们计算 $P(ate|cheese)$ 我们发现 $C(cheeseate)$ 频次为 0，但是由于这时候我们进行了平滑，因此并不会导致概率为 0

Add-k smoothing

• 这里选择 k=0.1，计算出的 smoothed_probability 就是平滑后的概率，计算出平滑后的概率之后我们分别用这些 smoothed_probability 去乘 counts 的总和 20，这样我们可以得到对于任意一个单词，他们的实际有效 count 是多少。
• 例如对于 improperty 来说，实际有效是 7.8 次，而相较于他自己原本的 counts 略微小了一点，但是对于其他的词，例如 outbreak 经过平滑后的 effective_count 是 1.063 比实际的 counts 略大一些。

Absolute Discounting

Absolute Discounting是一种处理数据稀疏问题的平滑技术，广泛应用于N-gram语言模型中。它的基本思想是对训练数据中出现过的N-gram的计数进行绝对减值（一般为一个常数），然后将减少的这部分计数分配给训练数据中未出现过的N-gram。

举个例子，假设我们有一个bigram（2-gram）语言模型，在训练集中， eat apple 的计数是10，那么在absolute discounting下，我们可能将这个计数减少到 9，并将减少的这一计数分配给训练集中未出现过的bigram，如 eat banana。

这种做法的好处在于，它为那些在训练数据中未出现过的N-gram提供了一些非零的概率，从而使模型能够更好地处理那些在测试数据中可能出现但在训练数据中未出现的N-gram，有效地缓解了数据稀疏问题。

案例

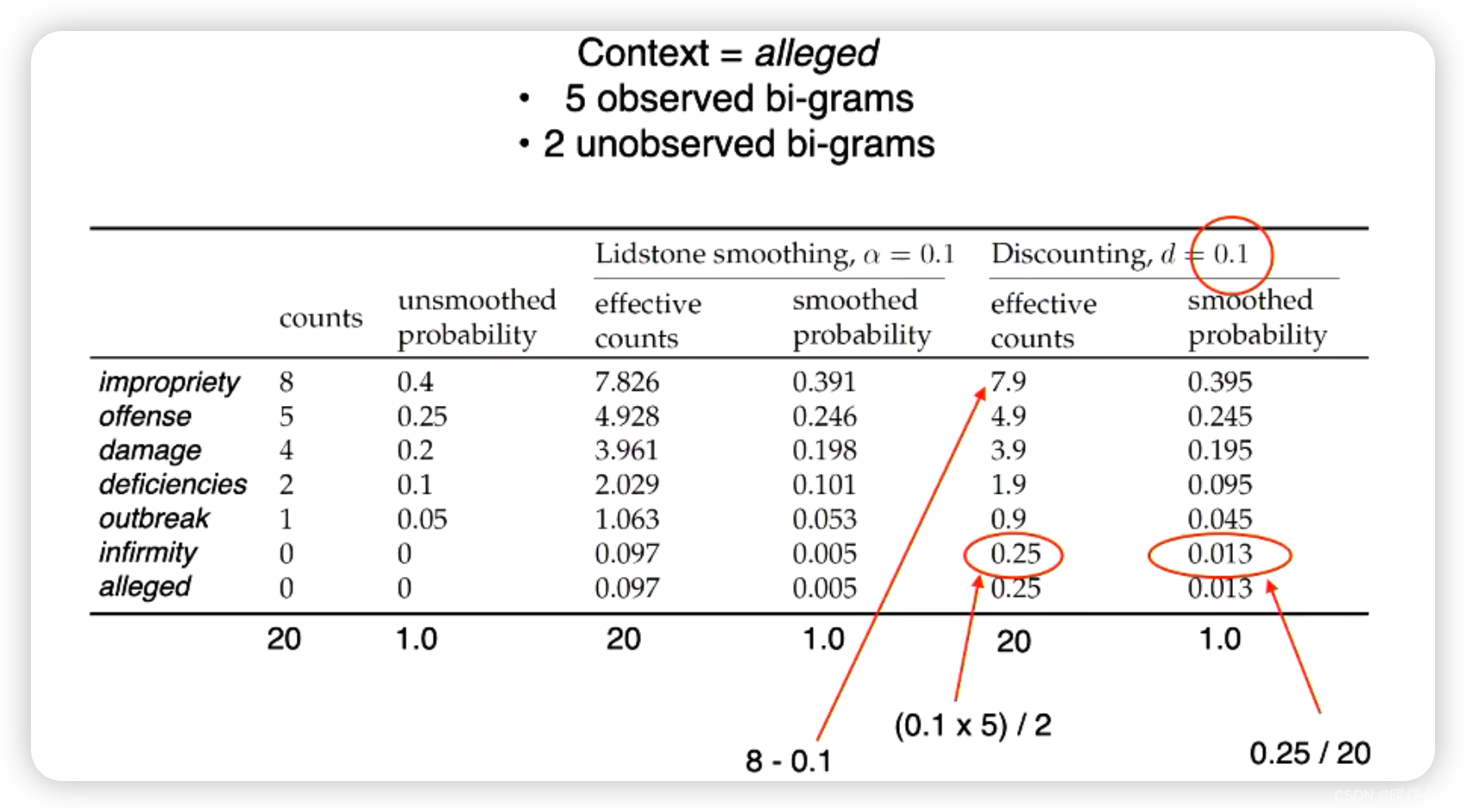
• 在这个例子中， d=0.1 代表所有非零的情况都将实际的 counts - 0.1，图中一共有 5 个非零的词，因此一共得到了 0.5 个富裕的 point
• 图中一共有 2 个 0 的词， 因此平均分配给他们，所以他们的 effective_counts = （5 * 0.1）/ 2 = 0.25
• 由 0.25 的 effective_counts 反推到 smoothed_probability 计算得到其平滑结果是 0.013

但是这种方法的缺点在于：他对于概率为 0 的情况进行分配是平均的，但显然在数据集中对所有未出现的情况取平均是不合理的，一种改进的方法是：重新分配这些 points 的时候，按照他们的 频次 进行权重分配

• 在 Katz Backoff 中，如果一个 N-gram 在训练数据中存在，那么其概率就通过经过一定折扣的频率来计算。然而，如果该 N-gram 在训练数据中不存在，我们就回退到一个低阶的模型。例如，如果一个三元组（trigram）在训练数据中未见过，那么我们就回退到相应的二元组（bigram）模型，如果二元组也未见过，我们甚至可以回退到一元组（unigram）模型。

• 回退到低阶模型的概率分布是基于未被高阶模型使用的概率质量来重新分配的。这种方法使得未在训练数据中见过的 N-gram 能够得到非零概率，从而缓解了数据稀疏性问题。

• 在上面的例子中当 $C(w_{i-1},w_i)>0$ 的时候，采用的是 bigram 的方式进行

（未完。。。。）

Interpolation