下面的图表展示了我们日常生活中最常用的算法。它们被应用在互联网搜索引擎、社交网络、WiFi、手机甚至卫星等各个领域。

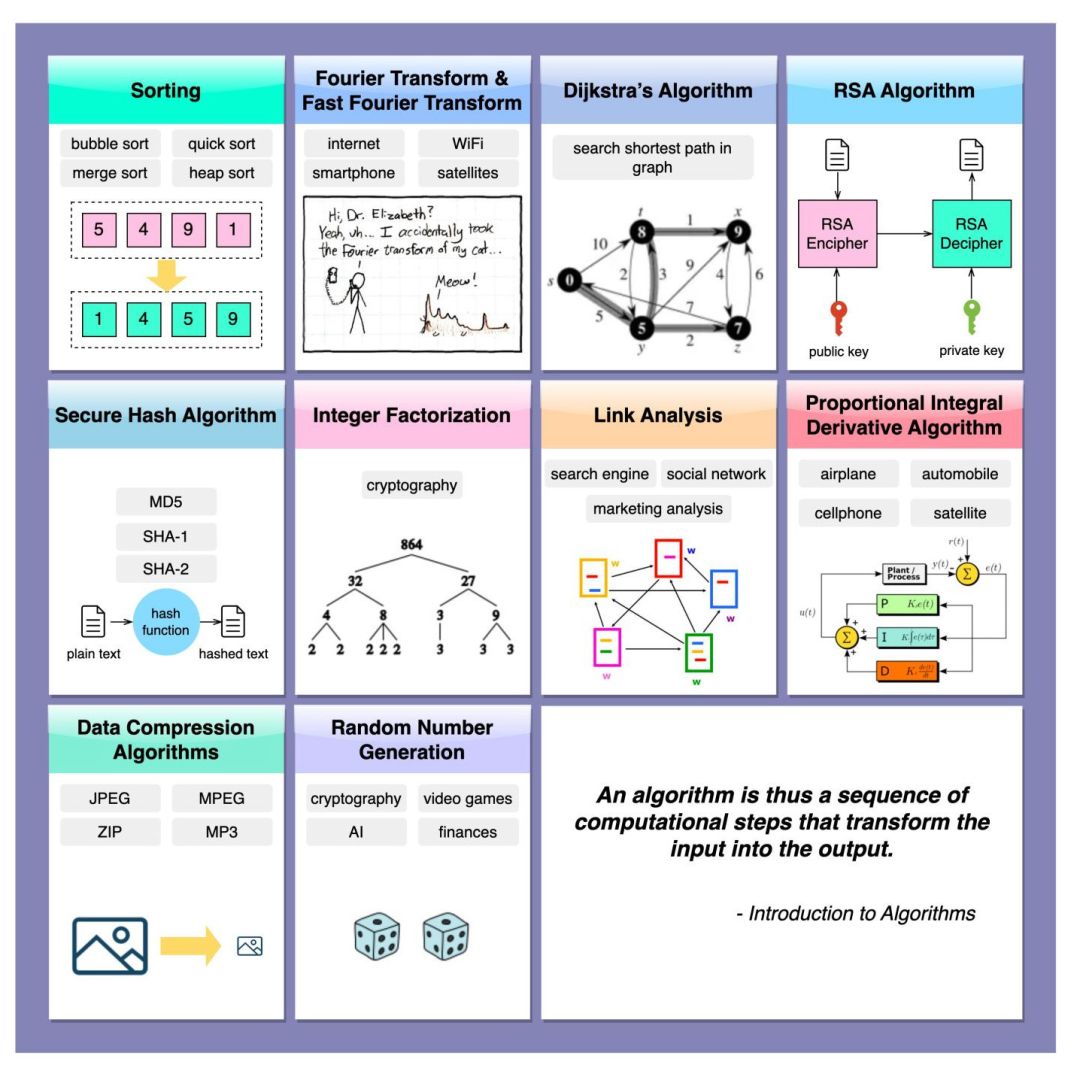
1.排序算法

排序算法用于将一组数据按照特定的顺序进行排列。它们被广泛应用于各种场景，如搜索引擎中的搜索结果排序、数据分析中的数据整理和展示等。

# 冒泡排序
def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr


data = [64, 34, 25, 12, 22, 11, 90]
sorted_data = bubble_sort(data)
print(sorted_data)  # 输出：[11, 12, 22, 25, 34, 64, 90]

2.傅里叶变换与快速傅里叶变换

傅里叶变换用于将一个函数（或信号）从时间域转换到频域，快速傅里叶变换是一种高效计算傅里叶变换的算法。它们在信号处理、图像处理、音频压缩等领域具有广泛应用。

import numpy as np


# 傅里叶变换
def fourier_transform(signal):
    fft_result = np.fft.fft(signal)
    return fft_result


# 快速傅里叶变换
def fast_fourier_transform(signal):
    fft_result = np.fft.fft(signal)
    return fft_result


signal = [0, 1, 2, 3, 4, 5, 6, 7]
fft_result = fourier_transform(signal)
print(fft_result)


fft_result_fast = fast_fourier_transform(signal)
print(fft_result_fast)

3.Dijkstra算法

Dijkstra算法是一种用于求解带权重图中最短路径的算法。它被广泛应用于路由算法、地图导航等场景，用于找到两个节点之间的最短路径。

import sys


# Dijkstra算法
def dijkstra(graph, start):
    distance = {node: sys.maxsize for node in graph}
    distance[start] = 0


    visited = set


()


    while len(visited) < len(graph):
        min_distance = sys.maxsize
        min_node = None


        for node in graph:
            if node not in visited and distance[node] < min_distance:
                min_distance = distance[node]
                min_node = node


        visited.add(min_node)


        for neighbor, weight in graph[min_node].items():
            distance[neighbor] = min(distance[neighbor], distance[min_node] + weight)


    return distance


graph = {
    'A': {'B': 1, 'C': 4},
    'B': {'A': 1, 'C': 2, 'D': 5},
    'C': {'A': 4, 'B': 2, 'D': 1},
    'D': {'B': 5, 'C': 1}
}


start_node = 'A'
shortest_distances = dijkstra(graph, start_node)
print(shortest_distances)

4.RSA算法

RSA算法是一种非对称加密算法，常用于数据加密和数字签名。它基于大整数的因式分解难题，保证了加密的安全性。

from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP


# 生成RSA密钥对
key = RSA.generate(2048)
private_key = key.export_key()
public_key = key.publickey().export_key()


message = b'Hello, World!'


# 使用公钥加密
cipher_rsa = PKCS1_OAEP.new(RSA.import_key(public_key))
encrypted_message = cipher_rsa.encrypt(message)


# 使用私钥解密
cipher_rsa = PKCS1_OAEP.new(RSA.import_key(private_key))
decrypted_message = cipher_rsa.decrypt(encrypted_message)


print(decrypted_message.decode())  # 输出：Hello, World!

5.安全哈希算法

安全哈希算法用于将任意长度的数据映射为固定长度的哈希值。常见的安全哈希算法有SHA-256、SHA-512等，它们被广泛应用于数据完整性校验、密码存储等场景。

import hashlib


message = b'Hello, World!'


# 计算SHA-256哈希值
hash_value = hashlib.sha256(message).hexdigest()
print(hash_value)


# 计算SHA-512哈希值
hash_value = hashlib.sha512(message).hexdigest()
print(hash_value)

6.整数因式分解

整数因式分解是将一个大整数分解为其素因子的过程。它在密码学中具有重要作用，例如RSA算法的安全性依赖于大整数的难以因式分解性质。

def factorize_integer(n):
    factors = []
    i = 2
    while i * i <= n:
        if n % i:
            i += 1
        else:
            n //= i
            factors.append(i)
    if n > 1:
        factors.append(n)
    return factors


integer = 1234567890
factors = factorize_integer(integer)
print(factors)

7.链接分析

链接分析是一种用于分析网络中节点之间链接关系的算法。它被广

泛应用于搜索引擎的网页排名算法，如PageRank算法。

# 简化的PageRank算法
def pagerank(graph, damping_factor=0.85, max_iterations=100, convergence_threshold=0.0001):
    num_nodes = len(graph)
    initial_score = 1 / num_nodes
    scores = {node: initial_score for node in graph}


    for _ in range(max_iterations):
        prev_scores = scores.copy()
        convergence = 0


        for node in graph:
            score = (1 - damping_factor) / num_nodes


            for neighbor in graph:
                if node in graph[neighbor]:
                    score += damping_factor * prev_scores[neighbor] / len(graph[neighbor])


            scores[node] = score
            convergence += abs(scores[node] - prev_scores[node])


        if convergence < convergence_threshold:
            break


    return scores


graph = {
    'A': {'B': 1, 'C': 1},
    'B': {'A': 1, 'C': 1},
    'C': {'A': 1, 'B': 1}
}


pagerank_scores = pagerank(graph)
print(pagerank_scores)

8.比例积分微分控制算法

比例积分微分（PID）控制算法是一种常用的反馈控制算法。它根据当前误差、误差积分和误差微分来调节控制器的输出，广泛应用于自动化控制系统中。

class PIDController:
    def __init__(self, kp, ki, kd):
        self.kp = kp
        self.ki = ki
        self.kd = kd
        self.previous_error = 0
        self.integral = 0


    def calculate_output(self, error, dt):
        self.integral += error * dt
        derivative = (error - self.previous_error) / dt
        output = self.kp * error + self.ki * self.integral + self.kd * derivative
        self.previous_error = error
        return output


pid_controller = PIDController(0.5, 0.1, 0.2)
setpoint = 10
dt = 0.01
time = 0
output = 0


while time < 1:
    error = setpoint - output
    output = pid_controller.calculate_output(error, dt)
    time += dt
    print(f'Time: {time}, Output: {output}')

9.数据压缩算法

数据压缩算法用于将数据表示为更紧凑的形式，以减少存储空间或传输带宽的使用。常见的数据压缩算法有Huffman编码、LZ77、LZW等，它们被广泛应用于文件压缩、图像压缩等领域。

import gzip


data = b'Hello, World!'


# 使用gzip进行压缩
compressed_data = gzip.compress(data)
print(compressed_data)


# 使用gzip进行解压缩
decompressed_data = gzip.decompress(compressed_data)
print(decompressed_data.decode())  # 输出：Hello, World!

10.随机数生成

随机数生成算法用于生成

随机的数字或数据序列。在密码学、模拟实验、游戏开发等领域中，随机数生成算法扮演着重要的角色。

import random


# 生成随机整数
random_integer = random.randint(1, 10)
print(random_integer)


# 生成随机浮点数
random_float = random.uniform(0, 1)
print(random_float)


# 从列表中随机选择元素
my_list = ['apple', 'banana', 'orange']
random_element = random.choice(my_list)
print(random_element)

以上是我们日常生活中最常用的10个算法。它们涉及了排序、变换、路径搜索、加密、哈希、压缩、控制以及随机数生成等多个领域，并在各自的应用场景中发挥着重要作用。深入理解这些算法可以帮助我们更好地理解和应用现代技术。

总结：

这些算法在计算机科学和信息技术领域扮演着重要的角色，它们为我们提供了强大的工具来解决各种问题。无论是搜索引擎的排名、数据加密的安全性，还是自动化控制系统的稳定性，这些算法都为我们的现代世界带来了巨大的影响。通过学习和应用这些算法，我们能够更好地理解和改善我们周围的技术环境。