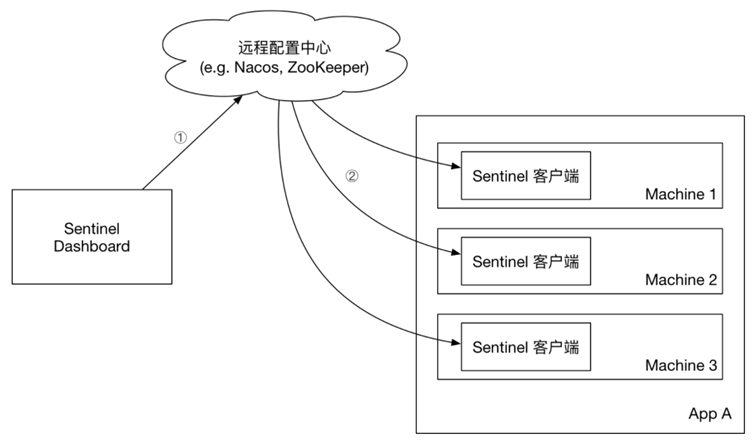
参数为 λ 的泊松过程的点间间距是相互独立的随机变量，且服从均值为 1/λ 的 指数 分布。

病人以每小时3人的泊松流到达医院，设该医院只有一个医生服务且容量为无穷，医生服务的时间服从指数分布，并且平均服务一个病人为30分钟，则当 t → ∞ 时，医生空闲的比例为9，平均有平均有 ∞ 个病人在等待看医生，病人的平均等待时间为 ∞ ，一个病人等待超过
一个小时的概率为 1 ，在医生服务1个病人的时间内平均有1.5个病人到达医院。

设某保险公司收到的索赔遵循一个参数为 λ的泊松过程{N(t), t ≥ 0}，假设一个索赔是车险的概率为p，以X(t)表示时间(0,t]内保险公司收到的车险索赔的次数。证明{X(t),t>0}是参数为ρλ 的泊松过程。

设齐次马氏链{X(n),n=0,1,2,…}的状态空间E={0,1,2,3}，一步状态转移矩阵：

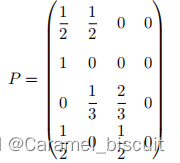
1. 画出状态转移图
2. 讨论各状态性质
3. 分解状态空间

设齐次马氏链 {X(n), n = 0, 1, 2, . . . } 的状态空间 E = {1, 2, 3}，一步状态转移矩阵

某高速公路旁有一个加油站，汽车按平均每分钟5辆的泊松过程通过该加油站。假设通过该加油站的汽车有40%的来加油站加油，求

1. 在头2分钟和第3至第5分钟这两个时间区间内各有2辆汽车通过该加油站的概率。
2. 在头2分钟内，通过该加油站5辆汽车且仅有1辆汽车来加油站加油的概率。

某打字室有2个打字员独立打字，每个打字员打一份文稿的时间服从指数分布，平均20分钟，又假定文稿以泊松流到达，平均每小时到达5份，求系统到达平稳时

假设某电影网站有3台服务器，其中2台备用，只有一个维修工人。如果服务器正常工作时间服从指数分布，平均2天，而维修调整一台服务器的时间服从负指数分布，平均1天。求网站正常运转的概率及由于停机网站无法运行的概率。

某计算中心的信息交换站接受到的信息流为泊松流。每秒钟到达15份信息，信息从交换站输出服从指数分布，平均每秒钟20份，试求：若缓冲器的存储空间仅可存储4份信息，则平稳时的概率分布，信息损失的概率，信息交换站的平均信息数，缓冲器中的平均信息数，每份信息在交换站的平均逗留时间和平均等待时间。

M/M/c/K混合制排队系统，有c个服务台，K个座位，c<=K。当有K个位置已被顾客占用时，新到的顾客就自动离开，当系统中有空位置时，新到的顾客就进入系统排队等待服务。

设有一排队系统：顾客按参数为2的泊松流到达：顾客所需的服务时间序列独立、服从参数为5的2阶爱尔朗分布；系统只有一个服务台，容量为无穷大；顾客到达时，若服务台空闲就立即接受服务，否则就排队等待，并按先到先服务的顺序接受服务，而且到达过程与服务过程彼此独立。试求该系统的平均队长、平均等待队长、平均等待时间、平均逗留时间。

M/G/1/ ∞ 排队系统

对于一般服务或一般到达的排队系统，并不是任何时刻系统都具有马尔可夫性，只是在某些特殊的随机时刻系统才具有这种性质，我们称这种随机时刻为再生点，即从这个时刻起，系统好像又重新开始一样。利用再生点，一般服务或一般到达的排队系统可化成马尔可夫链。次这种方法叫做嵌入式马尔可夫链法，次方法的精髓是找再生点。

设有2台复印机，平均复印文件的速度为8件/分钟，文件到达率为12件/分钟，假设每件文件固定页数，试求：

M/M/c/m/m系统

c个工人共同看管m台机器，机器运转时会发生故障而停止生产，这时需要工人进行适当的维修，修复后立即投入运转。

某单位有10辆汽车，3个修理工，假定每辆车平均30天修理一次，平均修理时间为6天，汽车正常运行时间和修理时间都服从指数分布

某计算中心的信息交换站接收到的信息流为泊松流，每秒到达15份信息，信息从交换站输出服从指数分布，平均每秒钟20份，若存储空间仅可存储4份信息，试求

M/M/c/K

混合制排队系统，系统中有K个位置，c个服务台独立并行服务，c≤K。当K个位置已被顾客占用时，新到的顾客就自动离开，当系统中有空位置时，新到的顾客就进入系统排队等待服务。

一台计算机有2个终端，假定存储空间无限，每个终端计算一个题目的时间服从指数分布，平均30分钟；题目到达是平均每小时5个的泊松过程。则t->无穷时，计算机空闲的概率

设电话总机在[0,t)内接到电话呼叫次数N(t)是平均每分钟2次的泊松过程，

• 2分钟内接到2次呼叫的概率。
• 第1分钟和第2分钟内各接到1次呼叫的概率。

袋中有黑白两色的球各10个，每次从袋中随机取出一个球后，放进一个不同色的球。令X(n)为取了n次后袋中的白球数。证明{X(n),n=1,2,3}为正常返不可约齐次马尔科夫链。

设电话总机有4条线路，呼叫按泊松流到达，平均每10分钟1.5次，通话时间服从指数分布，平均20分钟。试求：

**某系统利用2台计算机进行容错处理。如果1台计算机正常工作时间服从负指数分布，平均10天，而计算机损坏时由1名工程师维修，维修一台计算机的时间服从负指数分布，平均5天。求：2台计算机都正常运行的概率和由于计算机损坏无法运行的概率，系统中平均运行的计算机数。
**

某单位需要购置计算机，有两种方案：一种是购置1台大型计算机，一种是购置2台小型计算机，每台小型计算机是大型计算机处理能力的1/2，上机的题目以泊松流到达，平均5分钟9个，而使用大型计算机计算题目的时间服从指数分布，平均每分钟4个。试从平均等待时间的计算，来分析哪种方案合适

进入商店的顾客数是数学期望为100的随机变量，顾客所花的钱是数学期望50元的相互独立的随机变量。

设N（t）表示发射源在[0,t)内发射的粒子数，{N(t),t>=0}是平均率为

在传送数字0和1的通讯系统中，每一传送数字必须经过若干级。第i级正确传送的概率为pi，X(0)表示进入该系统第一级的数字，X(n)表示离开通讯系统第n级的数字。{X(n),n=0,1,2,…}是状态空间E={0,1}的齐次马氏链。若更设pi=p

设有6个球（其中2个红球4个白球）分别放于甲、乙两个盒子中，每盒3个。令每次从两个盒子中各取一个球进行交换，X(0)表示开始时甲盒中红球的个数，X(n)表示经过n次交换后甲盒中的红球数。

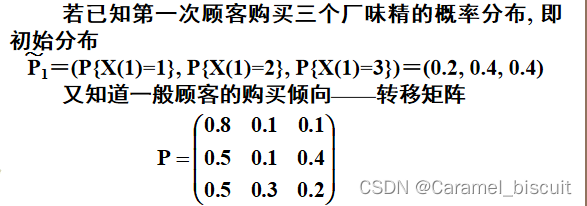
若顾客的购买是无记忆的，即已知顾客现在的购买情况，顾客将来购买的情况不受过去历史购买的影响，而只与现在的购买情况有关。现在市场上供应A、B、C三个不同厂生产的50g袋装味精。X(n)=1、X(n)=2、X(n)=3分别表示顾客第n次购买A、B、C厂的味精。若已知第一次顾客购买三个厂味精的概率分布，即初始分布，又知道顾客的购买倾向——转移矩阵。

A、B、C三家公司决定在某一时间推销一种新产品，当时它们各拥有1/3的市场，然而一年后，情况发生了如下的变化：

设有2个通信通道，每个通道正常工作时间服从参数为

设顾客到达为泊松流，平均每小时到达个顾客。一个顾客在系统内逗留每小时损失c1元，服务机构的费用正比于服务率u，每小时每位顾客的费用c2

某售票点有两个售票口，顾客以8人/分钟的泊松流到达，每个窗口的售票时间服从参数为5人/分钟的负指数分布，试比较以下两种排队方案的运行标准：

1. 顾客到达以后，以1/2的概率站成两个队列
2. 顾客到达后排成一个队列，发现哪个窗口空闲，就接受该窗口的服务。

设有一个信息交换中心，信息流为泊松流，每分钟到达240份，线路输出率为每秒800个字符，信息长度近似负指数分布，平均长度176个字符。要使在任何瞬间缓冲器充满的概率不超过0.005，问缓冲器的容量K至少应取多大？

设某计算机有4个终端，用户按泊松流到达，平均每10分钟到达1.5个用户。假定每个用户平均用机时间为20分钟，用机时间服从负指数分布，如果4个终端被占用，用户到其他计算机处接受服务。

某航空公司要保证正常的运营，应保证有12台发动机处于良好状态的概率不低于0.995，设每台发动机正常运转时间服从负指数分布，平均连续运转时间为3个月，有2个维修工负责其修理工作，修理时间也服从负指数分布，平均修复时间为5天，问：在满足要求的前提下，应该备用多少台发动机？