目录

目录

一、二叉树的创建与遍历

1.创建二叉树

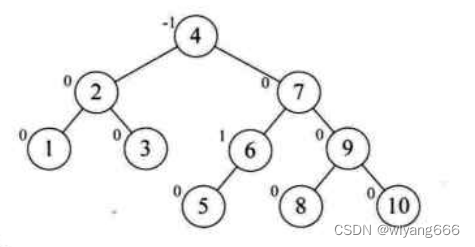
构建出来的树如图：

2.二叉树的销毁

3.二叉树的前序遍历[Leetcode144.力扣]

4.二叉树的中序遍历

5.二叉树的后序遍历

二、二叉树的实现

1.获取树中节点的个数

2.获取叶子节点的个数

3.获取第K层节点的个数

4.获取二叉树的高度[Leetcode104.]

5.判断是否为单值二叉树[leetcode965.]

6.检查两棵树是否相同[Leetcode100.]

7.判断是否为另一棵树的子树[Leetcode572.]

8.查找二叉树中值为x的节点

9.翻转二叉树[Leetcode226.]

10.对称二叉树[Leetcode101.]

11.二叉树的遍历[Nowcoder KY11.]

12.判断一棵二叉树是否为平衡二叉树[Leetcode110.]

13.二叉树的层序遍历

14.判断一棵树是否为完全二叉树

总结

---

一、二叉树的创建与遍历

1.创建二叉树

        从0创建一棵二叉树，首先需要定义树的节点结构，定义之后需要在内存中开辟空间，初始化节点，然后链接节点中的左右指针

typedef int TreeNodeDataType;

typedef struct TreeNode{
    TreeNodeDataType data;
    struct TreeNode * left;
    struct TreeNode * right;
}TDNode;

//在内存中开辟一个树的节点
TDNode * BuyTDNode(TreeNodeDataType x)
{
    TDNode * node = (TDNode *)malloc(sizeof(TDNode*));
    if(node == NULL)
        return;
    //创建好之后初始化
    node->data = x;
    node->left = NULL;
    node->right = NULL;
//创建一棵树
int main()
{
    TDNode* n1 = BuyTDNode(1);
	TDNode* n2 = BuyTDNode(2);
	TDNode* n3 = BuyTDNode(3);
	TDNode* n4 = BuyTDNode(4);
	TDNode* n5 = BuyTDNode(5);
	TDNode* n6 = BuyTDNode(6);


    n1->left = n2;
	n1->right = n4;
	n2->left = n3;
	n4->left = n5;
	n4->right = n6;
}

构建出来的树如图：

2.二叉树的销毁

        由于二叉树中的节点是动态开辟出来的内存空间，所以在不使用的时候需要动态销毁。

void DestoryTree(BTNode * root)
{
    free(root->left);
    free(root->right);
    root->val = 0;
    free(root);
}

//注意这里虽然free掉了root,但是这里只是形参，最后在主函数中应该把这个节点置空

 

3.二叉树的前序遍历[Leetcode144.力扣]

        给一棵树的根节点root,返回它节点值的前序遍历，前序遍历的顺序是：根节点-左孩子-右孩子，可以使用递归的方法，把每个子树都看成由左右孩子组成，访问根节点0，然后访问左节点1，此时把左节点1当作根节点0，若还有左节点1，继续访问，访问右节点2，返回到上一层的左节点1，再访问上一层的右节点，直到遍历完整棵树

//按照前序打印这棵树 
void PreOrder(struct TreeNode * root)
{
    if(root ==NULL)
        return;
    printf("%d ",root->data);
    PreOrder(root->left);
    PreOrder(root->right);
}

//打印结果： 1 2 3 4 5 6 

力扣 题解，首先这道题核心也是二叉树的前序遍历，但是要返回遍历的结果，Note中注释返回的结果需要自己开空间，即自己定义一个数组存放遍历的数，题中形参只给了根节点，和一个int * 类型(指针）的returnSize,这里的returnSize是返回的数组大小。

解题逻辑：首先判断树是否为空树，如果是空树return；如果不是空树则开始前序遍历，前序的顺序是根节点，左子树，右子树，所以可以使用递归的方法。首先动态开辟一个数组，  数组中存放遍历的结果,每遍历一个，数组的下标+1,即returnSize+1,如果遍历到空节点，返回上一层递归，再去递归它的左子树，右子树。

Traversal(struct TreeNode * root,int *returnNum,int *returnSize)
{
    //调用的人需要数组和数组的大小，1.可以返回结构体，2.返回指针
    //如果returnSize为int类型，当前的形参只是实参的临时拷贝，不改变实参
    //所以使用一个int * ，当解引用使用形参的时候，会改变实参。
    if(root ==NULL)
        return;
    returnNum[(*returnSize)++] = root->val;
    Traversal(root->left,returnNum,returnSize);
    Traversal(root->right,returnNum,returnSize);
}

int * preorderTraversal(struct TreeNode * root, int * returnSize)
{
    //先自己开辟要返回的数组  数组的类型为int 型，要返回int *类型，所以使用一个指针指向数组
    int * returnNum = (int *)malloc(sizeof(int *)*100);
    //returnSize 为返回的数组的大小 
    *returnSize = 0; // 初始化为0
    if(root ==NULL)
        return NULL;
    //前序遍历单独写一个函数
    Traversal(root,returnNum,returnSize);
    return returnNum;

看完别人的思路，感觉如下的方式写更优解，上面开辟的数组大小是固定的，可以写一个函数统计这棵树的节点个数，再去开辟。

int * preorderTraversal(struct TreeNode * root, int * returnSize)

4.二叉树的中序遍历

void Inorder(struct TreeNode * root)
{
    if(root == NULL)
        return;
    Inorder(root->left);
    printf("%d",root->data);
    Inorder(root->right);
}

5.二叉树的后序遍历

void PostOrder(struct TreeNode * root)
{
    if(root ==NULL)
        return;
    PostOrder(root->left);
    PostOrder(root->right);
    printf("%d",root->data);
}

二、二叉树的实现

1.获取树中节点的个数

使用分治思维，统计根节点的左右节点的个数。遇到左节点，再去统计它的左右节点个数，递归。

一种经典的错误写法如下：

int TreeSize(struct TreeNode * root)
{
    if(root ==NULL)
        return;
    int size = 0;
        size++;
    TreeSize(root->left)；
    TreeSize(root->right);
    return size;
}

这种写法错误的点在于，没有完全理解递归的栈帧。当定义size的时候，size是一个局部变量，返回的size并不是总共的size,统计出来的左右节点个数没有保存，也没有返回给上一层的根节点。

正确写法如下：使用一个三目运算符，如果节点为空，返回0，如果不为空，统计左右节点的个数，再加上自己，即所求的所有的节点个数。

int TreeSize(struct TreeNode * root)
{
    return root ==NULL ? 0:TreeSize(root->left)+TreeSize(root->right) + 1;
}

2.获取叶子节点的个数

获取叶子节点个数，先明白叶子节点的定义就是没有左右子树的节点，那么在函数中可以写如果根为空，返回0，如果节点不为空，统计左右子树节点的叶子节点，叶子节点即为(root->left==NULL && root->right==NULL)代码如下：

int TreeSizeLeaf(struct TreeNode * root)
{
    if(root ==NULL)
        return 0;
    if(root->left && root->right ==NULL)
        return 1; 
    return TreeSizeLeaf(root->left)+TreeSizeLeaf(root->right);
}

3.获取第K层节点的个数

如图所示：因为这个结构为一棵二叉树，认为节点1为第一层，第一层只会有一个节点。如果现在要求1的第三层的节点个数[3,5,6],无法直接访问到，但是对于2和4[3,5,6]分别是他们的左子树和右子树，对于2和4，[3,5,6]是他们的第二层。对于[3,5,6]本身，他们就是第一层，如果第一层不为空，就返回1，如果第一层为空，返回0。

1的第三层 == 2的第二层(1的左子树）+4的第二层（1的右子树）

                 == （3的第一层（2的左子树）+空 (2的右子树))+(5的第一层（4的左子树）+6的第一层（4的右子树))

由此类推 求当前的第K层节点个数 == 左子树的K-1层+右子树的K-1层，直到k ==1,当k==1的时候，判断这个节点是否为空，如果为空，返回0，如果不为空返回1

int TreeLeveSize(struct TreeNode * root,int k)
{
    if(root ==NULL)
        return 0;
    if(k==1)
    {
        //这里不用再写判断是否为空，因为在调用递归的时候，已经先判断了
       return 1;
    }
    return TreeLevelSize(root->left,k-1)+TreeLevelSize(root->right,k-1);
}

4.获取二叉树的高度[Leetcode104.]

思路：比较当前节点的左右子树的深度，哪个高，返回哪个。树的深度如果只有根节点，深度为0，如果有左子树或者有右子树，深度为1。比较两个数的深度的时候需要有两个统计变量，哪个大返回哪个值+1，+1的原因在于，如果为空，则有0层，如果有一个节点，本层就是1，返回到上一层就是2。

int TreeHeight(struct TreeNode * root)
{
    if(root ==NULL)
        return 0;
    int lh = TreeHeight(root->left);
    int rh = TreeHeighr(root->right);
    return lh > rh? lh+1:rh+1;
}

5.判断是否为单值二叉树[leetcode965.]

题目：如果二叉树的每个节点都具有相同的值，那么这个树就是单值二叉树。题目链接:力扣

思路：当前节点为根节点，判断它和左右子树的值是否相同，如果相同，继续判断，先走到左子树，判断它和它的左右子树是否相同，相同再判断原来根节点的右子树，依次递归。

思想是顺着这个顺序，写代码可以反着写，即我遇到了我的左子树或者右子树和我的值不相同，就return false，如果相同，就继续判断，直到遍历完这棵树。在这里要注意，左右子树可能为空，如果为空就无法访问到val，所以要加上这个条件。

bool isUnivalTree(struct TreeNode * root)
{
    if(root==NULL)
        return true;
    if(root->left && root->left->val != root->val)
        return false;
    if(root->right && root->right->val !=root->val)
        return false;
    //如果有1个为false，就返回false
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

6.检查两棵树是否相同[Leetcode100.]

题目：给两棵二叉树的根节点p,q，编写一个函数来判断两棵树是否相同（如果两棵树在结构上相同，并且节点具有相同的值，则认为他们相同） 题目链接：力扣

思路：先判断它们的根是否相同，如果根相同，比较左子树，左子树相同，再比较右子树。如果都相同，再比较子节点的左子树和右子树。思路顺着写，代码反着写。

bool isSameTree(struct TreeNode * p,struct TreeNode * q)
{
    if(p==NULL && q==NULL)
        return true;
    if(p==NULL || q==NULL)
        return false;
    if(p->val != q->val)
        return false;
    return isSameTree(p->left,q->left) &&isSameTree(p->right,q->right)
}

7.判断是否为另一棵树的子树[Leetcode572.]

题目：给两棵二叉树root,subroot。检验root中是否包含和subroot具有相同结构和节点值的子树，如果存在，返回true,如果不存在，返回false。题目链接:力扣

思路:可以借用判断两个树是否相同的函数

//判断两棵树是否相同
bool isSameTree(struct TreeNode * p,struct TreeNode * q)
{
    if(p == NULL && q ==NULL)
        return true;
    if(p == NULL || q == NULL)
        return false;
    if(p->val != q->val)
        return false;
   return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}



bool isSubtree(struct TreeNode * root, struct TreeNode * subRoot)
{
    if(root ==NULL)
        return;
    if(isSameTree(root,subRoot))
        return true;
    //在左右子树中寻找 有一个为true就返回true;
    return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

8.查找二叉树中值为x的节点

思路：先判断根，根的值 == x ，返回，如果不等于，再找到左子树，如果左子树的值相等返回，不相等去找右子树，找到返回，找不到返回null（找完了）

但是这里需要注意，如果在左子树中找到返回，返回之后给上一层，并没有返回给第一个函数的return,所以需要保存一个值，找到之后保存这个结果。

BTNode * Find(BTNode * root,int x)
 {
    if(root->data == x)
        return root;
   BTNode * ret1 =  Find(root->left,x)
      if(ret1)
         return ret1;
   BTNode * ret2 = Find(root->right,x)
      if(ret2)
         return ret2;
    return NULL;
}

9.翻转二叉树[Leetcode226.]

题目:给一棵二叉树的根节点root，翻转这棵树，并返回其根节点，题目链接:力扣

思路：给一个tmp交换，然后递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
struct TreeNode* invertTree(struct TreeNode* root){
    if(root ==NULL)
        return NULL;
    struct TreeNode * tmp = (struct TreeNode *)malloc(sizeof(struct TreeNode *));
    tmp = root->left;
    root->left = root->right;
    root->right = tmp;

    invertTree(root->left);
    invertTree(root->right);
    
    return root;

}

 

10.对称二叉树[Leetcode101.]

题目：给一个二叉树的根节点root,检查它是否轴对称。题目链接:力扣如图:

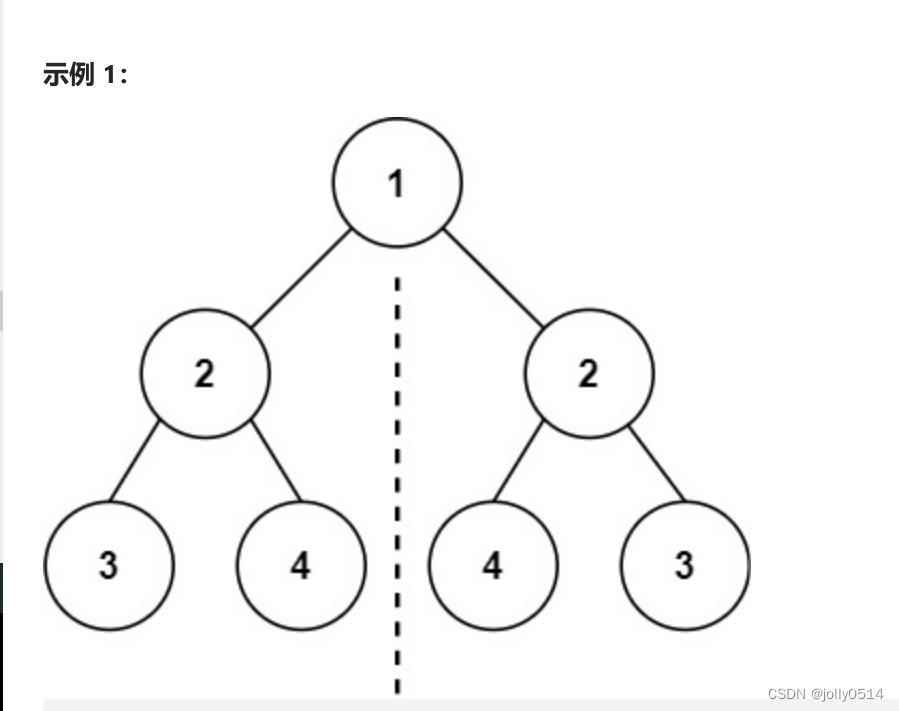
 思路:之前判断两个树是否相同，都是用左子树和左子树比较。这道题目可以使用递归的方法，比较左子树和右子树

bool _isSymmetric(struct TreeNode * p , struct TreeNode * q)
{
    if(p== NULL && q ==NULL)
        return true;
    if(p ==NULL || q==NULL)
        return false;
    if(p->val != q->val)
        retrun false;
    return _isSymmetric(p->left,q->right) && _isSymmetric(p->right,q->left);
}


bool isSymmetric(struct TreeNode * root)
{
    if(root == NULL)
        return false;
    return _isSymmetrict(root->left,root->right);
}

 

11.二叉树的遍历[Nowcoder KY11.]

题目:编写一个程序，读入用户输入的一串先序遍历的字符串，根据此字符串建立一个二值二叉树（以指针方式存储），例如：ABC##DE#G##F###,其中#表示的是空格，空格字符代表空树，建立起二叉树之后，再对二叉树进行中序遍历，输出遍历结果。

题目链接：二叉树遍历_牛客题霸_牛客网

题目思路:首先要重建这棵树，现在是以前序的遍历存储，根据前序再递归，分别存入到它的左右子树中。然后中序遍历输出

struct TreeNode 
{
    char val;
    struct TreeNode * left;
    struct TreeNode * right;
 }
struct TreeNode * rebulidTree(char * str,int *pi)
{
    if(str[*pi] == "#")
     {   (*pi)++;
         retrun NULL;
     }
    //构建节点，如果不为空，存入值，继续遍历它的左右子树 
    struct TreeNode * root = (struct TreeNode *)malloc(sizeof(struct TreeNode *));
    
    root->val = str[(*pi)++];
    root->left = rebuildTree(str,pi);
    root->right = rebuildTree(str,pi);
    return root;
}
//中序遍历
  void Inorder(struct TreeNode * root)
    {
        if(root ==NULL)
            return;
        Inorder(root->left);
        printf("%c",root->val)
        Inorder(root->right);
    }
int main()
{
    char str[100];
    scanf("%s",&str);
    int i = 0;
    //先重建这棵树
    struct TreeNode * root = rebuildTree(str,&i);
    Inorder(root);
    return 0;
}

12.判断一棵二叉树是否为平衡二叉树[Leetcode110.]

题目:给定一颗二叉树，判断它是否是高度平衡的二叉树，高度平衡：一个二叉树的每个节点的两个左右子树的高度绝对值不超过1，题目链接：力扣

思路：使用递归，统计它的左右子树，判断左右子树的高度，如果大于1，返回false,如果不大于1，继续遍历它的左右子树，直到root为空。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

int TreeHeight(struct TreeNode * root)
{
    if(root ==NULL)
        return 0;
        int leftHeight = TreeHeight(root->left);
        int rightHeight = TreeHeight(root->right);
        return leftHeight > rightHeight ? leftHeight+1 :rightHeight+1;
}

bool isBalanced(struct TreeNode* root){

    if(root ==NULL )
        return true;
    //统计左右子树的高度，左右子树高度的绝对值超过1返回false,否则返回true;
    int left_height = TreeHeight(root->left);
    int right_height = TreeHeight(root->right);
       
    if(abs(left_height -right_height) >1)
        return false;

        return isBalanced(root->left) && isBalanced(root->right);
    return true;

}

 

13.二叉树的层序遍历

        思路：二叉树的层序遍历就是先遍历根节点，然后遍历它的左右子树，遍历完后，再遍历左子树的左右子树，遍历右子树的左右子树。可以使用一个队列，当队列为空的时候，进入根节点，然后出根节点，进入它的左右子树，出根节点，进入左右子树。直到出到队列为空，结束遍历。

        队列之中，如果存二叉树的节点的值，会找不到左右孩子，如果存二叉树的节点，占用空间较多，可以存二叉树的节点指针。代码如下：

void LevelOrder(BTNode * root)
{
    Queue q;
    QueueInit(&q);
    if(root ==NULl)
        return;
    if(root)
        QueuePush(&q,root);
    while(!QueueEmpty(&q))
    {
        BTNode * front = QueueFront(&q);
        print(front->data);
        QueuePop(&q);
        if(front->left)
            QueuePush(&q,front->left);
        if(fornt->right)
            QueuePush(&q,front->right);
     }
}

14.判断一棵树是否为完全二叉树

同样，也是用层序遍历的方法，创建一个队列，如果出的节点是空，后面出的节点不是空，那就不是完全二叉树，如果出空之后后面仍是空，那就是完全二叉树

bool TreeComplete(BTNode * root)
{
    //创建队列
    Queue q;
    QueueInit(&q);
    if(root)
       QueuePush（&q,root);
    while(!QueueEmpty(&q))
    {
        BTNode * front = QueueFront(&q);
        QueuePop(&q)
        if(front ==NULL)
        {
            break;
        }
        
        else
        {
            QueuePush(&q,front->left);
            QueuePush(&q,front->right);
        }
    }
        //break出来判断后面的队列是否为空，如果为空，return true,如果不为空，return false;
        while(!QueueEmpty(&q)
        {
            front = QueuePop(&q);
            if(front != NULL)
                return false;
            Destroy(&q);
            return true;
        }
}

---

总结

二叉树的相关函数大多用的递归的方法，这个时候需要多画图，理解函数的栈帧，调试看bug。技术有限，如有错误请指正。