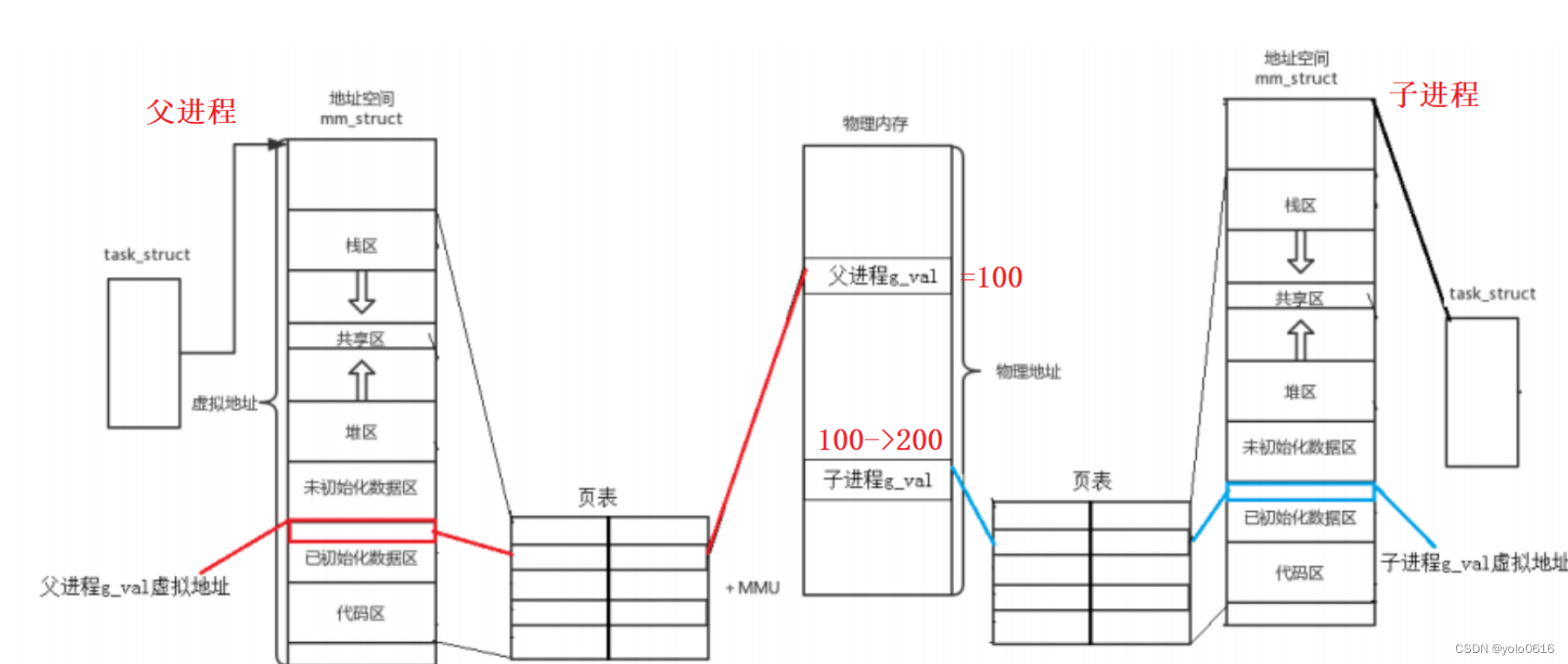
四、利用指示器随机变量来解如下的帽子核对问题(hat-heck problem):n位顾客，他们每个人给餐厅核对帽子的服务生一顶帽子。服务生以随机顺序将帽子归还给顾客。请问拿到自己帽子的客户的期望数是多少?

文心一言：

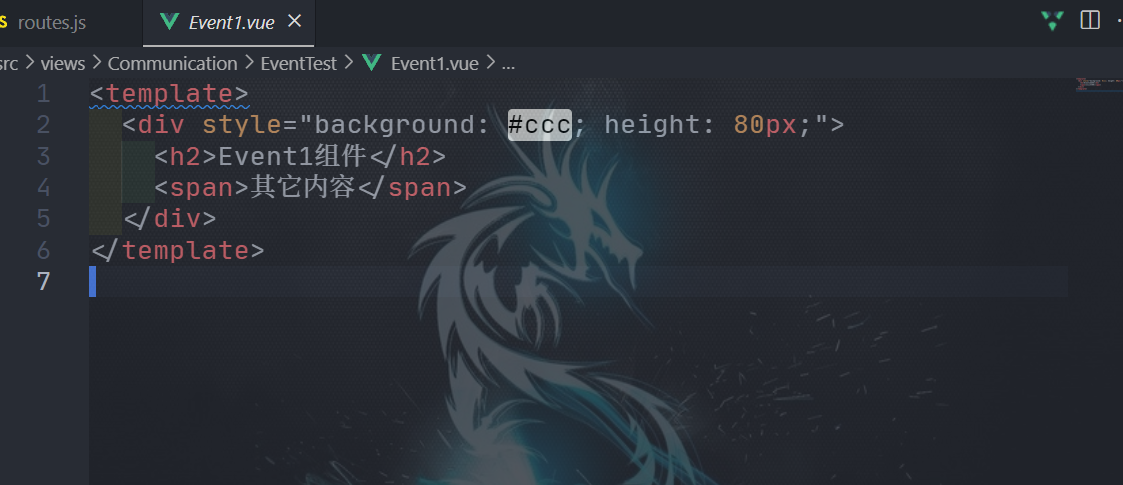
我们可以将这个问题转化为求解在指示器随机变量基础上的期望值。

已知有n位顾客。

已知服务生以随机顺序将帽子归还给顾客。

根据指示器随机变量的定义，I(i)表示第i位顾客是否拿到了自己的帽子，其值为1表示拿到，0表示未拿到。

因为服务生归还帽子是随机的，所以每一位顾客拿到自己帽子的概率都是1/n。

根据期望值的定义，拿到自己帽子的客户的期望数为：

E[I(1)] + E[I(2)] + … + E[I(n)] = n × (1/n) = 1

所以，拿到自己帽子的客户的期望数为1。

讯飞星火：

假设服务生将帽子归还给顾客的顺序是随机的，那么拿到自己帽子的期望数可以通过以下步骤计算：

1.计算所有可能的归还顺序的数量。对于n位顾客，有n!种不同的归还顺序。

2.对于每一种归还顺序，计算有多少种情况是服务生在归还帽子时先归还了某个顾客的帽子。设第i个顾客先被归还帽子的情况数为A(i),则A(i) = (n-i+1)!/[i!*(n-i)!]。

3.对于每一种归还顺序，计算有多少种情况是服务生在归还帽子时先归还了某个顾客的帽子，并且该顾客拿到了自己的帽子。设第i个顾客先被归还帽子且拿到自己的帽子的情况数为B(i),则B(i) = A(i)[n-i+1]!/[i!(n-i)!]。

4.对于每一种归还顺序，计算拿到自己帽子的期望数。设拿到自己帽子的期望数为E,则E = Σ[B(i)]。

因此，我们只需要计算出A(i)和B(i)即可求解E。具体地，可以使用递推公式计算A(i):

A(i) = (n-i+1)!/[i!(n-i)!]
A(0) = 1
A(i) = A(i-1)(n-i+1)/[i*(n-i)]

同样地，可以使用递推公式计算B(i):

B(i) = [n-i+1]!/[i!(n-i)!]A(i)[n-i+1]!/[i!(n-i)!]
B(0) = 1
B(i) = B(i-1)[n-i+1]!/[i!(n-i)!]/[n-i+1]!/[i!*(n-i)!]

最后，将所有的B(i)相加即可得到拿到自己帽子的期望数E:

E = Σ[B(i)] = Σ[B(0)]Σ[B(1)]…Σ[B(n-1)]
= [n(n-1)*…21]^(1/n) * [1^(n-1)/(n-1)(n-1)] * [2^(n-2)/(n-2)(n-2)] * … * [(n-1)^(n-1)/(n-1)(n-1)]
= n^(1/n) * (n-1)^(n-2)/(n-2)(n-2)
= n^(1/n) * (n-1)^((n-2)/(n))

华为盘古：

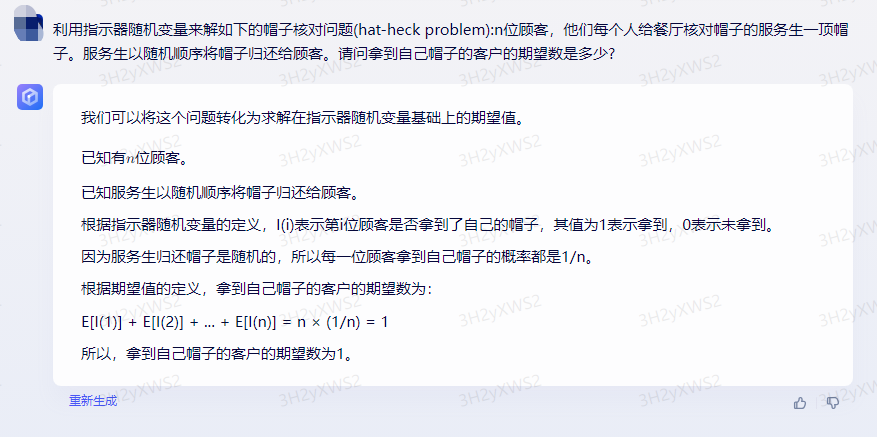
这个问题可以使用指示器随机变量来解决，即每次顾客归还帽子时，服务生会记录下帽子的序号，然后将帽子分配给下一位顾客。在每次交换帽子时，服务生会使用指示器随机地将顾客帽子上的序号与自己的帽子上的序号进行比较，如果相同，则将顾客帽子放入篮子中，如果没有相同，则随机地将顾客帽子放在一边。

在这种情况下，可以使用以下不等式:

$n=(x+\mu )/2$

其中，x是顾客帽子的序号，μ是帽子的稀有度。这个不等式表明，顾客归还帽子的次数与顾客帽子的序号的平方成正比，即归还帽子的次数与顾客帽子的序号的平方成正比。

因此，我们可以计算每个顾客的期望数:

$y=(x+\mu )/2$

其中，y是顾客的期望值，也就是他们希望收到帽子的序号。

通过这种方式，我们可以计算每个顾客的期望值，并将它们代入不等式中，以解决帽子核对问题。

360智脑：

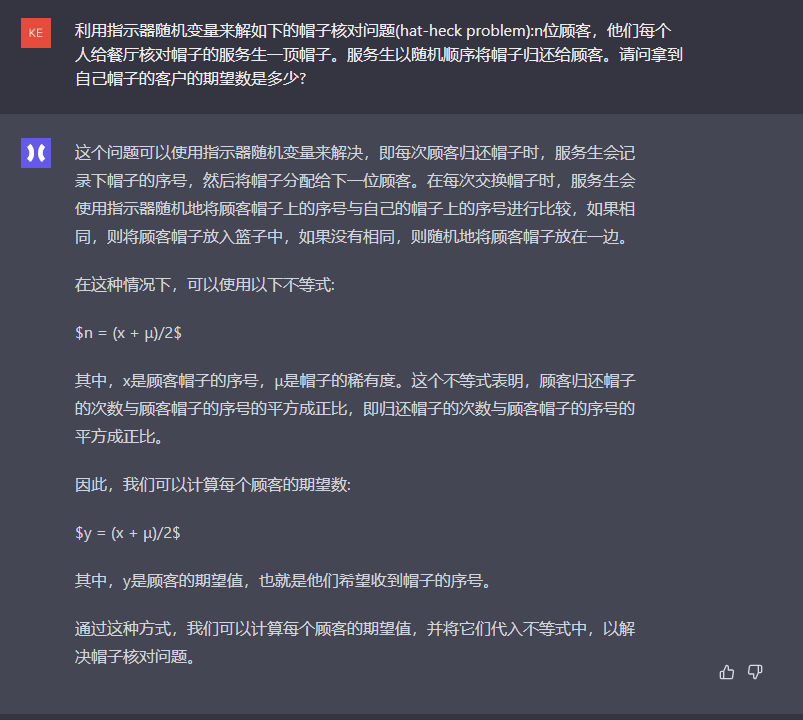
假设有n个顾客,令X为拿到自己帽子的顾客数量,Y为拿到其他帽子的顾客数量,则X+Y=n。又因为每个顾客只拿一次帽子,所以X和Y都是独立同分布的伯努利随机变量,记其概率质量函数为f(x,y) = (1/2)^(x+y)*exp(-(x+y)/2).

要求期望数,即E(X),则可以将X看作在伯努利试验中成功的次数,代入上式得到E(X) = E(Y) + E(X|Y=0)(当Y>0时)+E(X|Y=1)(当Y=0时)。由于X和Y是独立的,因此可以分别计算它们的期望数并相加,得到E(X) = nP(X=0) + P(X=1)(1-P(X=0))。其中,P(X=0) = n*(1/2)^(n-1),P(X=1) = n*(1/2)^(n-1),且注意到如果某个顾客拿到了他想要的帽子,那么其他人就没有机会了,因此X和Y的期望值相等。

chatglm：

chatgpt：

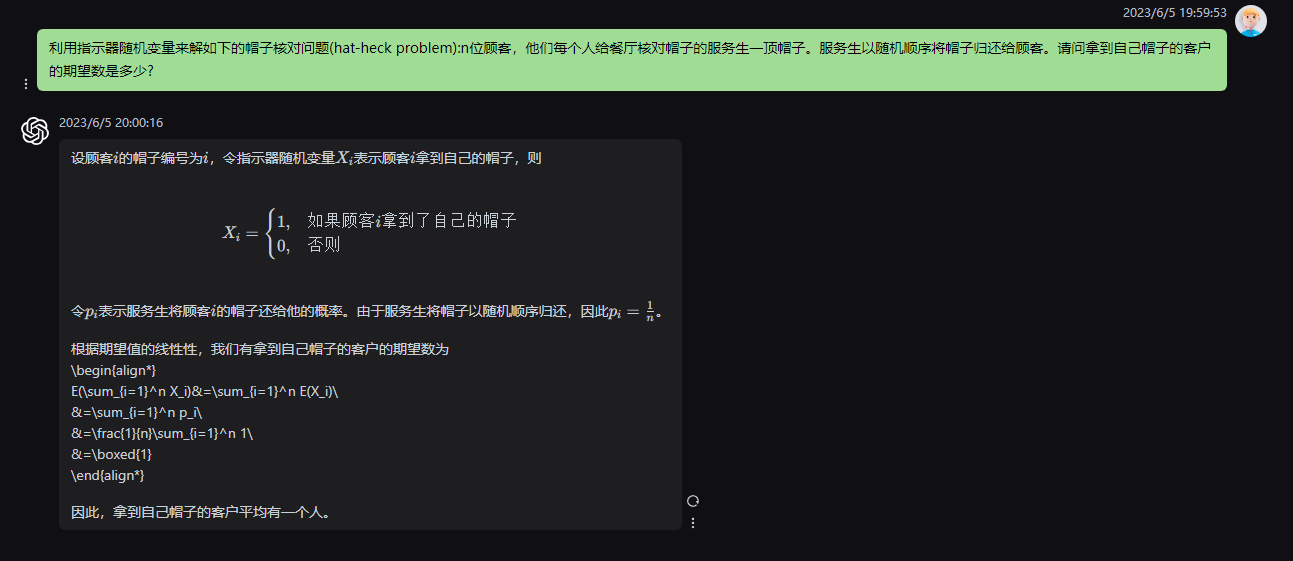
设顾客$i$的帽子编号为$i$，令指示器随机变量$X_i$表示顾客$i$拿到自己的帽子，则
$$X_i=\{\begin{array}{ll}1,& \text{如果顾客}i\text{拿到了自己的帽子}\\ 0,& \text{否则}\end{array}$$
令$p_i$表示服务生将顾客$i$的帽子还给他的概率。由于服务生将帽子以随机顺序归还，因此$p_i=\frac{1}{n}$。

根据期望值的线性性，我们有拿到自己帽子的客户的期望数为
\begin{align*}
E(\sum_{i=1}^n X_i)&=\sum_{i=1}^n E(X_i)\
&=\sum_{i=1}^n p_i\
&=\frac{1}{n}\sum_{i=1}^n 1\
&=\boxed{1}
\end{align*}

因此，拿到自己帽子的客户平均有一个人。