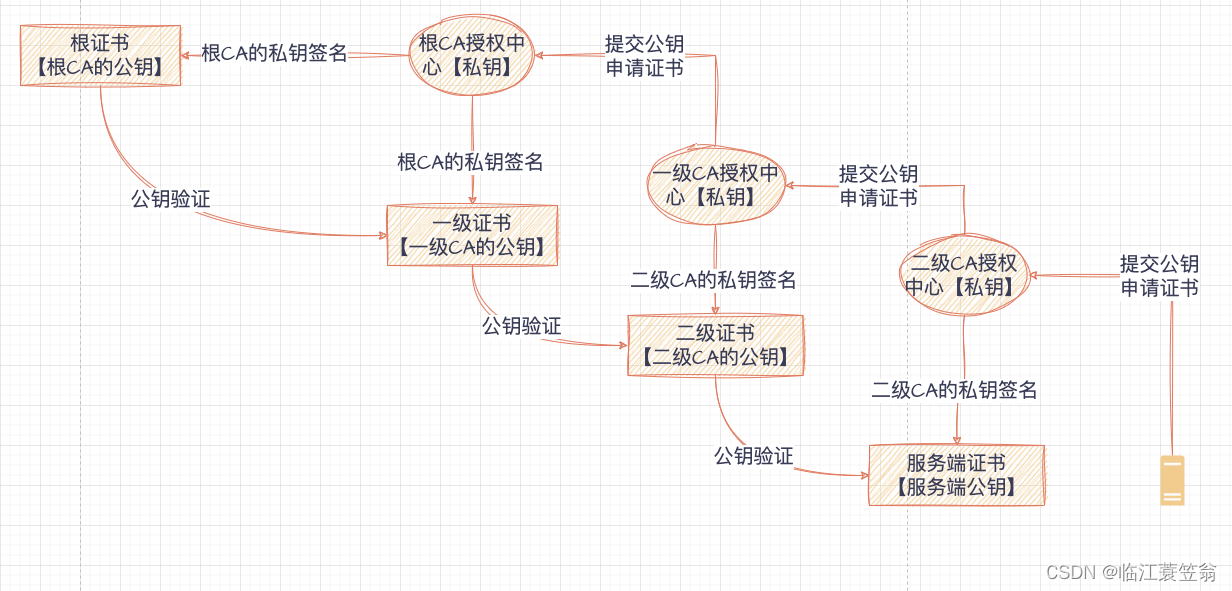
剑指 Offer 62. 圆圈中最后剩下的数字

leetcode

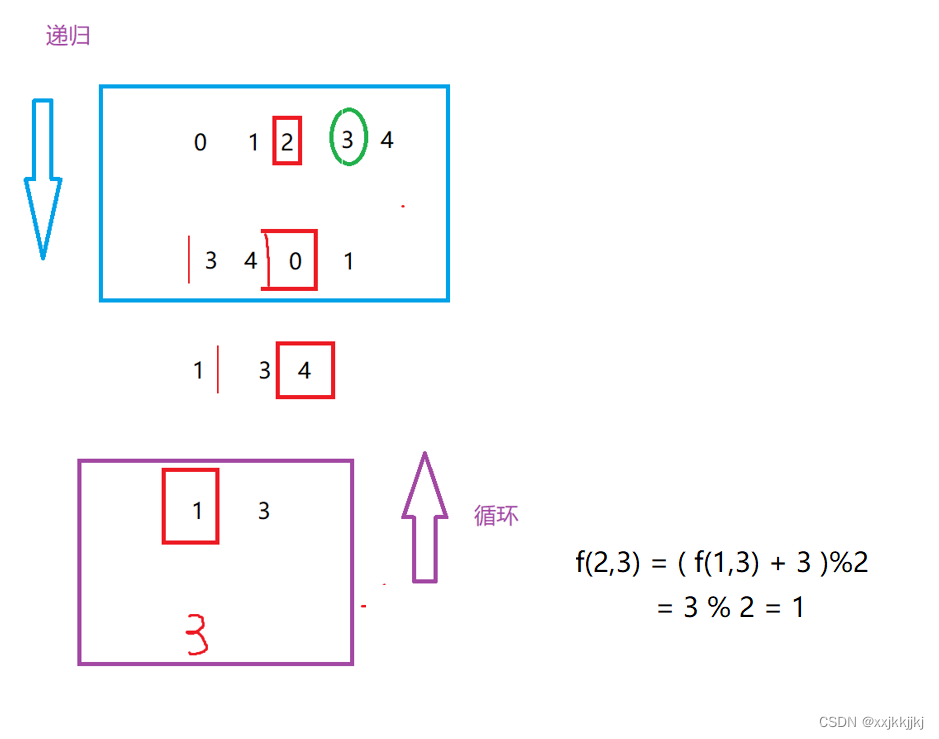
这题让我对递归和迭代又有了新的一层认识，首先一定要把图画对，就是模拟约瑟夫的这个过程
红色是被淘汰的位置，绿色的3是最后会活下来的人的位置
0 ~ n 正好是数组中的下标
重点在于计算 不同n时 幸存位置的下标，这里n = 5 去模拟淘汰的过程，2被淘汰，3就变成新的0号位置，循环下去模拟直到最后活下来的只有一个人就是3
n是固定的 那活下来的人也是固定的
本质就是我知道 n -1 = 4 时 队列情况是 3 4 0 1 时 3 的位置是0
（0 + 3）% 5 就可以得出 n = 5时 存活位置的下标 = 3
循环和递归就是 起点不同，分别是是开头（最下面）和结尾（最上面）

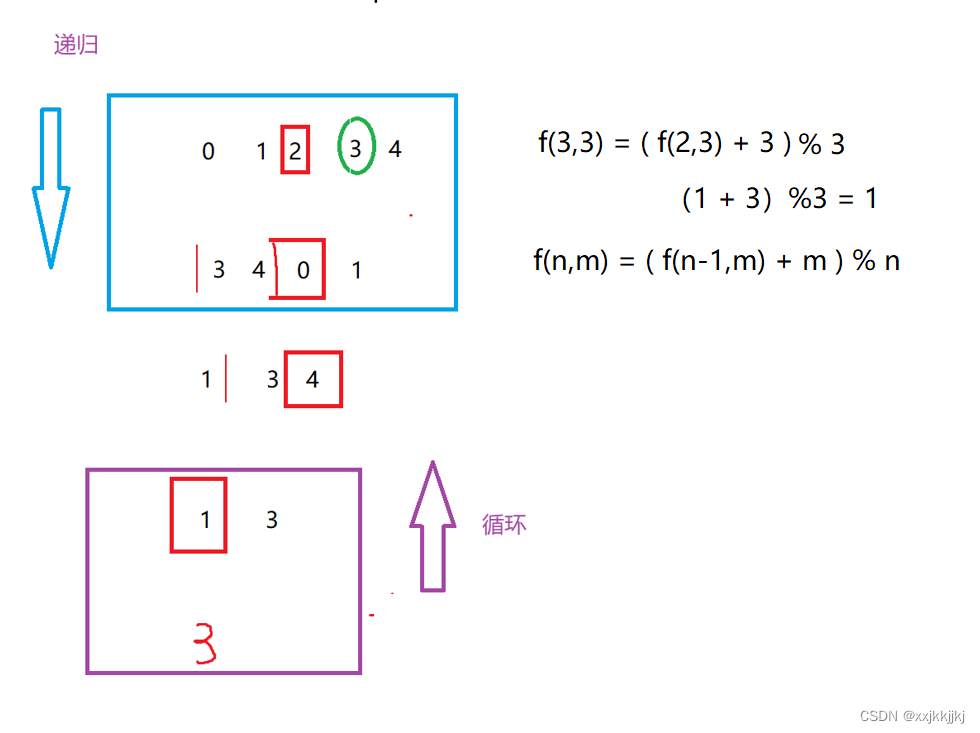
递归是从上往下，要知道当前f(n,m)的值， 需要知道 f(n-1,m)的值
那就出来了，求n 按照这个规律递归去求n-1
结束条件就是 n == 1 就是 0位置幸存

 int lastRemaining(int n, int m) {

        //递归  从上往下
         if(n == 1)
             return 0;
         return (lastRemaining(n-1,m)+m)%(n);

    }

循环是从下往上，只有一个人幸存位置就是0，那么从2个人开始，也就是n =2
这个好像更简单高效，毕竟循环不会栈溢出
根据画图和规律就是 ： pos = (pos + m) % i; // %取余控制pos不会越界而是在范围里走

int lastRemaining(int n, int m) {

        //递归  从上往下
        // if(n == 1)
        //     return 0;
        // return (lastRemaining(n-1,m)+m)%(n);

        //非递归 从下往上
        int pos = 0;
        for(int i = 2; i <= n; i++)
        {
            pos = (pos + m) % i; // %取余控制pos不会越界而是在范围里走
        }
        return pos;
    }