基于图像处理的圆检测与深度学习
- 摘 要
- 一、 绪论
- 二 、图像预处理
- 2.1 滤波算法
- 2.2 边缘检测
- 三 、圆识别与定位算法
- 3.2 定位算法
- 3.2.1 迭代算法
- 4.1 数据处理
- 五、深度学习介绍:
- 参考文献
摘 要
本文主要论述在图像处理的的基础上,为了克服图像背景中的亮度噪声、背景复杂和一些角度问题,通过图像预处理之后,利用边缘检测算法从而实现对图像边缘的识别,再利用利用牛顿迭代法,通过不断地迭代,与目标值进行迭代,从而达到实现检测圆的目标,以及圆心所在的位置。并对深度学习进行简单介绍,为后续学习做好准备。
关键词:图像处理;边缘检测;牛顿迭代;深度学习;
一、 绪论
随着中国制造业的快速发展,纺织业也在快速发展,但是如何去识别纱架上的纱筒是否还有余纱?因此就需在现实生产中利用工业摄像头去识别空桶。但是在识别的过程中往往会伴随着较多的噪声的产生,它的存在不仅影响着摄像头识别图片的精度和质量,进而可能造成生产事故。为了解决图片的噪声问题,基于视觉的机器人去噪声越来越广泛地应用[1],其中对采集的工件图像进行边缘检 测是其中一个非常重要的环节。 复杂的工业环境下图像采集、传输过程会产生的不同噪声,并且摄像头在不同的拍摄角度也会导致图片识别出现问题,形成椭圆等等,而且由于一天中的亮度是会变化的,因此我们设置的阈值也会受到影响,应该需要提高图片的边缘检测,现有的边缘检测技术难以同时减小两者对边缘检测的影响。传统的边缘检测方法常用的是二阶微分边缘检测算子,如 Laplace 算子、 Canny 算子和sobel 算子等[2-5]。二阶微分算子一般有定位精确,检测效率高的优点,然而二阶微分算子普遍对噪声比较敏感。
二 、图像预处理
2.1 滤波算法
目前存在的滤波法有许多,但是空间滤波根据其功能划分为平滑滤波和锐化滤波。平滑滤波:能减弱或者消除图像中高频率分量,但不影响低频率分量,在实际应用中可用来消除噪声。
目前使用比较普遍的有平均滤波、中值滤波与加权滤波等等。在该论文中我打算使用加权平均滤波,该滤波方法比平均滤波效果更好。我们使用如下图所示的3*3的平滑滤波器。
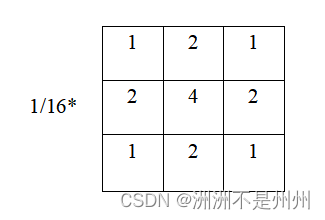
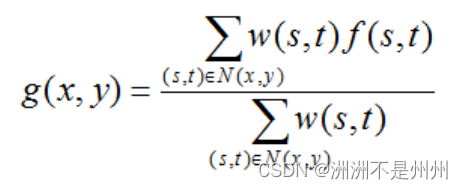
图一:平均滤波的计算公式
通过该3*3的滤波模板与原图像进行卷以后,可以滤除图片中一些常见的噪声。例如下图:

图二:未处理的原图

图三:处理后的图像
但是经过平滑滤波以后也会对图像的特征进行削弱,从而会造成对图像边缘模糊,从而为了去除这种影响,接下来应用了锐化滤波:与平滑滤波相反,能减弱或者消除图像中低频率分量,但不影响高频率分量,可使图像反差增加,边缘明显。实际应用可用于增强被模糊的细节或者目标的边缘。在这里我们打算使用拉普拉斯算子去进行锐化。
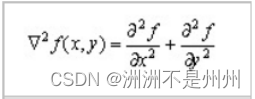
图四:拉普拉斯算子定义

图五:离散的掩膜表达方式
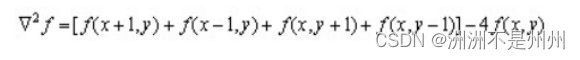
图六:数字化图片处理中的离散表达式
从上述中可以看出我们分别以f(x,y)以滤波中心,x轴的滤波表达式如下图所示:
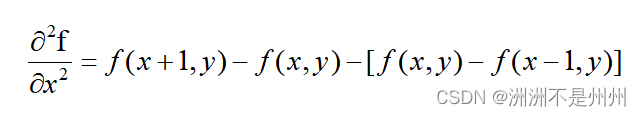

图七:拉普拉斯滤波的掩膜模板
通过对图像像素进行二次求导,从而能得到较好的图像边缘变化的特征。但是由于拉普拉斯算子对噪声的影响非常敏感,所以再使用拉普拉斯算子之前我们得先进行噪声滤波。下图将显示通过拉普拉斯滤波后图像边缘被显示的图片边缘。

图八:进行锐化后的图像
从过一些列的滤波后,噪声的干扰已经大部分解决了。接下来就研究边缘检测了。
2.2 边缘检测
目前有较多的边缘检车算法,例如:Laplace 算子、 Canny 算子和sobel算子等等。由于计算机计算能力的日益强大,所以较好的解决了canny算法计算量大的问题[6],并且canny算法提取出的边缘质量较高,在canny算法中关于连续性、细度和笔直度等线的质量也很出众,因此在该文章中我们优先优先选用canny边缘检测算法。Canny算法的核心是找出中心像素周围的8领域中,以灰度值最大的点为边界,再利用滞后阈值法进行计算。若小于则舍去,大于就保存。但是如上图所以我们发现图像的轮廓很细,这样不利于我们进行图像轮廓的检测,我们可以可以进行图像的膨胀。下式是膨胀的计算公式
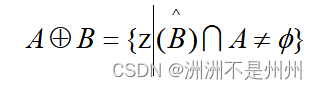
图九:膨胀公式
当我们的结构元素B越大时,此时发现通过膨胀后的轮廓变得更加清晰。我们会发现这是一个好的现象,为下一步进行边缘检测做好了准备。

图九:膨胀后的图像
从上图中我们可以看出录像中的轮廓在通过膨胀以后,轮廓变得清晰了许多,这也就表示着图像的大部分处理已经完成。接下我们将实现识别圆。
三 、圆识别与定位算法
3.1:识别圆算法
圆检测技术目前用处还是特别的广泛,例如我们在空桶检测中要用摄像机去检测圆中心,进而测试出我们需要的信息。对于一个圆,就需要用三个参数来确定。使用Hough梯度法的依据是圆心一定出现在圆上的每个点的模向量上,圆上点的模向量的交点就是圆心的所在位置。Hough梯度法的第一步就是找到这些圆心,这样三维的累加平面就转化为二维累加平面。第二步就是根据所有候选中心的边缘非零像素对其的支持程度来确定半径。在做 Hough 变换之前,需要对连续的图像做离散化处理,通过对半径步长的设定和图像中边缘点的存在情况,来对各种( a1,a2,r) 的组合进行投票。检测距离为 r的所有的像素点7 ,如果( a1,a2 )点的像素值大于 0,则将对应空间( a1,a2, r) 的数值加 1。然后通过设定一定的阈值,对最终的结果进行筛选,保留大于阈值的圆形信息。通过这种空间映射和边缘累加的方法,Hough 变换提取出了原始图像中的圆形信息。可以得到如下情况,这时并没有得到较好得效果,此时我们思考为啥为啥会出现下面这种情况呢?第五个参数为double类型的minDist(),为霍夫变换检测到的圆的圆心之间的最小距离,即让算法能明显区分的两个不同圆之间的最小距离。这个参数如果设置太小,多个相邻的圆可能被错误的检测成了一个重合的圆。反之,如果设置太大,某些圆就不能检测出来[8]。当适当改变后显示如下图所示。并且通过调整最小的可识别半径与最大可识别半径的数值之后,效果得到了极大的提升。别的的圆的标准也达到了我们的要求。

图十:为调整参数的参数

图十一:调整后的参数
3.2 定位算法
圆形物体在施工过程中可能发生变形, 且其位置也可能与设计不完全一致, 两者之间存在一定的差异。由于空间圆形物体的特征量 (圆心, 半径, 法方向等) 不能直接通过测量得到, 可能的方法是采集空间圆形物体上的一系列的点, 然后通过对这些点的数据进行处理得到该空间圆形物体的特征量。我们可以进行迭代法进行计算。因此需要我们设置目标函数。
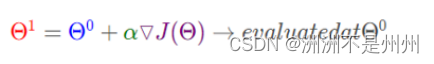
图十二:迭代公式
此公式的意义是:J是关于θ[10]的一个函数,我们当前所处的位置为θ0点,要从这个点走到J的最小值山底。首先我们先确定前进的方向,也就是梯度的反向,然后走一段距离的步长,也就是α,走完这个算法,就到达了θ1这个点。由此我们就能得到接下来的点,当θ的值不再发生变化时说明我们的迭代已经完成了。此时的值就是我们的目标值。
3.2.1 迭代算法
在上述的迭代公式中我们发现了欲求出θ值,首先需要定义J(θ)函数的表达式。我们利用初始圆心点与轮廓周围的点的距离写成一个距离表达公式。
在函数中我们可看到表达式中分别有a,b,r三个变量,为了求目标函数的最小值,我们分别对函数关于a,b,r三个变量进行求偏导如下公式所示。
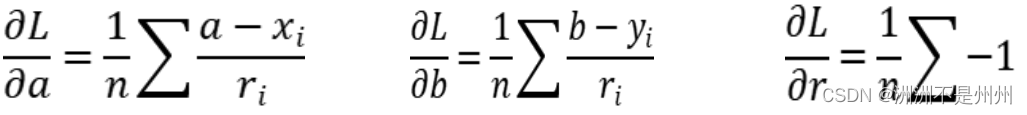图十四:偏导公式](https://img-blog.csdnimg.cn/20f80bd2509c409c831db9b59a2c02b1.png)
当知晓了以上的公式后,我们可以求出各个变量的迭代方程,具体公式如下:
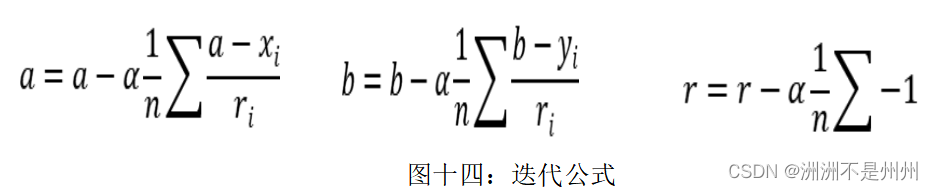
如上式所示,当知晓了迭代方程后,我们通过设定一个合适的初值,进行迭代,当迭代结束以后,说明我们已经到达了目标函数的最小点,由于我们的函数是凸函数,所以不存在局部最优解的这种情况,我们得到的点就是代价函数最小的情况,从而也就确定了a,b,r三个未知数的大小,从而也就完成了确定圆心的任务。难点就在于由于我们取初值的合适情况。如果设定的初值过小则迭代时间过长,如果过大的话也会如此,因此需要设置好比较合适的初值对于我们这个目标函数的求解有着比较大的影响。还有一个比较重要的因素就是迭代的步长了。如果迭代步长过小,会发现计算速度过慢,会在小范围内多次迭代,从而导致计算时间过长,会导致计算力的浪费。与之相反的就是迭代步长过大,这时候会导致迭代过度,跳跃了最小值点,而后在迭代的过程中我们发现,数值会越来越远离我们的最小值,此时函数的迭代情况出现了发散。会导致我们的计算结果出现问题。具体可有如下图示解释。
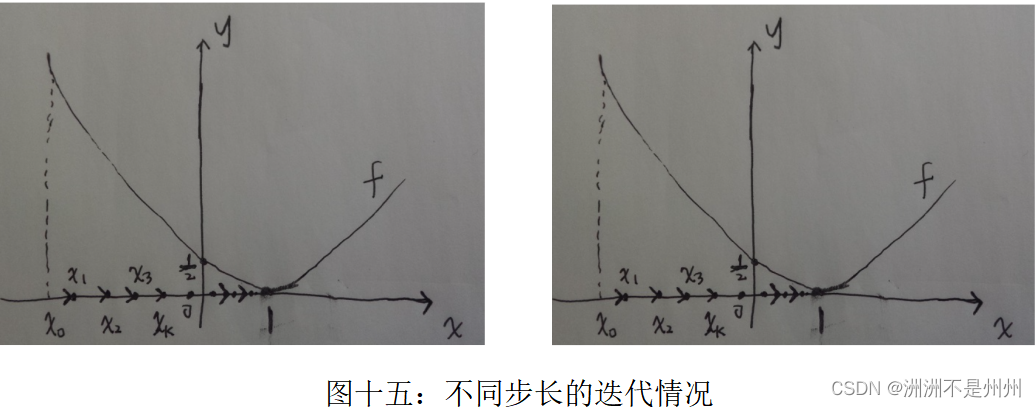
4.1 数据处理
由于干扰的轮廓点像素太多,我们需要识别圆的区域,并且对其进行数据处理与计算。首先需要大致定一个矩形框,把我们的圆框在里面,而后利用判断语句把框外的其他轮廓点去除掉,这样我们就能轻易地找出我们圆周围的像素点了。具体步骤如下:首先找到在图像中位于(477,81),(811,81),(477,381),(811,381)这四点,而后利用opencv中的图像操作画出矩形框,而后进行无关数据的滤除,极大减少了算力的浪费,节省了计算时间,极大提高了效率。处理后的照片如下图所示:


图十六:处理后能识别出的轮廓点
具体的数据如下所示:迭代求得的圆心坐标以及半径:圆心横坐标为x=650.796,圆心纵坐标为y=224.49,圆心半径:r=136.502。虽然跟我们之前设定的圆表达式:(x-654)2+(y-226)2=1422.但是我们发现还是存在一些误差的,在一般的工业生产中我们是可以实现自动抓取或则识别的功能的,但是一旦应用在精度高的场合时我们会发现这种结果是不太合适的。在接下来的实验中我发现是否是圆中的小人像素干扰到了我们的迭代算法呢?于是再接下来的实验中我将去除小人的轮廓像素,并计算其更新后的具体坐标数值。如下图所示:

图十七:滤除干扰信号后的结果
通过图像可得圆比之前拟合的好,其具体数值分别为x=652.96,圆心纵坐标为y=225.7,圆心半径:r=140.162由于滤除了图像中的一些干扰信号,我们圆的拟合效果变得更好了,说明我们的算法已经目标函数找的比较准确。但是由于环境的变化,我们经常对图像进行预处理的效果就会发生改变。所以该算法只能应用于类似的一些场景,适用场景不够广泛。改善方法就是利用深度学习去让机器自己去学习提高自身的识别准确率。
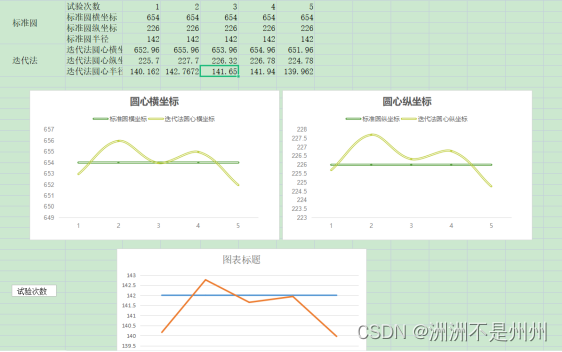
图十八:实验结果
五、深度学习介绍:
神经单元以层的方式组合,每一层的每个神经元和前一层、后一层的神经元连接,共分为输入层、输出层和隐藏层,三层连接形成一个神经网络。每层都会加上对应的权重,而且这些权重的大小也是不确定,根据梯度下降法后得到的权重,从而使我们的迭代最小值达到最小的情况,目前随着机器学习的普遍,计算机视觉用摄相机和计算机代替人眼对目标进行识别、跟踪和测量等机器视觉,并进一步做图形处理,使电脑最终呈现出来的图像是更有用的信息。随着人工智能的爆火,机器学习中深度学习因为深层次、中大火的机器算法[11],2012 年,在大规模图像数据集 ImageNet 上,神经网络方法取得了重大突破,准确率达到 84.7%。在 LFW 人脸识别评测权威数据库上,基于深度神经网络的人脸识别方法 DeepID 在 2014、2015 年分别达到准确率 99.15% 和 99.53%,远超人类识别的准确率97.53%。[12]这种技术在物种识别领域起到了很大的作用,大大减少了人为工作量为实现物种保护、物种养殖提供了巨大的帮助[26]。在论文中我们要求的是监督学习,也称为有教师学习,它对于一组给定输入可以提供出正确的输出结果,即期望输出, 神经网络根据实际输出与期望输出之间存在的差别来对连接权值等自身参数进行不断的调整,使实际输出无限接近于期望输出。其中反向传播最为重要,通过迭代,误差的反向传播是将输出误差以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。这种信号正向传播与误差反向传播的各层权值调整过程,是周而复始地进行。权值不断调整过程,也就是网络的学习训练过程。此过程一直进行到网络输出的误差减少到可以接受的程度,或进行到预先设定的学习次数为止。通用的模型如下:
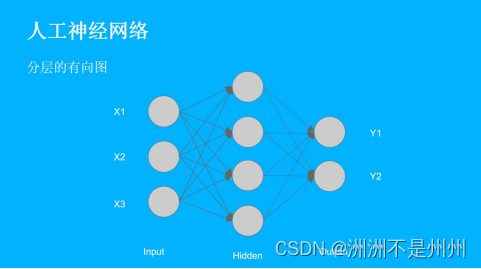
图十九:神经网络模型
接下来我们将确定一下激活函数,如果我们不运用激活函数的话,则输出信号将仅仅是一个简单的线性函数。线性函数一个一级多项式[13] 。现如今,线性方程是很容易解决的,但是它们的复杂性有限,并且从数据中学习复杂函数映射的能力更小。一个没有激活函数的神经网络将只不过是一个线性回归模型(Linear regression Model)罢了,它功率有限,并且大多数情况下执行得并不好。我们希望我们的神经网络不仅仅可以学习和计算线性函数,而且还要比这复杂得多。同样是因为没有激活函数,我们的神经网络将无法学习和模拟其他复杂类型的数据,例如图像、视频、音频、语音等。这就是为什么我们要使用人工神经网络技术,诸如深度学习(Deep learning),来理解一些复杂的事情,一些相互之间具有很多隐藏层的非线性问题,而这也可以帮助我们了解复杂的数据。目前比较普遍使用的是Sigmoid 激活函数:
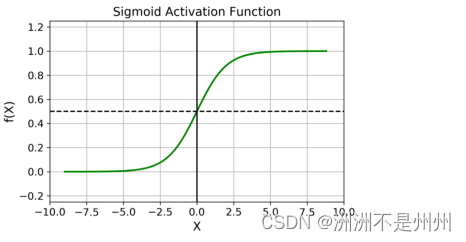
以下是使用Sigmoid 函数的理由:1:输出范围是 0 到 1。由于输出值限定在 0 到 1,因此它对每个神经元的输出进行了归一化;2:用于将预测概率作为输出的模型。由于概率的取值范围是 0 到 1,因此 Sigmoid 函数非常合适;3:梯度平滑,避免「跳跃」的输出值;函数是可微的。这意味着可以找到任意两个点的 sigmoid 曲线的斜率;4:明确的预测,即非常接近 1 或 0。
在接下来的时候将会认真学习有关深度学习的理论知识,并学习搭建模型,争取早日能应用到项目当中去。
总结:在牛顿迭代的算法下,基本能完成圆的检测并且能较好的客服图像的干扰,唯一的缺点就是如果图像预处理效果不到位,会使得轮廓像素点识别不清晰,导致识别失败。接下来打算利用深度学习去对图像进行监督学习,从而提高识别的准确率。
参考文献
[1]童胜杰,江明,焦传佳.一种改进工件边缘检测方法的研究[J].电子测量与仪器学报,2021,35(01):128-134.DOI:10.13382/j.jemi.B2003375.
[2]张敬峰. 基于卷积神经网络的圆检测方法研究[D].广西大学,2021.DOI:10.27034/d.cnki.ggxiu.2021.001458.
[3]龚昕,张楠.基于Hough变换的圆检测算法的改进[J].信息技术,2020,44(06):89-93+98.DOI:10.13274/j.cnki.hdzj.2020.06.020.
[4]潘国荣,谷川,施贵刚.空间圆形物体检测方法与数据处理[J].大地测量与地球动力学,2007(03):28-30.
[5]邓建清,黄劼,龙伟.一种孔系间距高精度的检测方法[J].组合机床与自动化加工技术,2004(01):59-60.
[6]卢晓冬,薛俊鹏,张启灿.基于圆心真实图像坐标计算的高精度相机标定方法[J].中国激光,2020,47(03):242-249.
[7] Warren S. Mcculloch, Walter Pitts. A Logical Calculus of the Ideas Immanent in Nervous Activity[J]. Bulletinof Mathematical Biology, 1943, 52(1–2):99-115.
[8] Hebb D.O. The organization of behavior. New York: Wiley,1949
[9] Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain.[J].Psychological Review, 65(6):386-408.
[10]A.M. Andrew. Marvin Minsky and Seymour Papert, Editors, Perceptrons, M.I.T. Press, Cambridge, Mass.(1969) 258 pp. 112s[J]. 1970(3):314-316.
[11] Hopfield, J. J. Neural networks and physical systems with emergent collective computational abilities.[J].Proceedings of the National Academy of Sciences of the United States of America, 79(8):2554-2558.
[12] Ackley D H , Hinton G E , Sejnowski T J . A Learning Algorithm for Boltzmann Machines[J]. Cognitive Science, 1985, 9(1):147-169.
[13] Rumelhart D E , Hinton G E , Williams R J . Learning Representations by Back Propagating Errors[J]. Nature,1986, 323(6088):533-536.