文章目录
- 前言
- 一、简单示例
- 二、gismo-3维IGA
- 3维程序中的几何模型
- 三、xml文件的理解
- 1、xml文件示例
- 2、gismo中二维示例文件-一个曲面(简单)
- 四、三维程序中xml文件的理解
- 三维几何模型
- 边界信息
- 五、三维程序运行
- 细化四次
- 细化5次
- 总结 #pic_center
前言
只是为方便学习,不做其他用途!
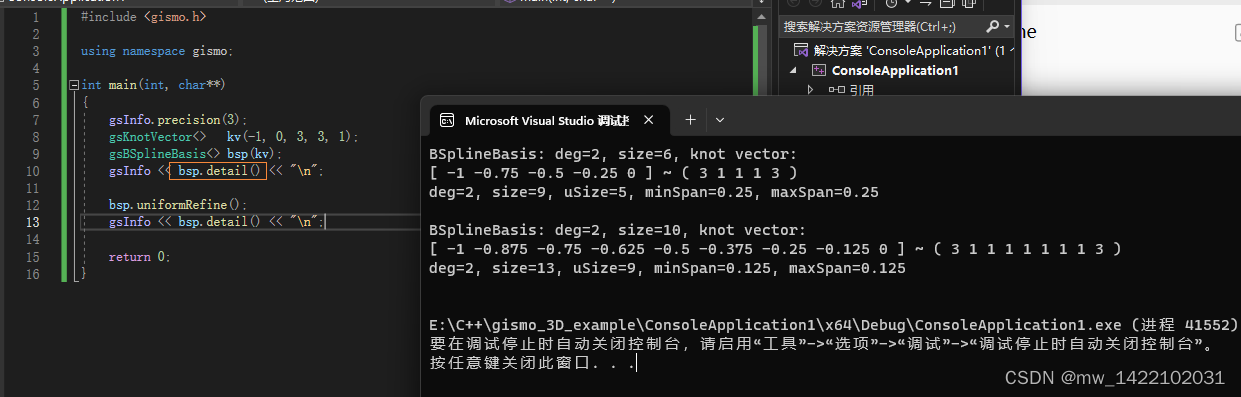
一、简单示例
参考网页 Tutorial 02: Geometry
#include <gismo.h>
using namespace gismo;
int main(int, char**)
{
gsInfo.precision(3);
gsKnotVector<> kv(-1, 0, 3, 3, 1);
gsBSplineBasis<> bsp(kv);
gsInfo << bsp.detail() << "\n";
bsp.uniformRefine();
gsInfo << bsp.detail() << "\n";
return 0;
}
二、gismo-3维IGA
运行代码需要配置好gismo环境
还需要将 terrific.xml 放在项目文件下,和cpp文件放在同一文件路径下

/// This is an example of using the linear elasticity solver on a 3D multi-patch geometry.
/// The problems is part of the EU project "Terrific".
///
/// Authors: O. Weeger (2012-1015, TU Kaiserslautern),
/// A.Shamanskiy (2016 - ...., TU Kaiserslautern)
#include <gismo.h>
#include <gsElasticity/gsElasticityAssembler.h>
#include <gsElasticity/gsWriteParaviewMultiPhysics.h>
#include <gsElasticity/gsGeoUtils.h>
using namespace gismo;
int main(int argc, char* argv[])
{
gsInfo << "Testing the linear elasticity solver in 3D-线弹性求解器的三维测试.\n";
//=============================================================//
// Input //
//=============================================================//
//std::string filename("terrific.xml");//初始数据文件
std::string filename("test.xml");//初始数据文件
real_t youngsModulus = 74e9;//杨氏模量
real_t poissonsRatio = 0.33;//泊松比
index_t numUniRef = 0;//节点插入数
index_t numDegElev = 0;//升阶次数
index_t numPlotPoints = 10000;//preview软件画图的点数量
// minimalistic user interface for terminal 终端最简用户界面
gsCmdLine cmd("Testing the linear elasticity solver in 3D.");// 定义一个gsCmdLine类 命名为cmd
cmd.addInt("r", "refine", "Number of uniform refinement application", numUniRef);
cmd.addInt("d", "degelev", "Number of degree elevation application", numDegElev);
cmd.addInt("p", "points", "Number of points to plot to Paraview", numPlotPoints);
try { cmd.getValues(argc, argv); } // 不太用看 不知道这个命令代表啥
catch (int rv) { return rv; }
//=====================================================================//
// Scanning geometry and creating bases:扫描几何和创建基函数 //
//=====================================================================//
// scanning geometry 扫描几何
gsMultiPatch<> geometry; // 定义一个多片
gsReadFile<>(filename, geometry);// 将plateWithHole.xml文件中的数据赋值给 geometry
// creating basis 生成基函数
gsMultiBasis<> basis(geometry);
for (index_t i = 0; i < numDegElev; ++i) // 升阶次数
basis.degreeElevate();
for (index_t i = 0; i < numUniRef; ++i) // k细化(节点插入)次数
basis.uniformRefine();
gsInfo << basis ;
//=====================================================================//
// Setting loads and boundary conditions 设置载荷和边界条件 //
//=====================================================================//
// source function, rhs 源函数?-解析解?
gsConstantFunction<> f(0., 0., 0., 3);
// surface load, neumann BC 黎曼边界对应载荷边界条件 荷载BC 力的边界条件
gsConstantFunction<> g(20e6, -14e6, 0, 3);
// boundary conditions 边界条件 黎曼边界对应载荷边界条件 dirichlete对应位移边界条件
gsBoundaryConditions<> bcInfo;
// Dirichlet BC are imposed separately for every component (coordinate) 对每个分量(坐标)分别施加 Dirichlet BC
for (index_t d = 0; d < 3; d++)
{
bcInfo.addCondition(0, boundary::back, condition_type::dirichlet, 0, d);
/* bcInfo.addCondition(1, boundary::back, condition_type::dirichlet, 0, d);
bcInfo.addCondition(2, boundary::south, condition_type::dirichlet, 0, d);*/
}
// Neumann BC are imposed as one function 将 Neumann BC 作为一个函数
bcInfo.addCondition(0, boundary::front, condition_type::neumann, &g);
//bcInfo.addCondition(14, boundary::north, condition_type::neumann, &g);
//=====================================================================//
// Assembling & solving //
//=====================================================================//
// creating assembler 创建刚度矩阵?
gsElasticityAssembler<real_t> assembler(geometry, basis, bcInfo, f);
assembler.options().setReal("YoungsModulus", youngsModulus);
assembler.options().setReal("PoissonsRatio", poissonsRatio);
assembler.options().setInt("DirichletValues", dirichlet::l2Projection);
gsInfo << "Assembling...\n";
gsStopwatch clock;
clock.restart();
assembler.assemble();
gsInfo << "Assembled a system with "
<< assembler.numDofs() << " dofs in " << clock.stop() << "s.\n";
gsInfo << "Solving...\n";
clock.restart();
#ifdef GISMO_WITH_PARDISO
gsSparseSolver<>::PardisoLDLT solver(assembler.matrix());
gsVector<> solVector = solver.solve(assembler.rhs());
gsInfo << "Solved the system with PardisoLDLT solver in " << clock.stop() << "s.\n";
#else
gsSparseSolver<>::SimplicialLDLT solver(assembler.matrix());
gsVector<> solVector = solver.solve(assembler.rhs());
gsInfo << "Solved the system with EigenLDLT solver in " << clock.stop() << "s.\n";
#endif
//=====================================================================//
// Output //
//=====================================================================//
// constructing solution as an IGA function
gsMultiPatch<> solution;
assembler.constructSolution(solVector, assembler.allFixedDofs(), solution);
// constructing stresses
gsPiecewiseFunction<> stresses;
assembler.constructCauchyStresses(solution, stresses, stress_components::von_mises);
if (numPlotPoints > 0)
{
// constructing an IGA field (geometry + solution)
gsField<> solutionField(assembler.patches(), solution);
gsField<> stressField(assembler.patches(), stresses, true);
// creating a container to plot all fields to one Paraview file
std::map<std::string, const gsField<>*> fields;
fields["Deformation"] = &solutionField;
fields["von Mises"] = &stressField;
gsWriteParaviewMultiPhysics(fields, "test_le", numPlotPoints);
gsInfo << "Open \"test_le.pvd\" in Paraview for visualization.\n";
}
return 0;
}
3维程序中的几何模型
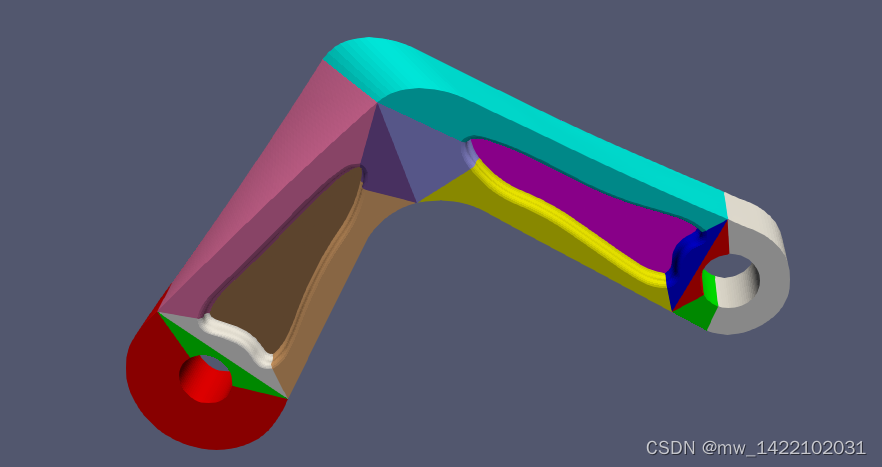

三、xml文件的理解
1、xml文件示例
网址https://gismo.github.io/Tutorial02.html


2、gismo中二维示例文件-一个曲面(简单)
可以参考之前的博客gismo中用等几何解决线弹性问题的程序示例来理解xml文件
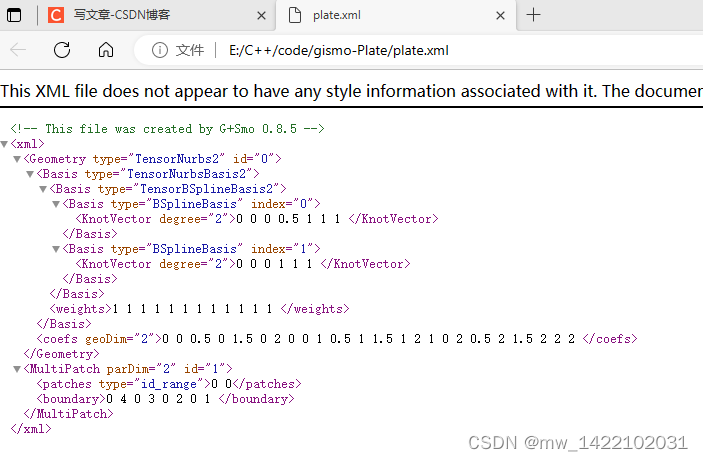
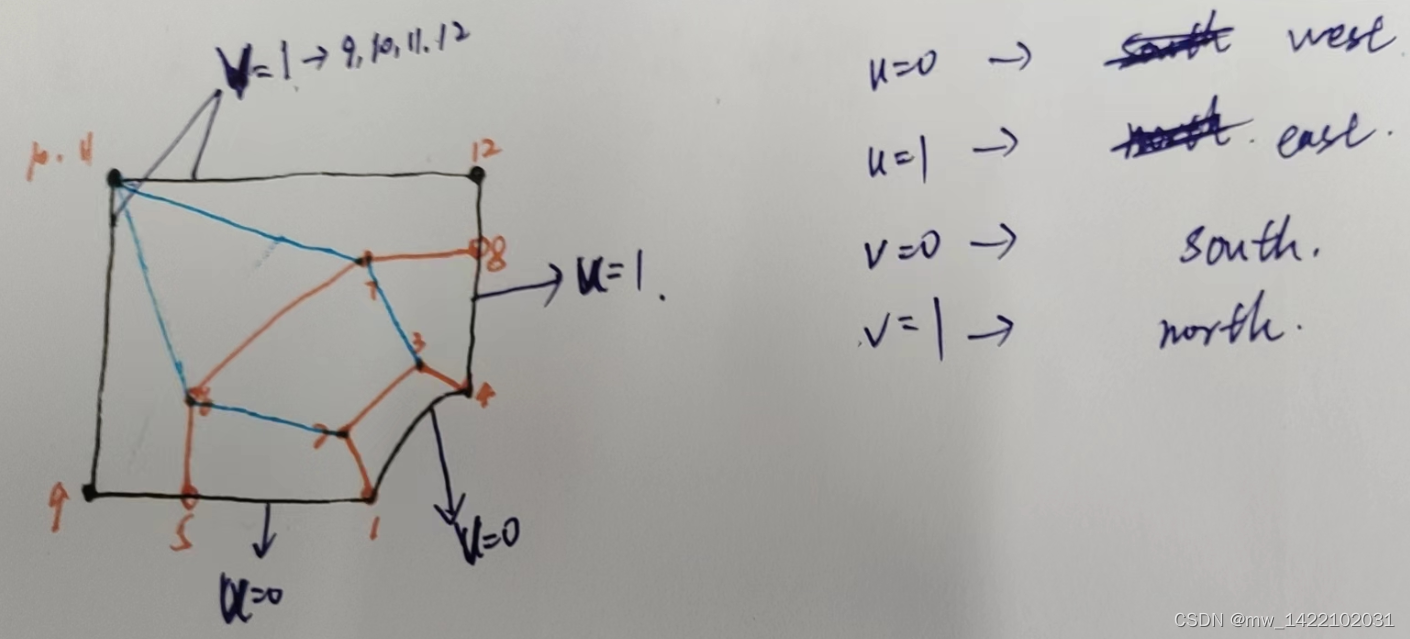

注: 一个平面没有 interfaces这一项
对 interfaces这一项 目前还没有理解
四、三维程序中xml文件的理解
三维几何模型

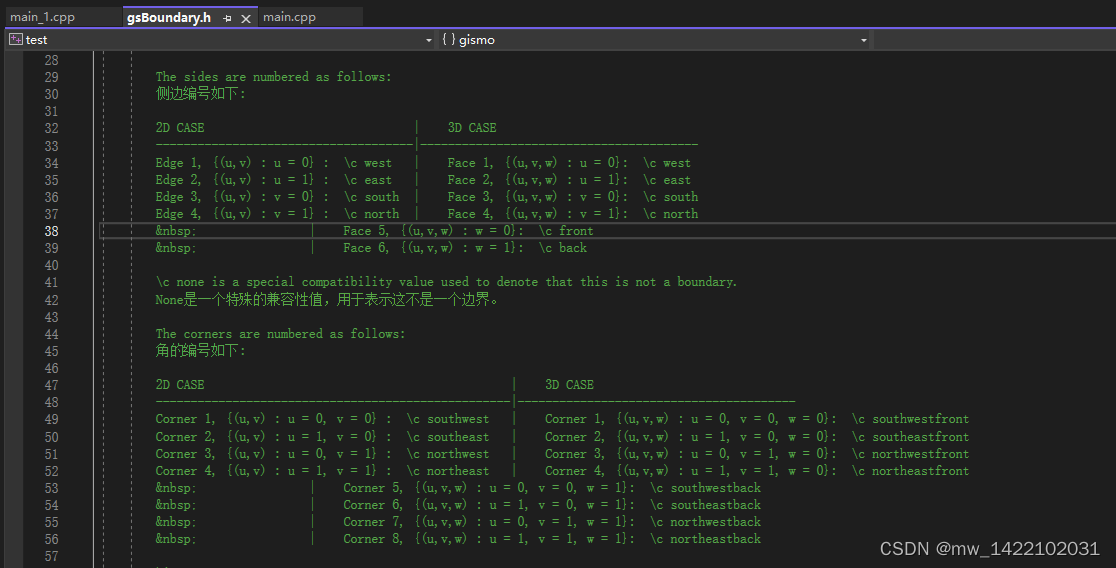
边界信息
给的示例文件中有15个体组装在一起



五、三维程序运行
细化四次
运行时间:14分钟
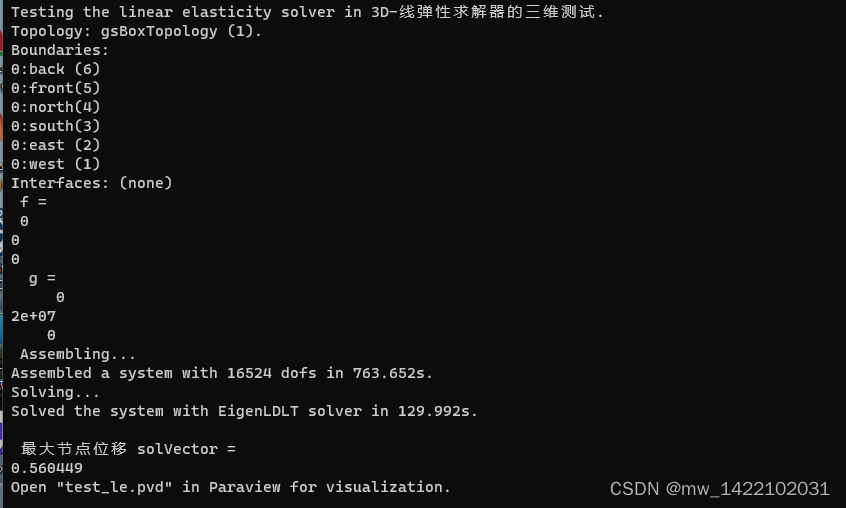
细化5次
运行时间:4.58h
组总刚:1.6h
解方程组:2.98h
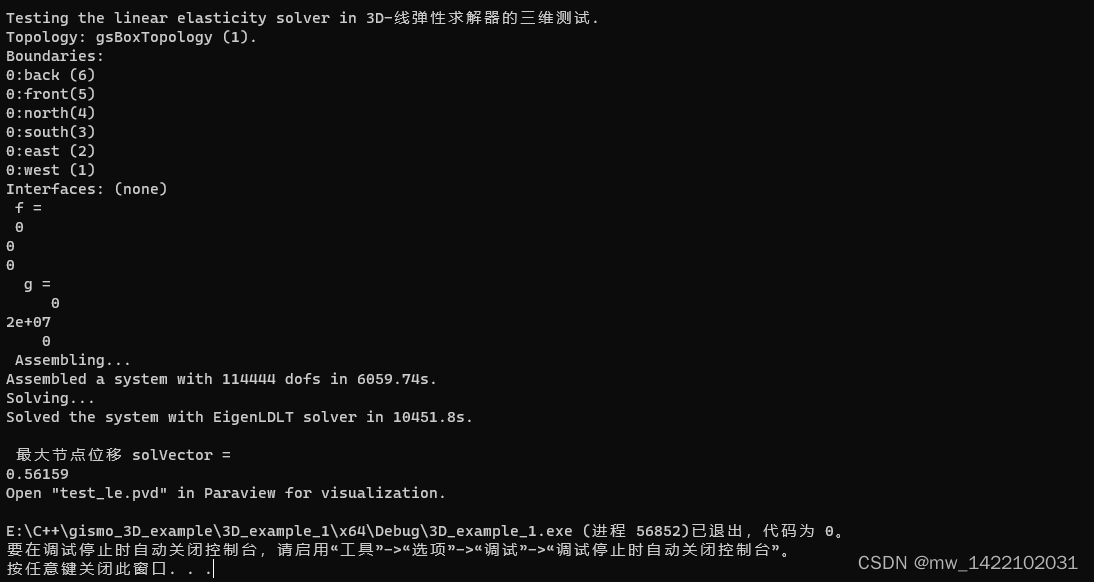
总结 #pic_center
空格 空格
:
| 二维数 |
| 1 |
| 1 |
| 1 |