地震动校正
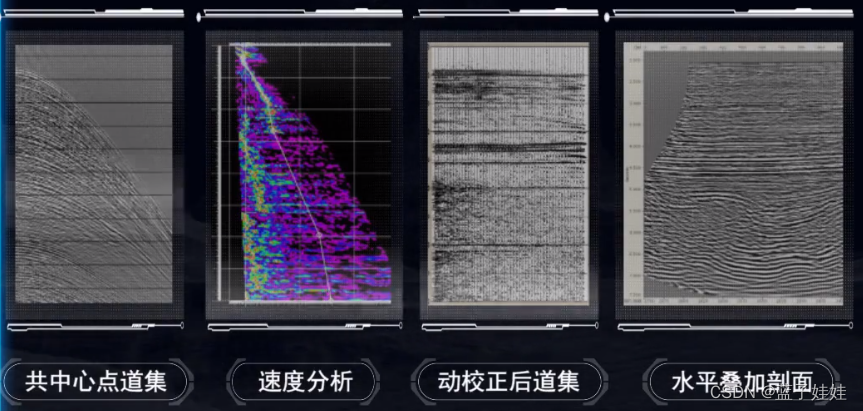
在地震资料数字处理过程中,速度分析,动校正和水平叠加三个处理内容是相互关联的。水平叠加是为了提高地震资料的信噪比,要想得到好的叠加效果,必须做好动校正。而做好动校正,需要进行准确的速度分析。只有利用准确的动校正速度消除共中心点道集中由于炮检距对于反射波旅行时的影响,才能得到高质量的水平叠加地震资料。
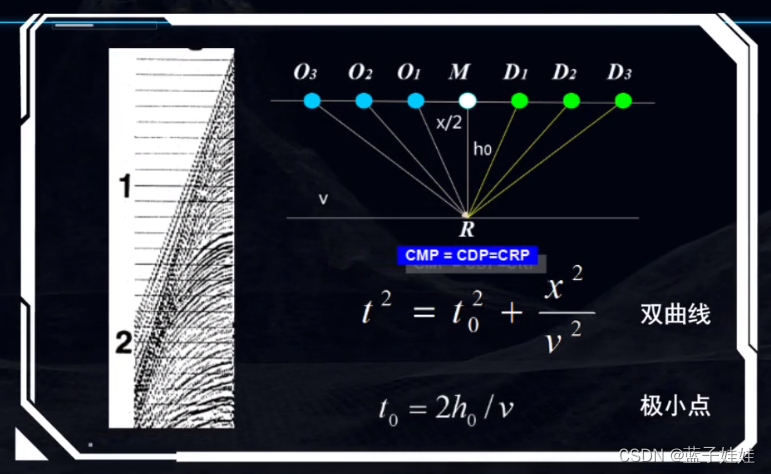
在一个水平界面的情况下,共中心点时距曲线方程是一条双曲线,在共中点道集记录上,双曲线的极小点在中心点的正下方。
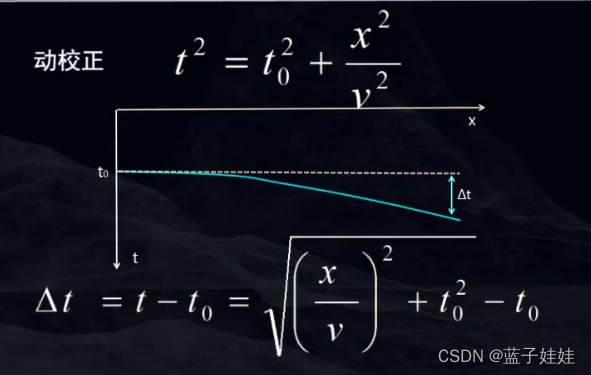
在共中心点道集中,反射波到达时间中包含有炮检距引起的正常时差(NMO),从观测时间中去掉或者把非零炮检距地震波的反射时间校正为零炮检距的反射时间 t 0 t_0 t0 的过程称为动校正,也称为正常时差校正,或者为NMO校正。正常时差NMO也称为动校正量。
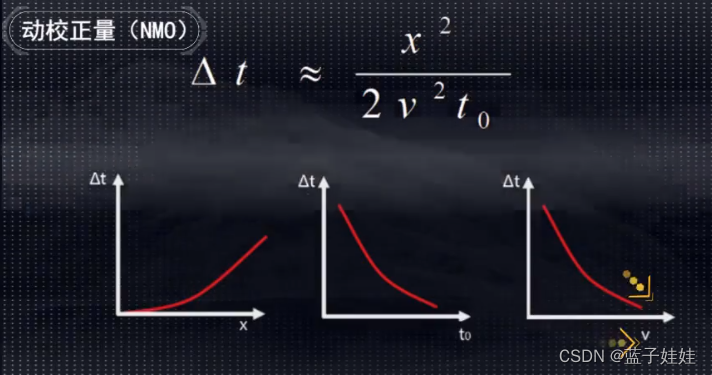
从动校正 Δ t \Delta t Δt 的近似公式上可以看到,随着炮检距 x x x 的增加, Δ t \Delta t Δt 是增加的。随着 t 0 t_0 t0 的增加, Δ t \Delta t Δt 是减小的。随着 v v v 的增加, Δ t \Delta t Δt 也是减小的。炮检距 x x x 是已知的, t 0 t_0 t0 也是已知的,利用速度分析可以求出动校正速度。
对于任意一道地震记录来说,深浅层反射波的动校正量不同,浅层波组的动校正量大于深层波组的动校正量,这就是动校正中“动”的含义。合适的动校正量取决于动校正速度函数,当动校正量合适时,能够把共反射点道集内反射波旅行时间校正为双程垂直旅行时间实现同相位叠加。
从共中心点反射波时距曲线中减去动校正量的过程称为动校正。动校正后,时距曲线就变成了直线,即可同向叠加,能够起到提高信噪比的作用。
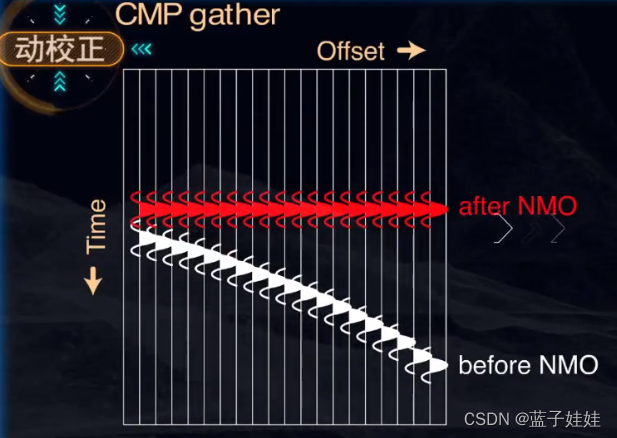
在水平层状地层情况下,共中心点反射波的时距曲线仍然是双曲线,该方程和一个水平界面情况下的形式是一样的,只是速度 v v v 用均方根速度 v r m v_{rm} vrm 表示。
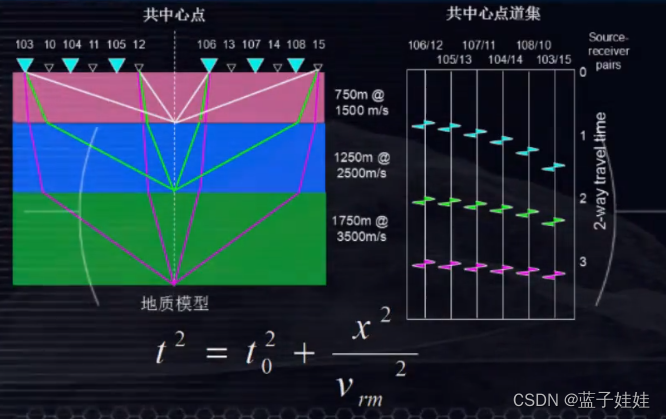
共中心点道集记录动校正后时距曲线拉平,就可以进行地震水平叠加,叠加成为一道起到提高信噪比的作用。多个共中心点道集记录重复上面的工作,就可以得到水平叠加地震剖面。
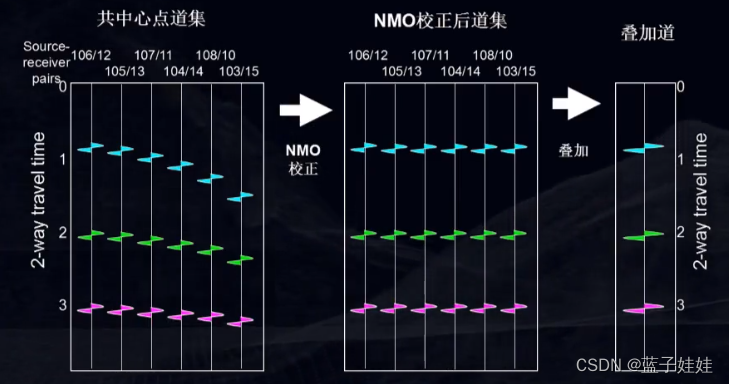
下图展示了一个共中心点道集经过动校正后叠加成为一道的过程。动校正处理主要涉及两个方面的内容,一是精确地计算动校正量,二是进行动校正时尽量减少波形畸变,力求动校正后精确地保持地震波波形。
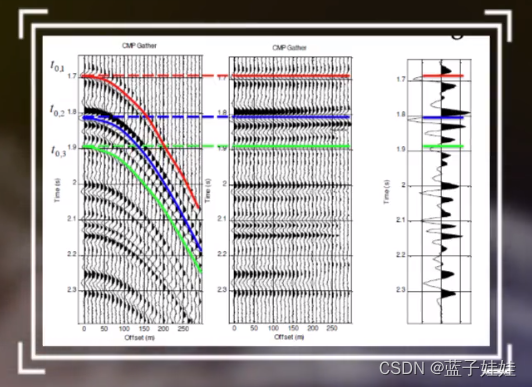
如下图所示,实际的共中心点道集动校正前是一系列的双曲线,动校正后双曲线被拉平,但是浅层的记录被严重拉伸畸变,而且畸变后的地震波频率变低。
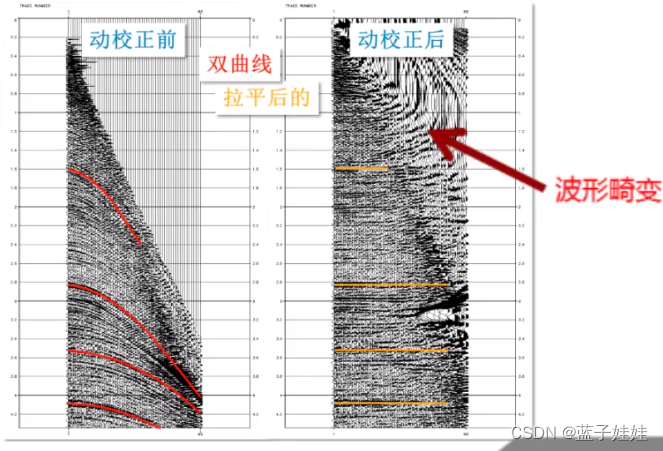
动校正的拉伸畸变是动校正过程的正常现象,由于NMO值随着炮检距的增加而增加,随着 t 0 t_0 t0 时间的增加而减小,因此子波顶部的校正量大于底部,引起地震子波的畸变。在浅层和大炮检距情况下,拉伸畸变最严重。拉伸畸变系数等于拉伸前后的变换量比上拉伸前的长度。NMO校正前后的频率差 Δ f \Delta f Δf 与校正前的频率 f f f 之比近似等于动校正量 Δ t \Delta t Δt 与 t 0 t_0 t0 之比。
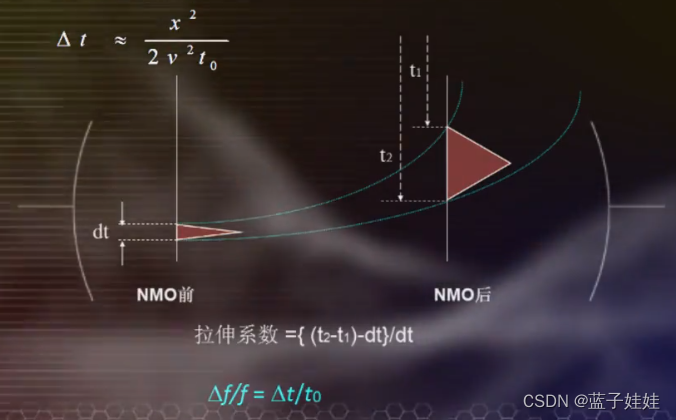
拉伸畸变后的波如果参与叠加会影响叠加效果,通常的做法是切除拉伸畸变部分,再做水平叠加。

如果地下界面是倾斜的情况下,共中心点反射波时距曲线仍然也可以看成是近似的双曲线,但是实际曲线中的速度是等效速度。把倾斜界面等效为水平界面情况下,共中心点反射波时距曲线中所用的速度就是等效速度,等效速度与地层倾角有关。
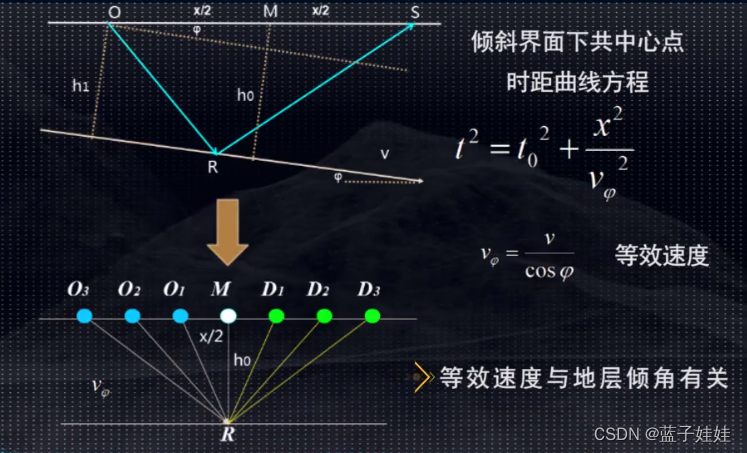
可以将倾斜界面情况下共中心点反射波时距曲线方程改写为如下图所示,公式前两部分代表正常时差 (NMO),后一部分代表倾角时差 (DMO)。

因此,倾斜界面情况下,NMO 校正后反射波的时距曲线是校不直的,如果再进行一次倾角时差校正 (DMO),反射波时距曲线就可以进行水平叠加。
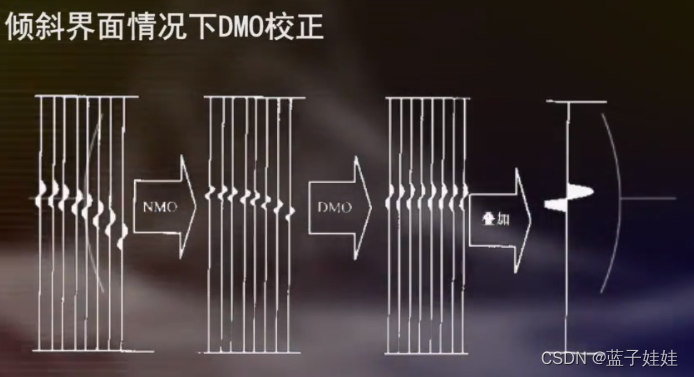
在更复杂的地下介质情况下,反射波时距曲线本身就不是双曲线了,需要引入高阶动校正的概念。
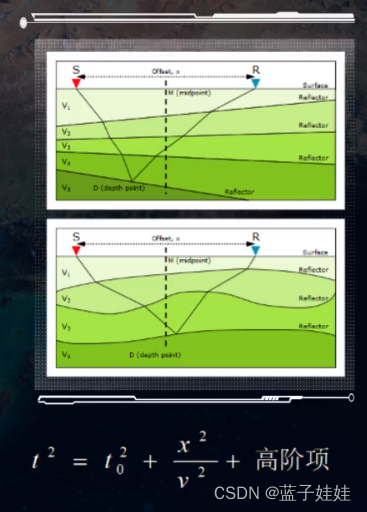
共中心点反射波时距曲线可以近似写成炮检距的偶次方乘以多个系数之和。 C 0 C_0 C0 表示 t 0 t_0 t0, C 1 C_1 C1 与均方根速度有关, C 2 C_2 C2 与地下介质的各向异性参数有关。保留时距曲线右边的前三项进行的动校正成为四阶动校正。
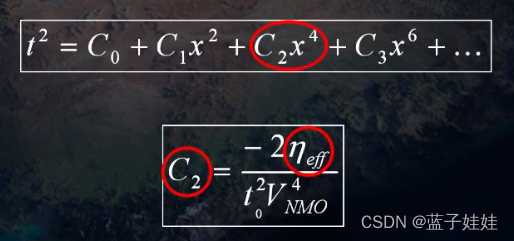
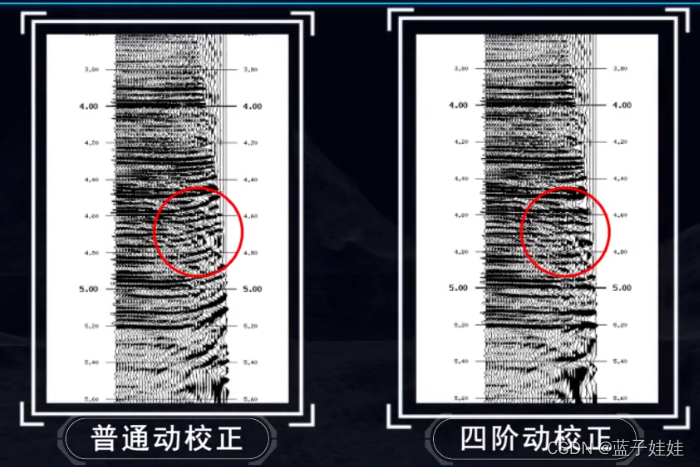
在排列长度不大的情况下,二阶动校正和四阶动校正差别不大。
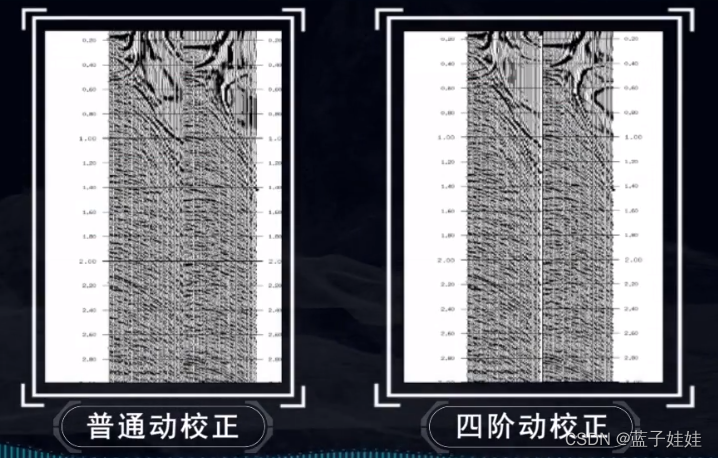
在排列长度较大的情况下,二阶动校正和四阶动校正差别较大。四阶动校正可以让大炮检距的地震道拉直。